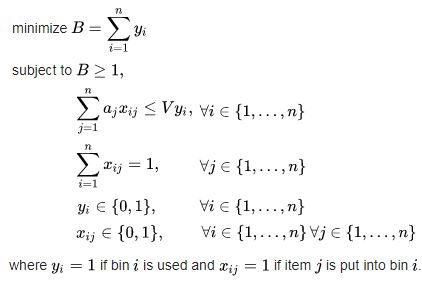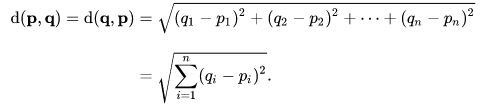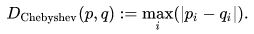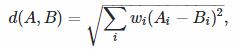Bucket-brigade

overview

This project contains two parts:

Simulation of the picking process.
Heuristic for optimization of batching and ordering.

Picking Process

Each picker have to pick a list of items from the pick faces. The list of items referred as a batch.

The moving of the pickers is discrete and dependent on their direction. The last picker picks till he finish to pick all the items in his batch. When he finish he starts to walk backwards until he "meet" the picker behind him, he transfer the batch to the last picker, and walks backwards and so on...

The process ends when all the batches have been picked.

The moving and item picking durations are sampled from a normal distributions with different means and variances which depends on the picker. So the process is Stochastic.

Input - List of orders

Challenge - Batching the orders and ordering the batches

Objective - Minimization of the picking time.

Heuristic

The suggested heuristic divides the problem into two classic, well studied combinatorial optimization problems:

Batching - Bin Packing problem

The task of batching can be solved optimally with the well known Bin packing problem.

The problem formulated in Wikipedia as:

In the context of batching the bins represents batches, subject to the maximal number of items that a picker can pick on a single batch.

the problem formulated on python and solved as a linear programming problem. with a timeout of 5 minutes.

Batch Ordering - Traveling Salesman problem (TSP)

TSP is probably one of the most famous problems, however it's relation to the batch ordering problem is not trivial.

The intuition to use TSP came from the assumption that: subsequent batches should be similar as much as possible.

There is no proof to this assumption, but it sounds reasonable since "gaps" between subsequent batches may lead to "gaps" between pickers - greater walking distance..

So the idea is to model each batch as a city in the TSP problem and each pick face as a dimension.

It will produce n-dimensional TSP problem, we can also relax the constraint that the route should be cyclic, since it doesn't matter here.

Distance Metrics

The most intuitive is the euclidean distance:

Since the meaning of distance in this context is tentative, we are not limited to the euclidean distance...

Better understanding of the dynamics in the picking process may lead to choose different distance metrics, like Chebyshev distance:

which will take into account only the dimension (pick face) with the greatest difference or the "bottle neck" between two batches.

Less "radical" metric could be a weighted euclidean metric:

By tuning the set of weights, different pick faces can be prioritized.

benchmark

pick faces	pickers	capacity	data	random order	euclidean	chebyshev
6	2	60	a	80.8458	86.7586	87.3944
6	2	90	a	65.5462	62.0748	64.0948
6	2	60	b	68.698	70.787	67.5055
6	2	90	b	52.5133	51.8276	50.5389
10	2	100	a	423.1702	426.9223	423.4411
10	3	100	a	248.6059	260.6872	251.6718
10	2	150	a	388.2158	379.0371	382.8692
10	3	150	a	237.7211	235.1055	228.3656
10	2	100	b	379.7337	376.8501	379.9041
10	3	100	b	254.0586	249.6524	253.8969
10	2	150	b	348.0816	339.3629	345.4822
10	3	150	b	257.2213	251.1654	250.7208
25	4	150	a	643.5016	627.7213	630.4875
25	3	150	a	788.5648	762.4215	768.6529
25	4	200	a	600.6101	591.4878	588.1468
25	3	200	a	762.6971	760.5763	755.4764
25	4	150	b	543.3693	539.8765	541.7146
25	3	150	b	813.4865	807.4245	806.1265
25	4	200	b	520.5971	517.9854	519.8875
25	3	200	b	742.7545	738.7964	730.9854

running the code

To install all the dependencies, run the following command:

pip install -r requirements.txt

Then run interface.py , the following menu will appear:

0 - all
1 - 6 pick-faces, 2 pickers, 60 items capacity, data a
2 - 6 pick-faces, 2 pickers, 90 items capacity, data a
3 - 6 pick-faces, 2 pickers, 60 items capacity, data b
4 - 6 pick-faces, 2 pickers, 90 items capacity, data b
5 - 10 pick-faces, 2 pickers, 100 items capacity, data a
6 - 10 pick-faces, 3 pickers, 100 items capacity, data a
7 - 10 pick-faces, 2 pickers, 150 items capacity, data a
8 - 10 pick-faces, 3 pickers, 150 items capacity, data a
9 - 10 pick-faces, 2 pickers, 100 items capacity, data b
10 - 10 pick-faces, 3 pickers, 100 items capacity, data b
11 - 10 pick-faces, 2 pickers, 150 items capacity, data b
12 - 10 pick-faces, 3 pickers, 150 items capacity, data b
13 - 25 pick-faces, 4 pickers, 150 items capacity, data a
14 - 25 pick-faces, 3 pickers, 150 items capacity, data a
15 - 25 pick-faces, 4 pickers, 200 items capacity, data a
16 - 25 pick-faces, 3 pickers, 200 items capacity, data a
17 - 25 pick-faces, 4 pickers, 150 items capacity, data b
18 - 25 pick-faces, 3 pickers, 150 items capacity, data b
19 - 25 pick-faces, 4 pickers, 200 items capacity, data b
20 - 25 pick-faces, 3 pickers, 200 items capacity, data b
choose config: (0,2..,20). x to exit

note: since the heuristic is compound of computationally hard problems, it's recommended to run the 25 pick faces configurations on a computer with at least 16GB RAM

Choose the configuration by entering it's number (0-20)

Interpreting the results

The results are looking like:

$@==################################################################################==@$
Vector [2, 7, 1, 1, 3, 0] is packed in bin 5.
Vector [0, 5, 3, 0, 1, 4] is packed in bin 2.
Vector [1, 2, 7, 6, 2, 0] is packed in bin 1.
Vector [0, 0, 0, 1, 5, 1] is packed in bin 1.
Vector [0, 4, 2, 0, 1, 7] is packed in bin 2.
Vector [0, 1, 3, 5, 1, 7] is packed in bin 6.
Vector [4, 8, 6, 1, 7, 7] is packed in bin 2.
Vector [1, 6, 2, 0, 4, 6] is packed in bin 6.
Vector [4, 0, 6, 7, 0, 6] is packed in bin 6.
Vector [8, 7, 1, 2, 0, 7] is packed in bin 11.
Vector [5, 5, 0, 7, 0, 6] is packed in bin 5.
Vector [1, 1, 0, 5, 0, 1] is packed in bin 1.
Vector [7, 4, 1, 2, 2, 0] is packed in bin 1.
Vector [0, 5, 4, 0, 0, 2] is packed in bin 1.
Vector [0, 0, 8, 1, 3, 5] is packed in bin 13.
Vector [8, 2, 4, 0, 7, 5] is packed in bin 13.
Vector [2, 2, 3, 3, 1, 6] is packed in bin 13.
Vector [1, 5, 0, 2, 0, 0] is packed in bin 11.
Vector [5, 6, 0, 4, 0, 5] is packed in bin 5.
Vector [8, 6, 2, 3, 7, 1] is packed in bin 11.
bin 1: [ 9 12 12 14  9  4]
bin 2: [ 4 17 11  1  9 18]
bin 5: [12 18  1 12  3 11]
bin 6: [ 5  7 11 12  5 19]
bin 11: [17 18  3  7  7  8]
bin 13: [10  4 15  4 11 16]
batch 0: [ 9 12 12 14  9  4] sum: 60
batch 1: [12 18  1 12  3 11] sum: 57
batch 2: [17 18  3  7  7  8] sum: 60
batch 3: [ 4 17 11  1  9 18] sum: 60
batch 4: [10  4 15  4 11 16] sum: 60
batch 5: [ 5  7 11 12  5 19] sum: 59
$@==#### 6 pick-faces, 2 pickers, 60 items capacity, data a -> 93.8078 seconds.####==@$
$@==################################################################################==@$

The lines which starts with Vector says to which bin (batch) each order related. the bins id can take different numbers, they mean nothing at that stage.
The lines which starts with bin represents the actual batches and the number of items that should be picked on each pick face.
The lines which starts with batch are ordered.
The last line describes the configuration and the result of the simulation.

eeddaann / Bucket-brigade