$\lambda$ - интенсивность входного потока,
$\mu$ - интенсивность обслуживания
$k$ - число серверов,
$0$ - размер очереди,
Модель без очереди, если пришедшее требование застает все сервера занятыми, то требование получает отказ в обслуживании и считается потерянным
Вероятностное пространство
$ \mathcal{F=2^{\Omega}}$
$ \Omega = { \omega = (\omega_1, \omega_2, \omega_3,...) } $, где $ \omega_i \in {0, 1, 2,\cdots,k } $ - состояние системы (количество требований в системе)
$ P(\omega_{i+1} = \xi_{i+1} | \omega_{i} = \xi_{i}, \omega_{i-1} = \xi_{i-1}, ... , \omega_{1} = \xi_{1}) = P(\omega_{i+1} = \xi_{i+1} | \omega_{i} = \xi_{i})$
$P_0(1, 0, 0, ...) $
$ S = { 1, ..., k} $
Пусть $ X \sim exp(\lambda)$, $ Y \sim exp(\mu) $
Тогда $ P(X<Y) = \int_{0}^{\infty}P(X < Y | Y = y) \cdot k \mu e^{-yk\mu } dy ;; (; = ;) ;;$
= $ 1 - e^{-y \lambda} \Rightarrow P(x < y) = \int_{0}^{\infty}(1 - e^{-y \lambda}) k\mu \cdot e^{-y k\mu} = $
= $ \int_{0}^{\infty} k\mu e^{-yk \mu} dy - \mu k\int_{0}^{\infty} e^{-y (\lambda + k\mu)} dy = $
$-e^{-y k\mu} |_0^{\infty} - \frac{k\mu}{\lambda + k\mu} \cdot e^{-y ( \lambda + k\mu) } |_0^{\infty} = \frac{ \lambda }{\lambda + k\mu}$
(т. к $\;\; -e^{-y k\mu} |_0^{\infty} \; = \;1$ и $\;\; e^{-y (\lambda + k\mu) } |_0^{\infty} \;=\; 1) $
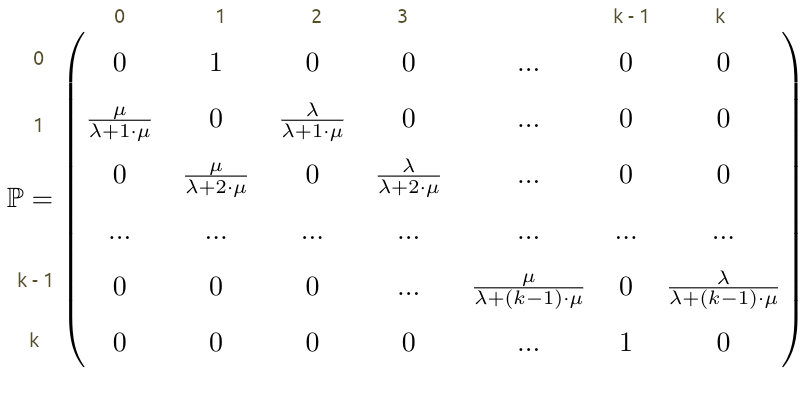
(1)
$ \lambda p_0 = \mu p_1 $
$ (\lambda + \mu) p_1 = 2 \mu p_2 + \lambda p_0 $
$ (\lambda + 2 \mu) p_2 = 3 \mu p_3 + \lambda p_1 $
$ ... $
$ (\lambda + i \mu) p_i = (i+1) \mu p_i + \lambda p_{i-1} $
$ k \lambda p_k = \lambda p_{k-1}$
Откуда
$ \lambda p_0 = \mu p_1 $
$ \lambda p_1 = 2 \mu p_2 $
$ \lambda p_2 = 3 \mu p_3 $
$ ... $
$ \lambda p_{k-1} = k \mu p_k $
Откуда:
(2)
$ p_1 = \frac{\lambda}{\mu}p_0, ; p_2 = \frac{\lambda}{2 \mu} p_1 = \frac{1}{2} \frac{\lambda}{\mu}^2 p_0 ; ... $
$ p_n = \frac{\lambda}{k \mu}p_{k-1} = \frac{1}{k!}\frac{\lambda}{\mu}^{k}p_0 $
$ p_0 + p_1 + p_2 + ... + p_k = 1 $
$ p_0( 1 + \frac{\lambda}{\mu} + ... \frac{\lambda^k}{k! \mu^k }) = 1 \Rightarrow p_0 = (1 + \frac{\lambda}{\mu} + ... + \frac{\lambda^k}{k! \mu^k})^-1$
(1) и (2) - формулы финальных вероятностей (формулы Эрланга)
$ \frac{\lambda}{\mu} = \rho $ - среднее число заявок / среднее время обслуживания одной заявки
Финальные вероятности:
$ \lambda \neq \mu: ;$
$ p_1 = \rho p_0, \; p_2 = \frac{\rho^2}{2!}p_0, ..., \; p_k = \frac{\rho^k}{k!}p_0$
$ \lambda = \mu: ;$
$ p_1 = p_0, \; p_2 = \frac{p_0}{2}, ..., \; p_k = \frac{p_0}{k!}$
1) Среднее время обслуживания требования сервером =
$ \frac{1}{\mu}$
2) Вероятность отказа $p_{\text{отк}}$ =
$$ p_k = \frac{\rho^k}{k!}p_0 $$
3) Среднее число занятных серверов ($ k_{ср}$)
можно найтие как матожидание:
$k_{ср}$ = $E(0 \cdot p_0 + 1 \cdot p_1 + ... + k \cdot p_k)$
или через абсолютную пропускную способность $A$:
$k_{ср} = \frac{A}{\mu} = \rho ( 1 - \frac{\rho^k}{k!}p_0)$
4) Абсолютная пропускная способность A (среднее число заявок, обслуживаемых в единицу времени)
$A = \lambda \cdot Q = \lambda( 1 - \frac{\rho^k}{k!}p_0) $
5) Отностительная пропускная способность $Q$ (вероятность принятие в обслуживание)
$Q = 1 - p_{\text{отк}} = 1 - \frac{\rho^k}{k!}p_0 $
6) Вероятность простоя системы: $p_n = p_0 $
import numpy as np
import matplotlib.pyplot as plt
import mathdef simulate(mean_arrival_rate, mean_departure_rate, number_of_servers, end_time):
timeline = []
active_servers = 0
current_time = np.random.exponential(mean_arrival_rate)
while current_time <= end_time:
timeline.append({'event': 'arrival', 'served': None, 'time': current_time, 'active_servers': 0, 'time_in_state': 0})
current_time += np.random.exponential(mean_arrival_rate)
current_time = 0
for point in timeline:
current_time = point['time']
if point['event'] == 'arrival':
if active_servers < number_of_servers:
point['served'] = True
active_servers+=1
point['active_servers'] = active_servers
departure_point = {'event': 'departure', 'time': current_time+np.random.exponential(mean_departure_rate), 'time_in_state': 0}
for i in range(len(timeline)-1, -1, -1):
if timeline[i]['time'] < departure_point['time']:
timeline.insert(i+1, departure_point)
break
else:
point['served'] = False
elif point['event'] == 'departure':
active_servers-=1
point['active_servers'] = active_servers
for i in range(len(timeline)-1):
timeline[i]['time_in_state'] = timeline[i+1]['time'] - timeline[i]['time']
return timelinedef stationary_probabilities(timeline, num_servers):
states_time = [0 for i in range(num_servers+1)]
for event in timeline:
states_time[event['active_servers']]+=event['time_in_state']
return [states_time[i]/res[-1]['time'] for i in range(len(states_time))]def reject_probability(timeline):
arrivals = [event for event in timeline if event['event']=='arrival']
rejected = [arrival for arrival in arrivals if arrival['served']==False]
return len(rejected)/len(arrivals)def relative_bandwith(timeline):
return 1 - reject_probability(timeline)def absolute_bandwith(timeline):
arrivals = [event for event in timeline if event['event']=='arrival']
served = [arrival for arrival in arrivals if arrival['served']==True]
return len(served)/timeline[-1]['time']def average_load(timeline, mu_):
return absolute_bandwith(timeline)/mu_def downtime_probability(timeline):
no_clients = [event for event in timeline if event['active_servers']==0]
downtime = sum([event['time_in_state'] for event in no_clients])
return downtime/timeline[-1]['time']def draw_load_plot(arrival_rate, departure_rate, servers, end_time=250):
timeline = simulate(arrival_rate, departure_rate, servers, end_time)
plt.figure(figsize=(20,5))
plt.grid()
plt.axis([0, end_time, 0, servers])
plt.title(label="График загруженности серверов при lambda={}, mu={}, {} servers".format(np.round(1/arrival_rate, 2), np.round(1/departure_rate, 2), servers))
ax = [point['time'] for point in timeline]
ax.insert(0, 0)
ay = [point['active_servers'] for point in timeline]
ay.insert(0, 0)
plt.plot(ax, ay)
plt.show()def draw_rejection_plot(mean_departure_rate, servers):
mean_arrival_rate = list(range(1,30))
lambda_ = [1/x for x in mean_arrival_rate]
rejection_probabilities = []
for x in mean_arrival_rate:
res = simulate(x, mean_departure_rate, servers, 10000)
rejection_probabilities.append(reject_probability(res))
plt.title(label='График роста вероятности отказа с ростом lambda; mu={}, {} servers'.format(1/mean_departure_rate, servers))
plt.plot(lambda_, rejection_probabilities)
plt.show()def draw_rel_bandwith_plot(mean_departure_rate, servers):
mean_arrival_rate = list(range(1,30))
lambda_ = [1/x for x in mean_arrival_rate]
rel_bandwiths = []
for x in mean_arrival_rate:
res = simulate(x, mean_departure_rate, servers, 10000)
rel_bandwiths.append(relative_bandwith(res))
plt.title(label='График падения относительной пропускной способности с ростом lambda; mu={}, {} servers'.format(1/mean_departure_rate, servers))
plt.plot(lambda_, rel_bandwiths)
plt.show()def draw_downtime_plot(mean_departure_rate, servers):
mean_arrival_rate = list(range(1,30))
lambda_ = [1/x for x in mean_arrival_rate]
downtime = []
for x in mean_arrival_rate:
res = simulate(x, mean_departure_rate, servers, 10000)
downtime.append(downtime_probability(res))
plt.title(label='График среднего времени простоя с ростом lambda; mu={}, {} servers'.format(1/mean_departure_rate, servers))
plt.plot(lambda_, downtime)
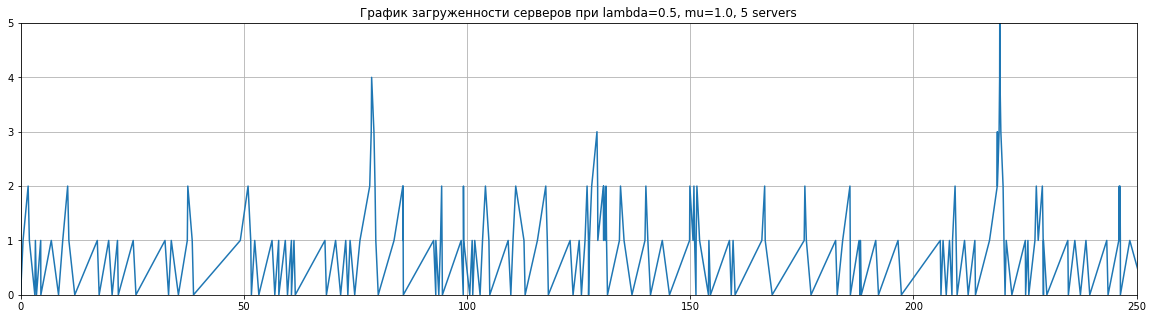
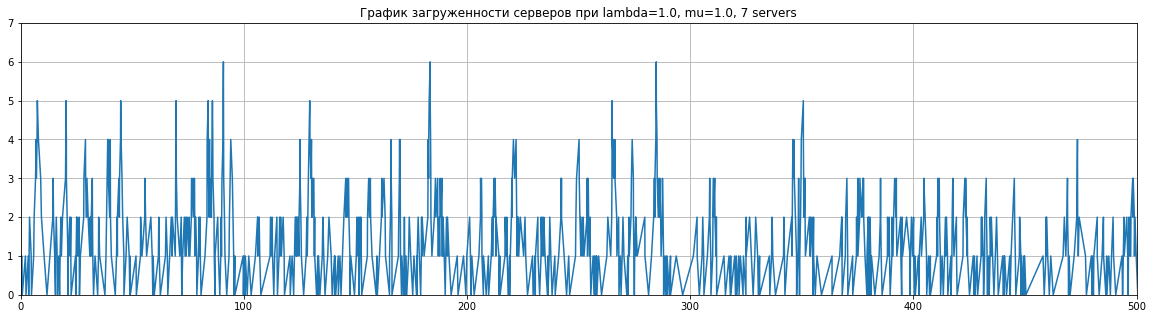
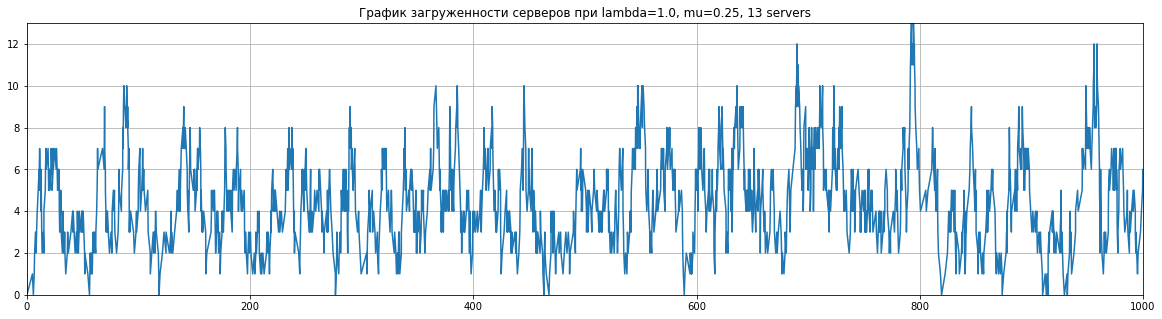
plt.show()draw_load_plot(2, 1, 5)draw_load_plot(1, 1, 7, 500)draw_load_plot(1, 4, 13, 1000)Видно, что если при росте $\lambda$ относительно $\mu$ нам требуется больше серверов для песперебойной работы.
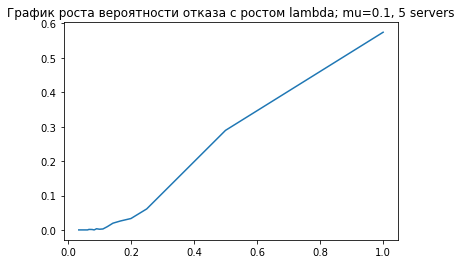
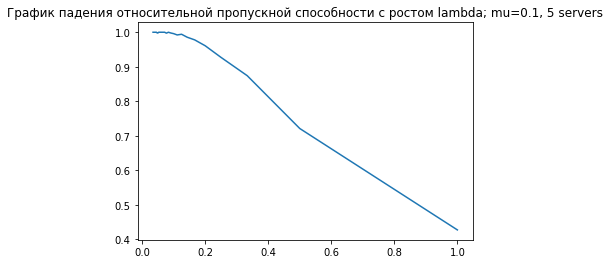
draw_rejection_plot(10, 5)draw_rel_bandwith_plot(10, 5)На этих двух графиках видно, как с ростом $\lambda$ пяти серверов становится недостаточно, и приходится отказывать заявкам.
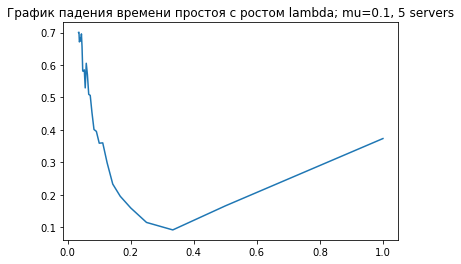
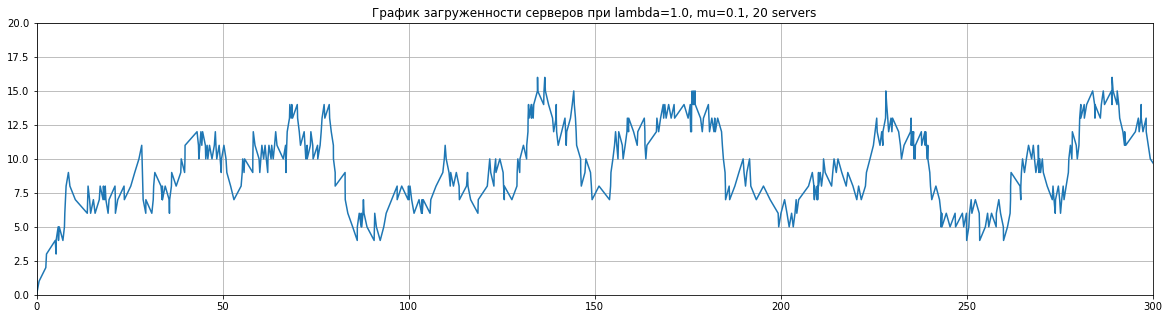
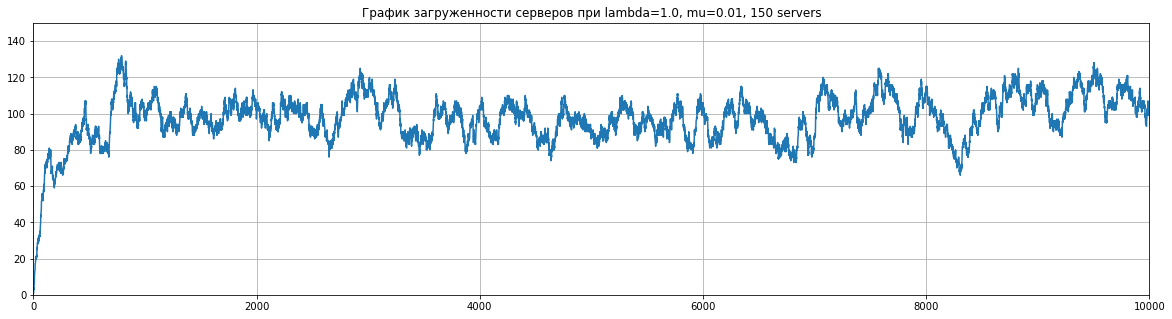
draw_downtime_plot(10, 5)draw_load_plot(1, 10, 20, 300)draw_load_plot(1, 100, 150, 10000)На наш взгляд, отличающей особенностью данной системы является то, что даже при большой нагрузке и долгом времени обработки систему можно сбалансировать при помощи достаточного количества серверов.
Если бы мы решали некую бизнес задачу, то зная сколько примерно будет обрабатываться заявка, и спрогнозировав поток пользователей, можно подготовиться, поставить больше серверов и избежать потери денег от упущенных клиентов.
def Pi_n(lambda_, mu_, n):
return pow(lambda_/mu_, n)/math.factorial(n)def Pi_0(lambda_, mu_, n):
return 1/(sum([Pi_n(lambda_, mu_, i) for i in range(n+1)]))def theoretical_stationary_probabilities(lambda_, mu_, n):
pi0 = Pi_0(lambda_, mu_, n)
return [Pi_n(lambda_, mu_, i)*pi0 for i in range(n+1)]def theoretical_average_load(lambda_, mu_, n):
probs = theoretical_stationary_probabilities(lambda_, mu_, n)
return sum([server_number*probs[server_number] for server_number in range(len(probs))])def theoretical_reject_probability(lambda_, mu_, n):
return pow((lambda_/mu_), n) / math.factorial(n) * Pi_0(lambda_, mu_, n)def theoretical_absolute_bandwith(lambda_, mu_, n):
return lambda_*theoretical_relative_bandwith(lambda_, mu_, n)def theoretical_relative_bandwith(lambda_, mu_, n):
return 1 - theoretical_reject_probability(lambda_, mu_, n)theoretical_stationary_probabilities(1, 1, 5)[0.3680981595092025,
0.3680981595092025,
0.18404907975460125,
0.06134969325153375,
0.015337423312883437,
0.0030674846625766876]
res = simulate(1, 1, 5, 1000)
stationary_probabilities(res, 5)[0.38186385167175807,
0.37123960415530505,
0.17377990775547525,
0.05149536571912897,
0.017145006218107647,
0.0031251705646565104]
res = simulate(1, 1, 5, 10000)
stationary_probabilities(res, 5)[0.3628174160056652,
0.3796408483513869,
0.18326411803912182,
0.058408526082050896,
0.013642145384177597,
0.0021590971551570456]
Видим, что вычисленные вероятности для состояний системы очень близки к теоретическим стационарным вероятностям для фиксированного K
theoretical_stationary_probabilities(1/10, 1/3, 5)[0.7408188010921892,
0.2222456403276568,
0.03333684604914852,
0.0033336846049148534,
0.000250026345368614,
1.5001580722116842e-05]
res = simulate(10, 3, 5, 1000)
stationary_probabilities(res, 5)[0.7537123739225232,
0.2019433859525935,
0.03113149422303651,
0.006245723472419933,
0.0,
0.0]
res = simulate(10, 3, 5, 10000)
stationary_probabilities(res, 5)[0.7272683087900984,
0.23328096861796882,
0.03587112374397565,
0.0032924708189850153,
2.6912830856784126e-05,
0.0]
theoretical_stationary_probabilities(1, 1/2, 5)[0.13761467889908258,
0.27522935779816515,
0.27522935779816515,
0.1834862385321101,
0.09174311926605505,
0.03669724770642202]
res = simulate(1, 2, 5, 1000)
stationary_probabilities(res, 5)[0.1717422492737713,
0.2816295883340158,
0.27667477588701944,
0.17148692123286652,
0.07384071952570047,
0.024509088206684442]
res = simulate(1, 2, 5, 10000)
stationary_probabilities(res, 5)[0.15579040673518188,
0.28068774320734985,
0.2741267454674457,
0.17731608813100588,
0.08831587610189033,
0.02363894756496464]
res = simulate(2, 3, 5, 10000)print(reject_probability(res))
print(theoretical_reject_probability(1/2, 1/3, 5))0.011897435897435898
0.014183155314305725
print(relative_bandwith(res))
print(theoretical_relative_bandwith(1/2, 1/3, 5))0.9881025641025641
0.9858168446856943
print(absolute_bandwith(res))
print(theoretical_absolute_bandwith(1/2, 1/3, 5))0.4815971831182091
0.49290842234284715
print(average_load(res, 1/3))
print(theoretical_average_load(1/2, 1/3, 5))1.4447915493546273
1.4787252670285413
print(downtime_probability(res))
print(Pi_0(1/2, 1/3, 5))0.2287133380814342
0.22412887410260898