AI model that solves an 8-puzzle problem using the A* search algorithm.
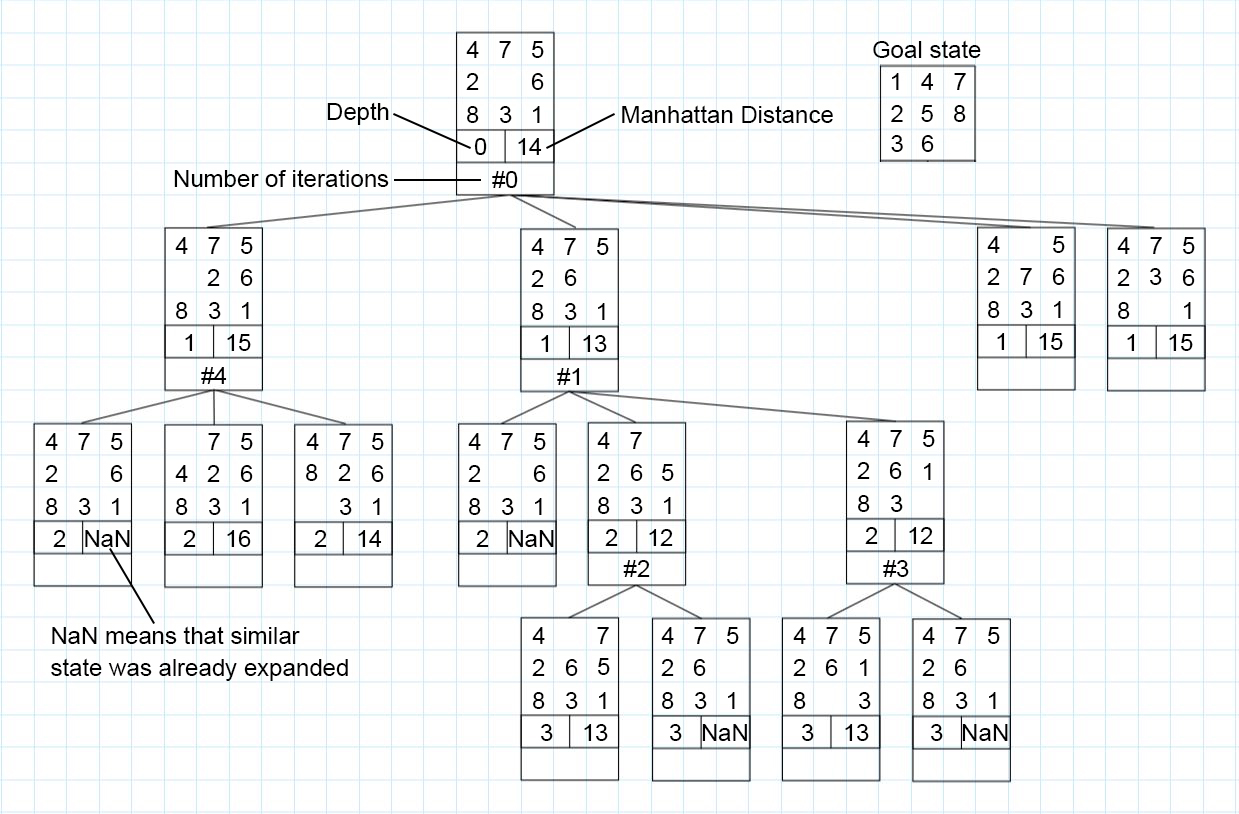
The proposed algorithm was written in MATLAB as a possible solver for the 8-puzzle problem. An 8-puzzle can be imagined as a 3-by-3 grid with 8 blocks located inside this grid (Illustrated in Figure 1). The blocks are numbered 1 through 8 with one empty space. To solve this puzzle one needs to reorder the blocks in a numerical order by moving blocks only with the empty space.
Figure 1. 8-puzzle
The 8-puzzle problem can be solved by the following algorithm (Depicted in Figure 2):
- Accept the initial state and goal state input;
- Check if the empty square can move up, down, left, or right;
- Write down all new matrices obtained after performing the move in each possible direction;
- Write down actual cost to reach the state, g – the depth of all new matrices;
- Calculate heuristic function h – total Manhattan distance or number of misplaced tiles (depending on the initial choice) for each new matrix and write it down;
- Calculate evaluation function f by adding g to h for each new matrix;
- Find all minimum values of f;
- If there are more than one minimum value f algorithm picks the one with the smaller depth g;
- The matrix that corresponds to the minimum value f becomes the current state;
- Algorithm checks if the current state occurs among any known matrices. If it does then their values f are set as NaN and Step 9 is repeated. By doing so one can assure that algorithm will not take the same matrix repeatedly;
- Current state gets expanded;
- Steps 2 – 9 are applied to all the matrices obtained after expanding until the goal state occurs as the current state.
Figure 2. Example of the algorithm