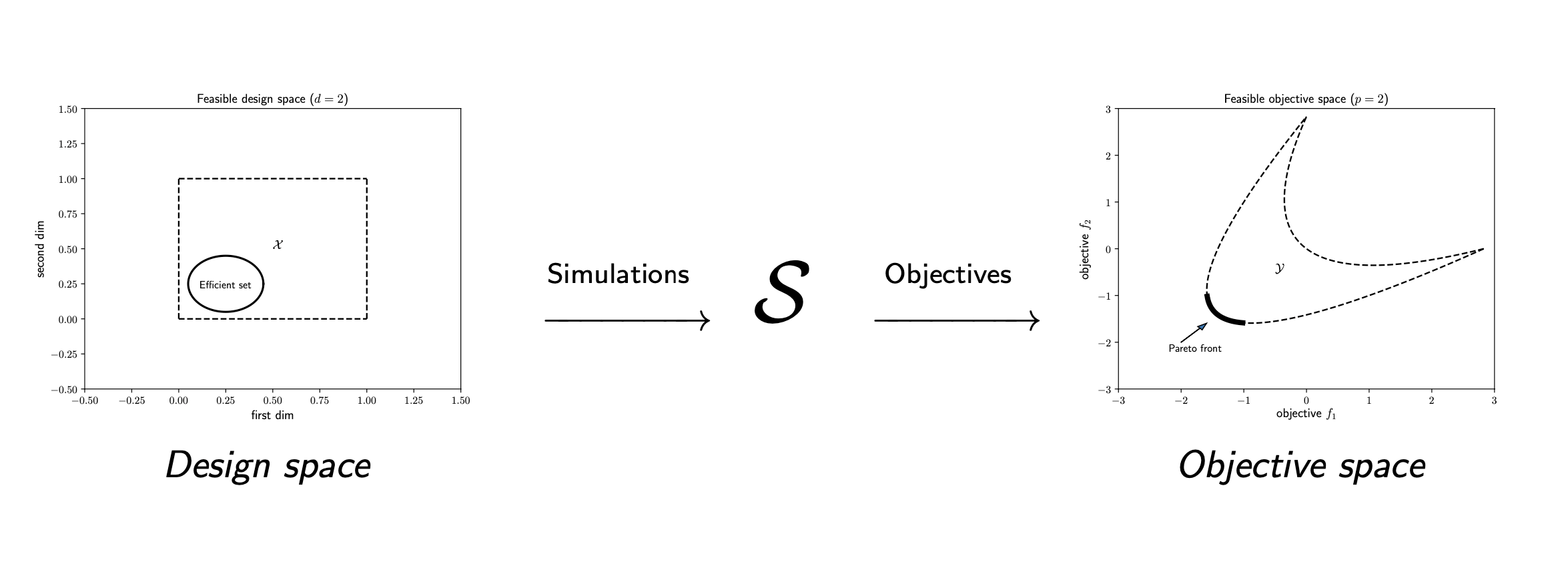
ParMOO is a parallel multiobjective optimization solver that seeks to exploit simulation-based structure in objective and constraint functions.
To exploit structure, ParMOO models simulations separately from objectives and constraints. In our language:
- a design variable is an input to the problem, which we can directly control;
- a simulation is an expensive or time-consuming process, including real-world experimentation, which is treated as a blackbox function of the design variables and evaluated sparingly;
- an objective is an algebraic function of the design variables and/or simulation outputs, which we would like to optimize; and
- a constraint is an algebraic function of the design variables and/or simulation outputs, which cannot exceed a specified bound.
To solve a multiobjective optimization problem (MOOP), we use surrogate models of the simulation outputs, together with the algebraic definition of the objectives and constraints.
ParMOO is implemented in Python. In order to achieve scalable parallelism, we use libEnsemble to distribute batches of simulation evaluations across parallel resources.
ParMOO has been tested on Unix/Linux and MacOS systems.
ParMOO's base has the following dependencies:
Additional dependencies are needed to use the additional features in
parmoo.extras:
- libEnsemble -- for managing parallel simulation evaluations
And for using the Pareto front visualization library in parmoo.viz:
The easiest way to install ParMOO is via the Python package index, PyPI
(commonly called pip):
pip install < --user > parmoowhere the braces around < --user > indicate that the --user flag is
optional.
To install all dependencies (including libEnsemble) use:
pip install < --user > "parmoo[extras]"You can also clone this project from our GitHub and pip install it
in-place, so that you can easily pull the latest version or checkout
the develop branch for pre-release features.
On Debian-based systems with a bash shell, this looks like:
git clone https://github.com/parmoo/parmoo
cd parmoo
pip install -e .Alternatively, the latest release of ParMOO (including all required and
optional dependencies) can be installed from the conda-forge channel using:
conda install --channel=conda-forge parmooBefore doing so, it is recommended to create a new conda environment using:
conda create --name channel-name
conda activate channel-nameIf you have pytest with the pytest-cov plugin and flake8 installed, then you can test your installation.
python3 setup.py testThese tests are run regularly using GitHub Actions.
ParMOO uses numpy in an object-oriented design, based around the MOOP
class. To get started, create a MOOP object.
from parmoo import MOOP
from parmoo.optimizers import LocalGPS
my_moop = MOOP(LocalGPS)To summarize the framework, in each iteration ParMOO models each simulation
using a computationally cheap surrogate, then solves one or more scalarizations
of the objectives, which are specified by acquisition functions.
Read more about this framework at our ReadTheDocs page.
In the above example, LocalGPS is the class of optimizers that the
my_moop will use to solve the scalarized surrogate problems.
Next, add design variables to the problem as follows using the
MOOP.addDesign(*args) method. In this example, we define one continuous
and one categorical design variable.
Other options include integer, custom, and raw (using raw variables is not
recommended except for expert users).
# Add a single continuous design variable in the range [0.0, 1.0]
my_moop.addDesign({'name': "x1", # optional, name
'des_type': "continuous", # optional, type of variable
'lb': 0.0, # required, lower bound
'ub': 1.0, # required, upper bound
'tol': 1.0e-8 # optional tolerance
})
# Add a second categorical design variable with 3 levels
my_moop.addDesign({'name': "x2", # optional, name
'des_type': "categorical", # required, type of variable
'levels': ["good", "bad"] # required, category names
})Next, add simulations to the problem as follows using the
MOOP.addSimulation method. In this example, we define a toy simulation
sim_func(x).
import numpy as np
from parmoo.searches import LatinHypercube
from parmoo.surrogates import GaussRBF
# Define a toy simulation for the problem, whose outputs are quadratic
def sim_func(x):
if x["x2"] == "good":
return np.array([(x["x1"] - 0.2) ** 2, (x["x1"] - 0.8) ** 2])
else:
return np.array([99.9, 99.9])
# Add the simulation to the problem
my_moop.addSimulation({'name': "MySim", # Optional name for this simulation
'm': 2, # This simulation has 2 outputs
'sim_func': sim_func, # Our sample sim from above
'search': LatinHypercube, # Use a LH search
'surrogate': GaussRBF, # Use a Gaussian RBF surrogate
'hyperparams': {}, # Hyperparams passed to internals
'sim_db': { # Optional dict of precomputed points
'search_budget': 10 # Set search budget
},
})Now we can add objectives and constraints using MOOP.addObjective(*args)
and MOOP.addConstraint(*args). In this example, there are 2 objectives
(each corresponding to a single simulation output) and one constraint.
# First objective just returns the first simulation output
my_moop.addObjective({'name': "f1", 'obj_func': lambda x, s: s["MySim"][0]})
# Second objective just returns the second simulation output
my_moop.addObjective({'name': "f2", 'obj_func': lambda x, s: s["MySim"][1]})
# Add a single constraint, that x[0] >= 0.1
my_moop.addConstraint({'name': "c1",
'constraint': lambda x, s: 0.1 - x["x1"]})Finally, we must add one or more acquisition functions using
MOOP.addAcquisition(*args). These are used to scalarize the surrogate
problems. The number of acquisition functions typically determines the
number of simulation evaluations per batch. This is useful to know if you
are using a parallel solver.
from parmoo.acquisitions import UniformWeights
# Add 3 acquisition functions
for i in range(3):
my_moop.addAcquisition({'acquisition': UniformWeights,
'hyperparams': {}})Finally, the MOOP is solved using the MOOP.solve(budget) method, and the
results can be viewed using MOOP.getPF() method.
my_moop.solve(5) # Solve with 5 iterations of ParMOO algorithm
results = my_moop.getPF() # Extract the resultsAfter executing the above block of code, the results variable points to
a numpy structured array, each of whose entries corresponds to a
nondominated objective value in the my_moop object's final database.
You can reference individual fields in the results array by using the
name keys that were assigned during my_moop's construction, or
plot the results by using the viz library.
Congratulations, you now know enough to get started solving MOOPs with ParMOO!
Next steps:
- Learn more about all that ParMOO has to offer (including saving and checkpointing, INFO-level logging, advanced problem definitions, and different surrogate and solver options) at our ReadTheDocs page.
- Explore the advanced examples (including a
libEnsembleexample) in theexamplesdirectory.- Install libEnsemble and get started solving MOOPs in parallel.
- To interactively explore your solutions, install its extra dependencies and use our built-in viz tool.
To seek support or report issues, e-mail:
parmoo@mcs.anl.gov
Our full documentation is hosted on:
Please read our LICENSE and CONTRIBUTING files.
Please use one of the following to cite ParMOO.
Our JOSS paper:
@article{parmoo,
author={Chang, Tyler H. and Wild, Stefan M.},
title={{ParMOO}: A {P}ython library for parallel multiobjective simulation optimization},
journal = {Journal of Open Source Software},
volume = {8},
number = {82},
pages = {4468},
year = {2023},
doi = {10.21105/joss.04468}
}Our online documentation:
@techreport{parmoo-docs,
title = {{ParMOO}: {P}ython library for parallel multiobjective simulation optimization},
author = {Chang, Tyler H. and Wild, Stefan M. and Dickinson, Hyrum},
institution = {Argonne National Laboratory},
number = {Version 0.2.2},
year = {2023},
url = {https://parmoo.readthedocs.io/en/latest}
}