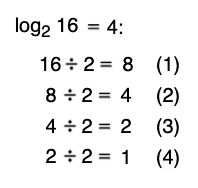- Become familiar with three types of tree data structures: Tree, Binary Tree and Binary Search Tree.
- Identify common use cases for Trees.
- Identify common methods for Trees.
- Consider some of the efficiency issues of using Trees.
- Sequence: a data structure in which data is stored and accessed in a specific order.
- Stack is a linear data structure that follows the principle of Last In First Out (LIFO)
- Index: the location, represented by an integer, of an element in a sequence.
- Iterable: able to be broken down into smaller parts of equal size that can be processed in turn. You can loop through any iterable object.
- Slice: a group of neighboring elements in a sequence.
- List: a mutable data type in Python that can store many types of data. The most common data structure in Python.
- Tuple: an immutable data type in Python that can store many types of data.
- Range: a data type in Python that stores integers in a fixed pattern.
- String: an immutable data type in Python that stores unicode characters in a fixed pattern. Iterable and indexed, just like other sequences.
The next data structure we'll be learning about is the tree. A tree has some similarities to a linked list: both consist of nodes, each of which has a value and a reference to other nodes. Unlike a linked list, however, which only points to a single "next" node, nodes in trees can point to multiple child nodes. For this reason, a tree can be used to represent more complex data relationships than can be expressed using a linked list or other linear data structure.
In the context of computing and data structures (as in the real world), there are lots of different types of trees. In this lesson, we'll first learn about the most general type of tree, and then look at a couple of special cases that place certain constraints on how the tree is structured.
A tree is a data structure that consists of a node (called the root node) that can have zero or more child nodes. Each child node can, in turn, have zero or more children of its own:
When we represent a tree in code, each of its nodes will have two attributes: a value or data of some sort and an list containing a list of references to its child nodes. Although the diagrams in this lesson show nodes with values that are integers, the value of a node can be of any data type.
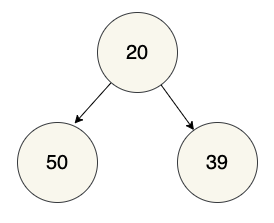
Say we have the following very simple tree that we need to represent in code:
Each node in our tree would be a hash containing key/value pairs for the two attributes:
child_one = {
'value': 50,
'children': []
}
child_two = {
'value': 39,
'children': []
}
root_node = {
'value': 20,
'children': [
child_one,
child_two
]
}Each element in a node's children list is itself a node:
root_node
# => { value: 20, children: [ { value: 45, children: [] }, ... ] }
root_node.get('children')[0]
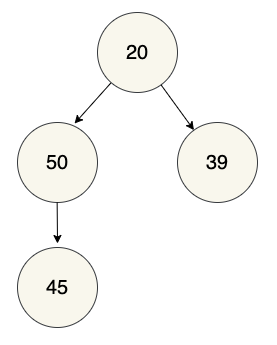
# => { value: 50, children: [] }If we were to add a child node to child_one, with a value of 45:
The updated code would look like this:
child_three = {
'value': 45,
'children': []
}
child_one = {
'value': 50,
'children': [child_three]
}
child_two = {
'value': 39,
'children': []
}
root_node = {
'value': 20,
'children': [
child_one,
child_two
]
}A binary tree is a special kind of tree in which each node has at most two child nodes, referred to as the left child and right child.
Each node in a binary tree has three attributes: a value, and references to
its left_child and right_child. If a node doesn't have either or both of
these child nodes, the attributes will be set to nil.
We can revisit the simple example we used above because that tree also meets the definition of a binary tree:
To represent that same structure as a binary tree, the code would look like this:
child_three = {
'value': 45,
'left_child': None,
'right_child': None
}
child_one = {
'value': 50,
'left_child': child_three,
'right_child': None
}
child_two = {
'value': 39,
'left_child': None,
'right_child': None
}
root_node = {
'value': 20,
'left_child': child_one,
'right_child': child_two
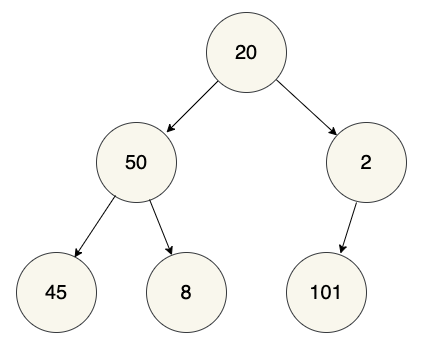
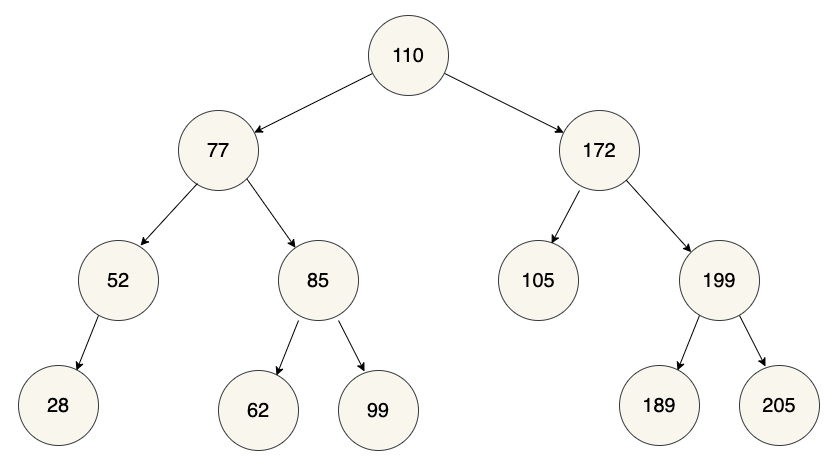
}A binary search tree (BST) is a special kind of a binary tree in which the value of a node's left child (if it has one) must be less than the value of the node itself, and the value of its right child (if it has one) must be greater than the value of the node itself:
If you look at the nodes in the diagram above, you will see that they all meet the constraints: each left child's value is less its parent's value, and each right child's value is greater than its parent's value. However, while this is necessary to make the tree a valid binary search tree, it is not sufficient. We must also verify that all the "left descendants" of a node are less than the parent node. You can see this in the highlighted portion of this diagram:
Notice that all the values in the left half of the diagram are less than 50, the value of the root node. And, if you take a look at the right half of the diagram, you'll see that all those values are greater than 50.
But we still aren't done — we need to do the same check for all the subtrees.
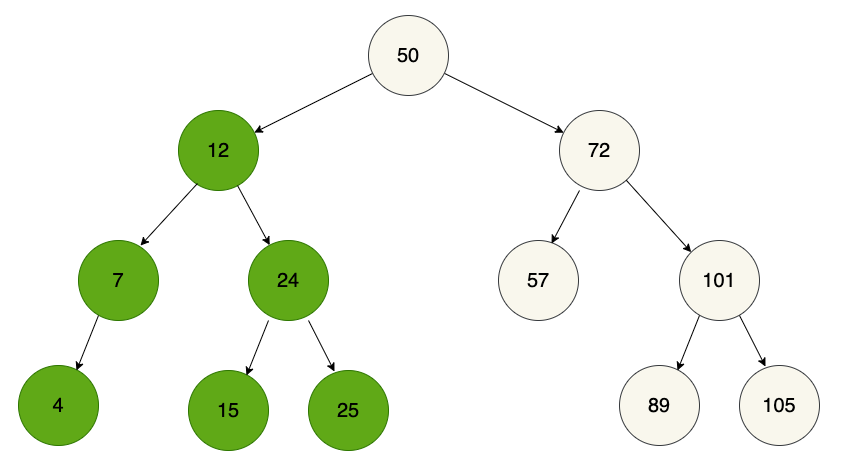
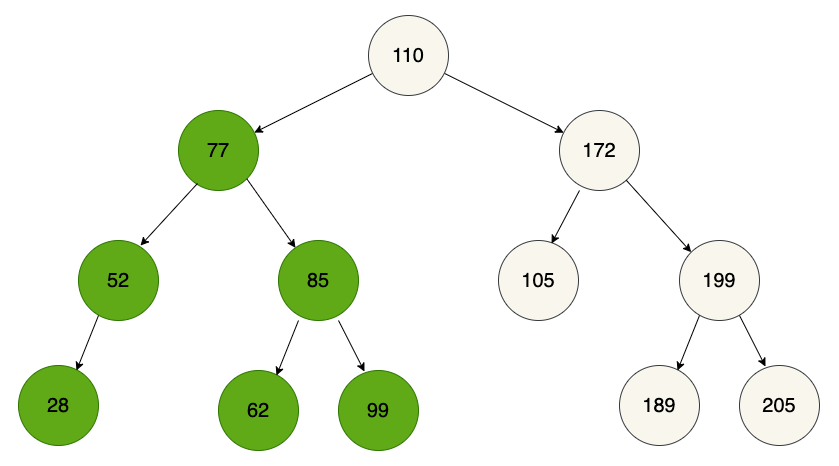
Let's take a look at another example:
First, we'll look at each individual node and its children — so far so good. Each left child is less than its parent and each right child is greater than its parent. So now let's look at the left side overall:
Still good: all the values in the left half of the tree are less than the root node's value. But now, what if we repeat the process for the subtree with the root node that has a value of 77:
The values of both "left descendants" are less than 77, but not all the "right descendants" are greater than 77. If you take another look at the full tree, you'll see a similar issue on the right side:
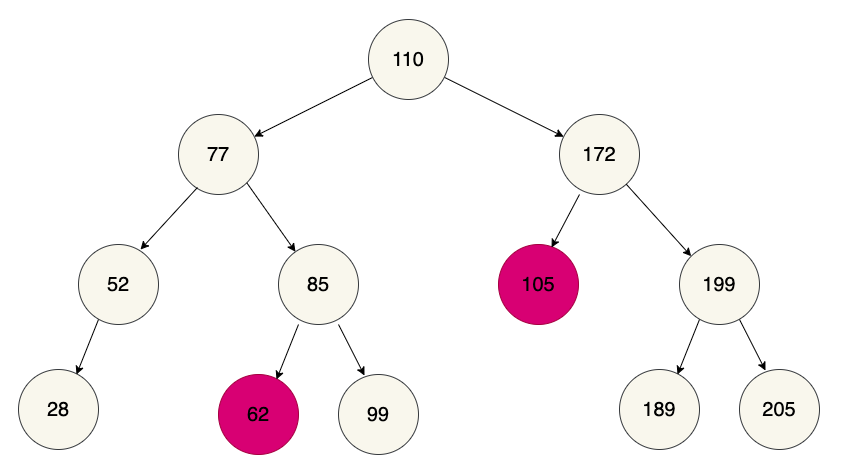
So what benefit is there to constructing a tree with these rigid constraints? If you think about it from the point of view of searching, it makes sense. Say we were searching the tree for the value 62. We would start at the root and compare its value to 62. 62 is less than 110, so we would then proceed to the left child and repeat the comparison. 62 is less than 77 so we would continue down the left side and compare 62 to 52. 62 is greater than 52, but the 52 node doesn't have a right child so we would conclude (incorrectly) that the value we want isn't in the tree.
This is, in fact, the whole point of binary search trees. Let's take another look at our earlier, valid, example:
Say we wanted to search this tree for the value 25. The process would take four steps:
50 -> 12 -> 24 -> 25
If you think through the process for another value or two, you should be able to convince yourself that, with a tree of this height (or number of levels), four is the maximum number of steps it would take to either find the value or determine that it isn't present.
If, on the other hand, we were searching an unordered tree, our only option would be to systematically traverse every node in the tree in turn until we either found the value or finished searching the entire tree (we'll talk about tree traversal in the next lesson). For this example, in the worst case, it would take 12 steps (the number of nodes in our example tree).
Trees give us a way to represent multidimensional data. Unlike a linear structure like an list or linked list, trees can be used to model more complex relationships among elements. Some examples of real-world uses of trees include:
- The DOM
- Computer File Systems, which are organized by folders and subfolders
- Decision trees, sometimes used in Artificial intelligence
The implementation of a Tree class is very similar to what we did for the
LinkedList. It includes two classes: one for the tree itself and one for the
nodes. The Tree class will have a single attribute, root, and, for a
non-binary tree, the Node class will have two attributes: a value and a
children list:
class Tree:
def __init__(self):
self.root = None
class Node:
def initialize(self, value)
self.value = value
self.children = []The implementation for a BinaryTree or BinarySearchTree class would be
almost the same, except rather than a children list, the Node class would
include left_child and right_child attributes:
class BinaryTree: # or BinarySearchTree
def __init__(self):
self.root = None
class Node:
def __init__(self, value)
self.value = value
self.left_child = None
self.right_child = NoneThe methods included in an implementation of a tree structure — and how they are implemented — will vary depending on the type of tree being used and what it's being used for. However, at a minimum, a typical implementation will likely include methods for inserting and removing nodes, and for searching or traversing the tree.
As an example, let's consider an add method to add a new node. If we are using
a simple tree to represent something like a file structure, our goal would
presumably be to add a new child to a particular node, so we would need a way to
reference or find that node and add the new node to its children list. In
this case, it may make sense to create the add method in the Node class. The
method would be called on the node we want to append the new node to, and the
new node would be passed in to the method as an argument. (Alternatively, just
the value could be passed in and the new node created inside the method.)
If, on the other hand, we're adding a new element to a binary search tree, we
would need to define a very specific algorithm to traverse the tree and insert
the new node at the correct location. In this case, the add method would need
to be in the BinarySearchTree class.
Since the methods in a tree implementation will vary depending on what type of tree it is and how it's being used, the Big O of those methods will vary as well.
Using the add example from above, the efficiency in the first case — where
we're adding a new node to a particular parent node — would be O(1).
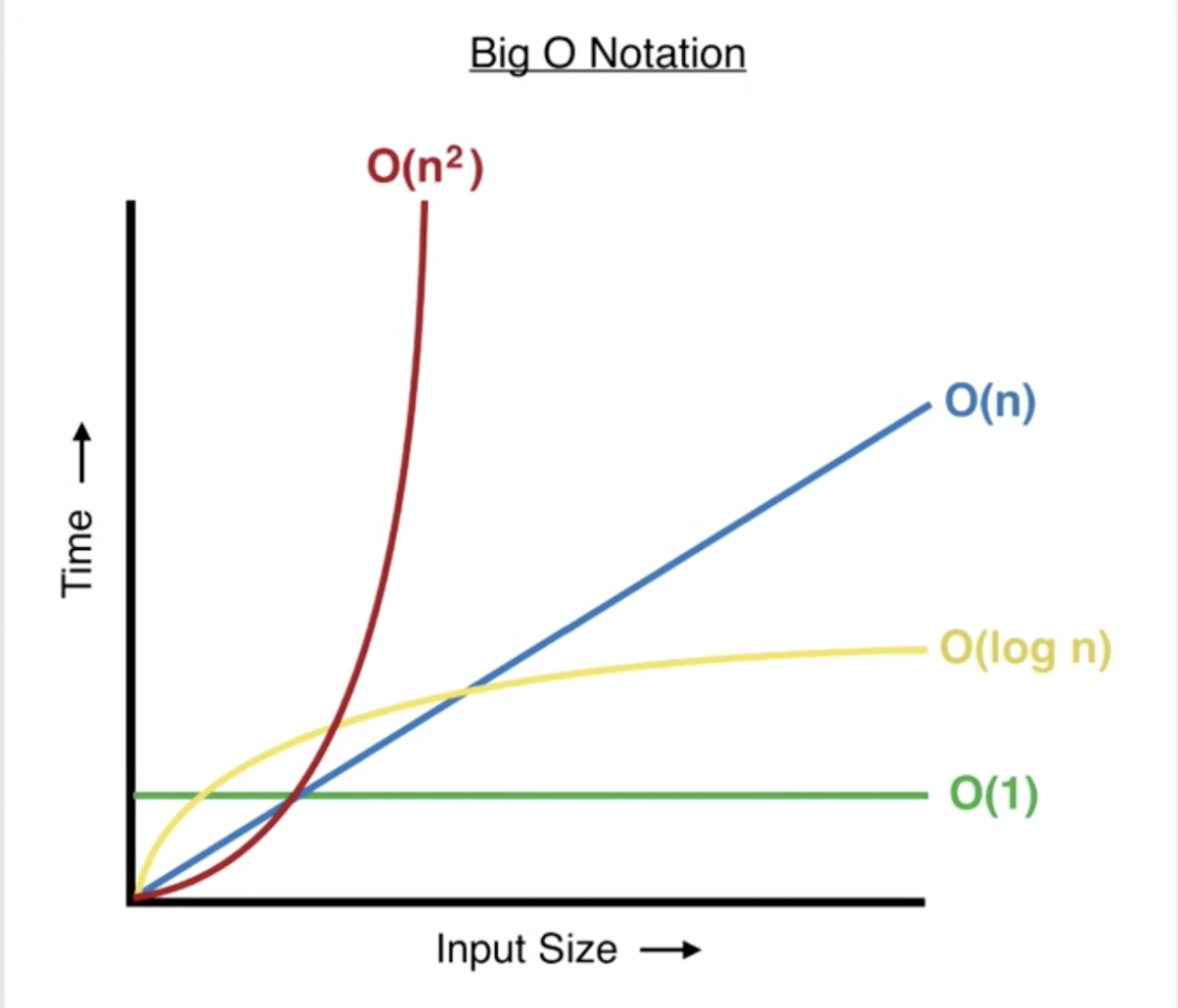
In the second case where we're adding an element into a binary search tree, we will need to do some traversal. However, as we discussed above, the maximum number of steps this took was less than the number of nodes contained in the tree. As it turns out, for search algorithms where you're able to cut the problem in half at each step, the number of steps is approximately equal to log₂n. In Big O notation, this is expressed as O(log n).
If you take a look at how O(log n) looks compared to other common runtimes, we can see that it's great! Not quite as good as constant time, but much better than linear O(n) or quadratic O(n²) time:
Mathematical aside: don't worry too much about the math here. Basically, the log base 2 of a number is the number of times you can divide that number by 2 until you get to 1 or less. For example, log₂16 = 4:
This process of repeatedly dividing by 2 may remind you of how we described the binary search process — that's where the name came from!
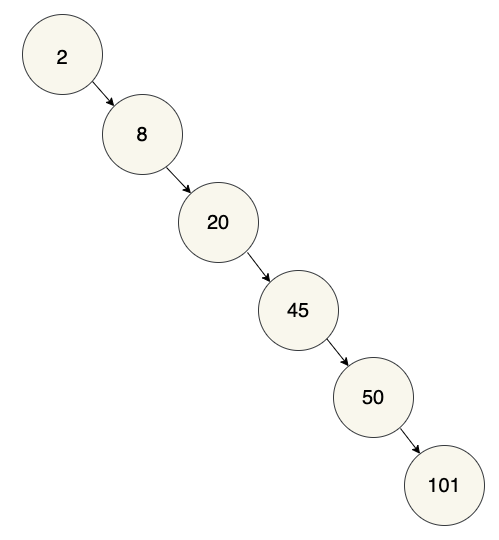
However, there is a big caveat here — the O(log n) is not guaranteed. Let's take a look at an example:
This is a valid binary search tree! All of the right_child nodes have
values greater than the value of their parent; there is no requirement that
nodes have both a right_child and a left_child. But if you think about
searching this binary search tree for the value 101, you should see that it
would take n steps, not log n. (Not surprising given that, for all practical
purposes, this binary search tree is really a linked list!) In order to get the
full benefit of using a binary search tree, it needs to be balanced.
A tree is considered to be balanced if its right subtree and left subtree have the same height (number of levels), or they only differ by 1. The more a binary search tree departs from being balanced (with the example above being the most extreme case), the less efficient it will be. The benefits of using a binary search tree, therefore, need to be balanced against the maintenance costs: regularly checking whether the binary search tree is balanced and re-balancing when it isn't.
Whew! We've covered a lot of information in this lesson about what trees are, how they are constructed, and how they can be used. In the next lesson, we'll learn about different methods of tree traversal.