SHIR

Overview

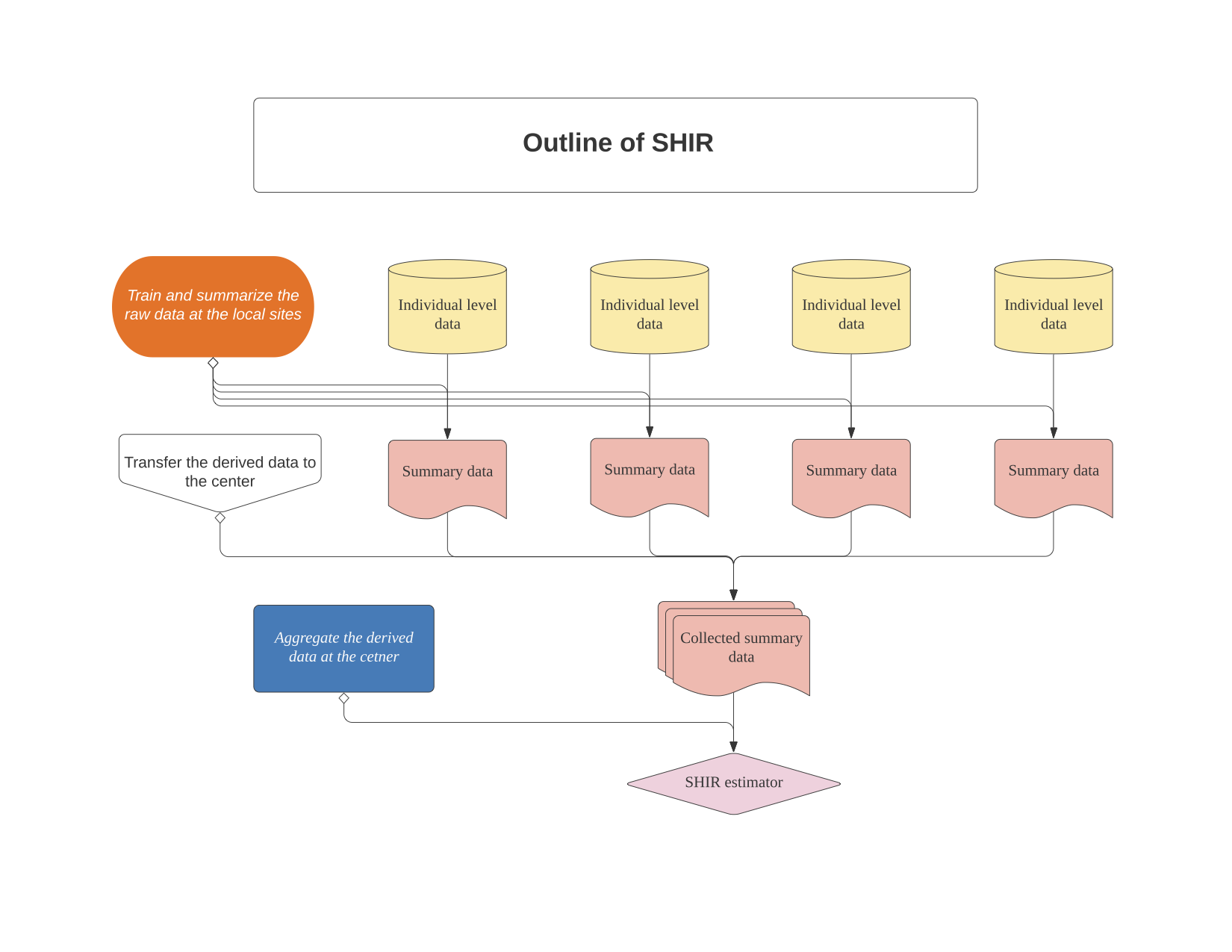
The algorithm performs SHIR, a novel federated learning approach used for aggregating high dimensional and heterogeneous data from local sites, in order to obtain efficient estimators of the logistic model. SHIR protects individual data through a summary-statistics-based integrating procedure. At each local site, it fits LASSO to derive summary data that is free of the individual level information. Susequently, at the central node, it aggregates the derived statistics at the local sites, and produces the integrative estimator.

Background

Meta-analyzing multiple studies allows for more precise estimates and enables investigation of generalizability. However, in the presence of heterogeneity across studies and high dimensional predictors, such integrative analysis is highly challenging. An major application of such integrative analysis is to develop generalizable predictive models using electronic health records (EHR) data from different hospitals. EHR data is subject to high dimensional features and important privacy constraints. The procedure SHIR protects individual data through summary-statistics-based integrating procedure, accommodates between study heterogeneity in both the covariate distribution and model parameters, and attains consistent variable selection.

Flowchart

Key steps

To derive the local individual data

At each local site m with indivdual level data (the response vector and design matrix):

$D^{\sf \scriptscriptstyle (m)}=(Y^{\sf \scriptscriptstyle (m)},X^{\sf \scriptscriptstyle (m)}),$

we fit lasso:

$\widehat\beta_{\sf \scriptscriptstyle LASSO}^{\sf \scriptscriptstyle (m)}={\rm argmin}_{\beta}\widehat L(Y^{\sf \scriptscriptstyle (m)};X^{\sf \scriptscriptstyle (m)}\beta)+\lambda_m\|\beta_{-1}\|_1,$

to obtain the summary data (the sample size, hessian matrix, and gradient):

$\{n_m,\widehat H_m,\widehat g_m\},\quad\mbox{where}\quad\widehat H_m=\nabla^2\widehat L_m(\widehat\beta_{\sf \scriptscriptstyle LASSO}^{\sf \scriptscriptstyle (m)});\quad\widehat g_m=\widehat H_m\widehat\beta_{\sf \scriptscriptstyle LASSO}^{\sf \scriptscriptstyle (m)}-\nabla\widehat L_m(\widehat\beta_{\sf \scriptscriptstyle LASSO}^{\sf \scriptscriptstyle (m)}),$

and transfer them to the center node for integrative analysis.

To aggregate the summary data

At the center node, we decompose the coefficients into mean effects and heterogeneous effects:

$\{\mu,\alpha^{(\bullet)}\}~\mbox{where}~\alpha^{(\bullet)}=(\alpha^{\sf \scriptscriptstyle (1)},...,\alpha^{\sf \scriptscriptstyle (M)}),~\beta^{\sf \scriptscriptstyle (m)}=\mu+\alpha^{\sf \scriptscriptstyle (m)},~\alpha^{\sf \scriptscriptstyle (1)}+\cdots+\alpha^{\sf \scriptscriptstyle (M)}=0,$

and fit the quadratic-approximated integrative regression:

$\{\widehat\mu_{\sf \scriptscriptstyle SHIR},\widehat\alpha^{(\bullet)}_{\sf \scriptscriptstyle SHIR}\}={\rm argmin}_{\mu,\alpha^{(\bullet)}}N^{-1} \sum_{m=1}^M n_mQ_m(\mu,\alpha^{\sf \scriptscriptstyle (m)})+\lambda(\|\mu_{-1}\|_1+\lambda_g\|\alpha^{(\bullet)}_{-1}\|_{2,1}),$

$\mbox{where}\quad Q_m(\mu,\alpha^{\sf \scriptscriptstyle (m)})=(\mu+\alpha^{\sf \scriptscriptstyle (m)})^{\sf \scriptscriptstyle T}\widehat H_m(\mu+\alpha^{\sf \scriptscriptstyle (m)}) -2\widehat g_m^{\sf \scriptscriptstyle T}(\mu+\alpha^{\sf \scriptscriptstyle (m)}),$

to obtain the SHIR estimator. Please see more details from the SHIR paper linked in the citation section.

Installation

The development version of this package can be installed from GitHub with:

# install.packages("devtools")
devtools::install_github("celehs/SHIR")

Getting started

Follow the main steps displayed in the example, in which we apply SHIR to a simulated dataset.

Citation

Cai, T., Liu, M., & Xia, Y. (2021). Individual data protected integrative regression analysis of high-dimensional heterogeneous data. Journal of the American Statistical Association, (just-accepted), 1-34. https://www.tandfonline.com/doi/abs/10.1080/01621459.2021.1904958

celehs / SHIR