Kotlin∇ is a type-safe automatic differentiation framework written in Kotlin. It allows users to express differentiable programs with higher-dimensional data structures and operators. We attempt to restrict syntactically valid constructions to those which are algebraically valid and can be checked at compile-time. By enforcing these constraints in the type system, it eliminates certain classes of runtime errors that may occur during the execution of a differentiable program. Due to type-inference, most type declarations may be safely omitted by the end-user. Kotlin∇ strives to be expressive, safe, and notationally similar to mathematics.
- Introduction
- Supported features
- Usage
- Visualization
- Testing and gradient checking
- How does it work?
- Experimental ideas
- Formal grammar
- UML diagram
- Comparison to other frameworks
- References
- Acknowledgements
Inspired by Stalin∇, Autograd, DiffSharp, Myia, Nexus, Tangent, Lantern et al., Kotlin∇ attempts to port recent advancements in automatic differentiation (AD) to the Kotlin language. AD is useful for gradient descent and has a variety of applications in numerical optimization and machine learning. Our implementation adds a number of experimental ideas, including compile-time shape-safety, algebraic simplification and numerical stability checking with property-based testing. We aim to provide an algebraically-grounded implementation of AD for shape-safe tensor operations. Tensors in Kotlin∇ are represented as multidimensional arrays.
Kotlin∇ currently supports the following features:
- Arithmetical operations on scalars, vectors and matrices
- Shape-safe vector and matrix algebra
- Partial and higher-order differentiation on scalars
- Property-based testing for numerical gradient checking
- Recovery of symbolic derivatives from AD
Additionally, it aims to support:
- PyTorch-style define-by-run semantics
- N-dimensional tensors and higher-order tensor operators
- Fully-general AD over control flow, variable reassignment (via delegation), and array programming, possibly using a typed IR such as Myia
All of these features are implemented without access to bytecode or special compiler tricks - just using higher-order functions and lambdas as shown in Lambda the Ultimate Backpropogator, embedded DSLs a la Lightweight Modular Staging, and ordinary generics. Please see below for a more detailed feature comparison.
Kotlin∇ is hosted on Maven Central. An example project is provided here.
dependencies {
implementation("ai.hypergraph:kotlingrad:0.4.7")
}<dependency>
<groupId>ai.hypergraph</groupId>
<artifactId>kotlingrad</artifactId>
<version>0.4.7</version>
</dependency>To access Kotlin∇'s notebook support, use the following line magic:
@file:DependsOn("ai.hypergraph:kotlingrad:0.4.7")For more information, explore the tutorial.
Kotlin∇ operators are higher-order functions, which take at most two inputs and return a single output, all of which are functions with the same numerical type, and whose shape is denoted using superscript in the rightmost column below.
| Math | Infix † | Prefix | Postfix‡ | Operator Type Signature |
|---|---|---|---|---|
|
|
a(b)a of b
|
|||
a + ba - b
|
plus(a, b)minus(a, b)
|
|||
a * ba.times(b)
|
times(a, b) |
|||
|
|
a / ba.div(b)
|
div(a, b) |
||
-a+a
|
a.neg()a.pos()
|
|||
|
|
sin(a)cos(a)tan(a)
|
a.sin()a.cos()a.tan()
|
||
ln(a)log(a)
|
a.ln()a.log()
|
|||
a.log(b) |
log(a, b) |
|||
a.pow(b) |
pow(a, b) |
|||
|
|
a.pow(1.0/2)a.root(3)
|
sqrt(a)cbrt(a)
|
a.sqrt()a.cbrt()
|
|
|
|
a.d(b)d(a) / d(b)
|
grad(a)[b] |
||
grad(a) |
a.grad() |
|||
a.d(b)a.grad(b)
|
grad(a, b)grad(a)[b]
|
|||
divg(a) |
a.divg() |
|||
curl(a) |
a.curl() |
|||
grad(a) |
a.grad() |
|||
hess(a) |
a.hess() |
|||
lapl(a) |
a.lapl() |
ℝ can be a Double, Float or BigDecimal. Specialized operators are defined for subsets of ℝ, e.g., Int, Short or BigInteger for subsets of ℤ, however differentiation is only defined for continuously differentiable functions on ℝ.
† a and b are higher-order functions. These may be constants (e.g., 0, 1.0), variables (e.g., Var()) or expressions (e.g., x + 1, 2 * x + y).
‡ For infix notation, . is optional. Parentheses are also optional depending on precedence.
§ Matrix division is defined iff B is invertible, although it could be possible to redefine this operator using the Moore-Penrose inverse.
∗ Where C(ℝm) is the space of all continuous functions over ℝ. If the function is not over ℝ, it will fail at compile-time. If the function is over ℝ but not continuous differentiable at the point under consideration, it will fail at runtime.
? The input shape is tracked at runtime, but not at the type level. While it would be nice to infer a union type bound over the inputs of binary functions, it is likely impossible using the Kotlin type system without great effort. If the user desires type checking when invoking higher order functions with literal values, they will need to specify the combined input type explicitly or do so at runtime.
τ, λ, π, ω Arbitrary products.
Kotlin∇ supports derivatives between tensors of up to rank 2. The shape of a tensor derivative depends on (1) the shape of the function under differentiation and (2) the shape of the variable with respect to which we are differentiating.
| I/O Shape | |||
|---|---|---|---|
| ❌ | |||
| ❌ | ❌ |
Matrix-by-vector, vector-by-matrix, and matrix-by-matrix derivatives require rank 3+ tensors and are currently unsupported.
Kotlin∇ supports arbitrary order derivatives on scalar functions, and up to 2nd order derivatives on vector functions. Higher-order derivatives on matrix functions are unsupported.
Shape safety is an important concept in Kotlin∇. There are three broad strategies for handling shape errors:
- Hide the error somehow by implicitly reshaping or broadcasting arrays
- Announce the error at runtime, with a relevant message, e.g.,
InvalidArgumentError - Do not allow programs which can result in a shape error to compile
In Kotlin∇, we use the last strategy to check the shape of tensor operations. Consider the following program:
// Inferred type: Vec<Double, D2>
val a = Vec(1.0, 2.0)
// Inferred type: Vec<Double, D3>
val b = Vec(1.0, 2.0, 3.0)
val c = b + b
// Does not compile, shape mismatch
// a + bAttempting to sum two vectors whose shapes do not match will fail to compile, and they must be explicitly resized.
// Inferred type: Mat<Double, D1, D4>
val a = Mat1x4(1.0, 2.0, 3.0, 4.0)
// Inferred type: Mat<Double, D4, D1>
val b = Mat4x1(1.0, 2.0, 3.0, 4.0)
val c = a * b
// Does not compile, inner dimension mismatch
// a * a
// b * bSimilarly, attempting to multiply two matrices whose inner dimensions do not match will fail to compile.
val a = Mat2x4(
1.0, 2.0, 3.0, 4.0,
5.0, 6.0, 7.0, 8.0
)
val b = Mat4x2(
1.0, 2.0,
3.0, 4.0,
5.0, 6.0,
7.0, 8.0
)
// Types are optional, but encouraged
val c: Mat<Double, D2, D2> = a * b
val d = Mat2x1(1.0, 2.0)
val e = c * d
val f = Mat3x1(1.0, 2.0, 3.0)
// Does not compile, inner dimension mismatch
// e * fExplicit types are optional but encouraged. Type inference helps preserve shape information over long programs.
fun someMatFun(m: Mat<Double, D3, D1>): Mat<Double, D3, D3> = ...
fun someMatFun(m: Mat<Double, D2, D2>) = ...When writing a function, it is mandatory to declare the input type(s), but the return type may be omitted. Shape-safety is currently supported up to rank-2 tensors, i.e. matrices.
The following example shows how to derive higher-order partials of a function z of type ℝ²→ℝ:
val z = x * (-sin(x * y) + y) * 4 // Infix notation
val `∂z∕∂x` = d(z) / d(x) // Leibniz notation [Christianson, 2012]
val `∂z∕∂y` = d(z) / d(y) // Partial derivatives
val `∂²z∕∂x²` = d(`∂z∕∂x`) / d(x) // Higher-order derivatives
val `∂²z∕∂x∂y` = d(`∂z∕∂x`) / d(y) // Higher-order partials
val `∇z` = z.grad() // Gradient operator
val values = arrayOf(x to 0, y to 1)
println("z(x, y) \t= $z\n" +
"z(${values.map { it.second }.joinToString()}) \t\t= ${z(*values)}\n" +
"∂z/∂x \t\t= $`∂z∕∂x` \n\t\t= " + `∂z∕∂x`(*values) + "\n" +
"∂z/∂y \t\t= $`∂z∕∂y` \n\t\t= " + `∂z∕∂y`(*values) + "\n" +
"∂²z/∂x² \t= $`∂z∕∂y` \n\t\t= " + `∂²z∕∂x²`(*values) + "\n" +
"∂²z/∂x∂y \t= $`∂²z∕∂x∂y` \n\t\t= " + `∂²z∕∂x∂y`(*values) + "\n" +
"∇z \t\t= $`∇z` \n\t\t= [${`∇z`[x]!!(*values)}, ${`∇z`[y]!!(*values)}]ᵀ")Any backticks and unicode characters above are simply for readability and have no effect on the behavior. Running this program via ./gradlew HelloKotlingrad should produce the following output:
z(x, y) = ((x) * ((- (sin((x) * (y)))) + (y))) * (4.0)
z(0, 1) = 0.0
∂z/∂x = d(((x) * ((- (sin((x) * (y)))) + (y))) * (4.0)) / d(x)
= 4.0
∂z/∂y = d(((x) * ((- (sin((x) * (y)))) + (y))) * (4.0)) / d(y)
= 0.0
∂²z/∂x² = d(((x) * ((- (sin((x) * (y)))) + (y))) * (4.0)) / d(y)
= 4.0
∂²z/∂x∂y = d(d(((x) * ((- (sin((x) * (y)))) + (y))) * (4.0)) / d(x)) / d(y)
= 4.0
∇z = {y=d(((x) * ((- (sin((x) * (y)))) + (y))) * (4.0)) / d(y), x=d(((x) * ((- (sin((x) * (y)))) + (y))) * (4.0)) / d(x)}
= [4.0, 0.0]ᵀ
Not only does Kotlin∇'s type system encode output shape, it is also capable of tracking free and bound variables, for order-independent name binding and partial application. Expressions inhabited by free variables are typed as functions until fully bound, at which time they return a concrete value. Consider the following example:
val q = X + Y * Z + Y + 0.0
val p0 = q(X to 1.0, Y to 2.0, Z to 3.0) // Name binding
val p1 = q(X to 1.0, Y to 1.0)(Z to 1.0) // Variadic currying
val p3 = q(Z to 1.0)(X to 1.0, Y to 1.0) // Any order is possible
val p4 = q(Z to 1.0)(X to 1.0)(Y to 1.0) // Proper currying
val p5 = q(Z to 1.0)(X to 1.0) // Returns a partially applied function
val p6 = (X + Z + 0)(Y to 1.0) // Does not compileThis feature is made possible by encoding a type-level Hasse diagram over a small set of predefined variable names, with skip-connections for variadic combination and partial application. Curious readers may glean further details by referring to the implementation and usage example.
Kotlin∇ provides various graphical tools that can be used for visual debugging.
Kotlin∇ functions are a type of directed acyclic graph, called dataflow graphs (DFGs). For example, running the expression ((1 + x * 2 - 3 + y + z / y).d(y).d(x) + z / y * 3 - 2).render() will display the following DFG:
Red and blue edges indicate the right and left inputs to a binary operator, respectively. Consider the DFG for a batch of stochastic gradients on linear regression, which can be written in matrix form as :
Thetas represent the hidden parameters under differentiation and the constants are the batch inputs (X) and targets (Y). When all the free variables are bound to numerical values, the graph collapses into a single node, which can be unwrapped into a Kotlin Number.
To generate the sample 2D plots below, run ./gradlew Plot2D.
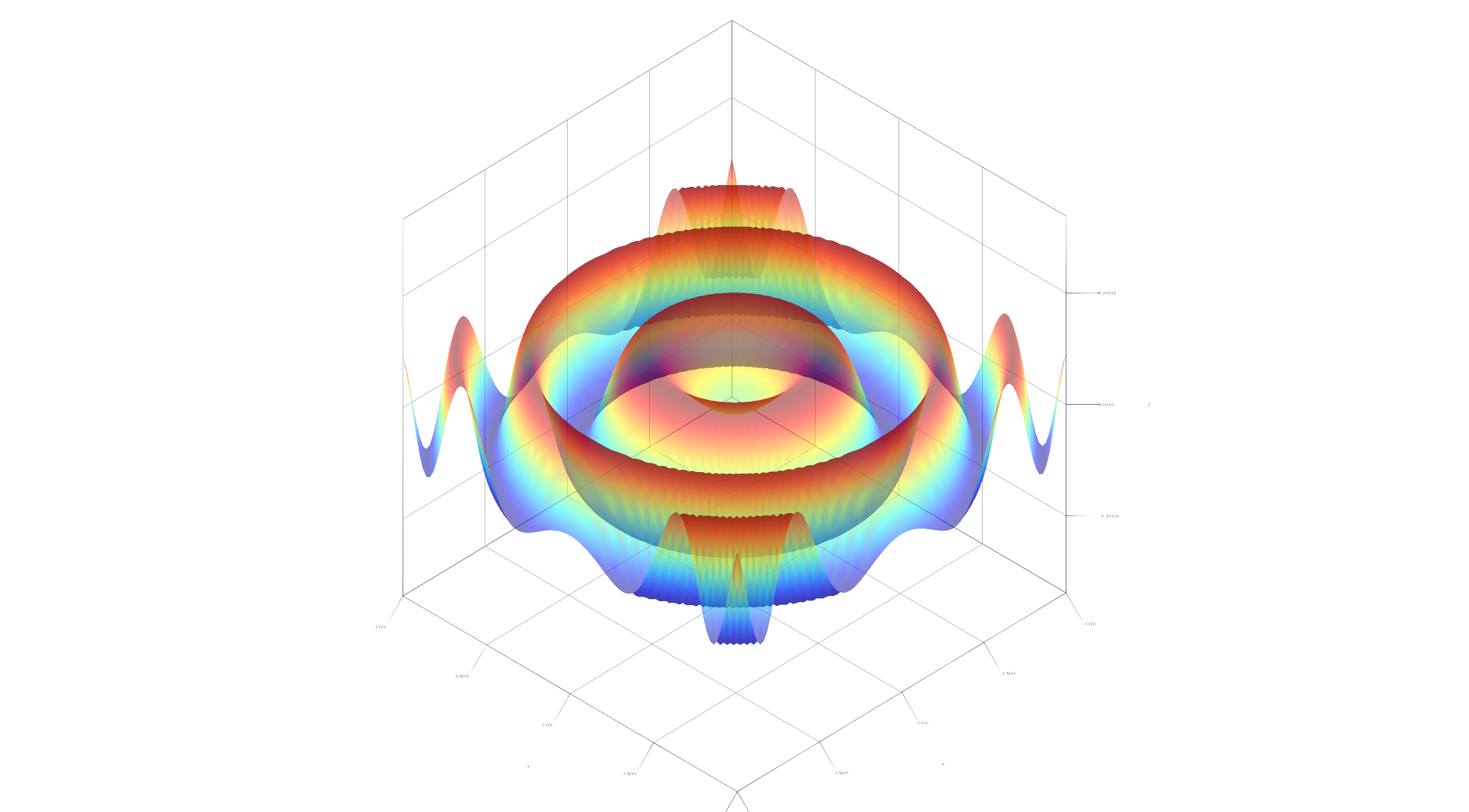
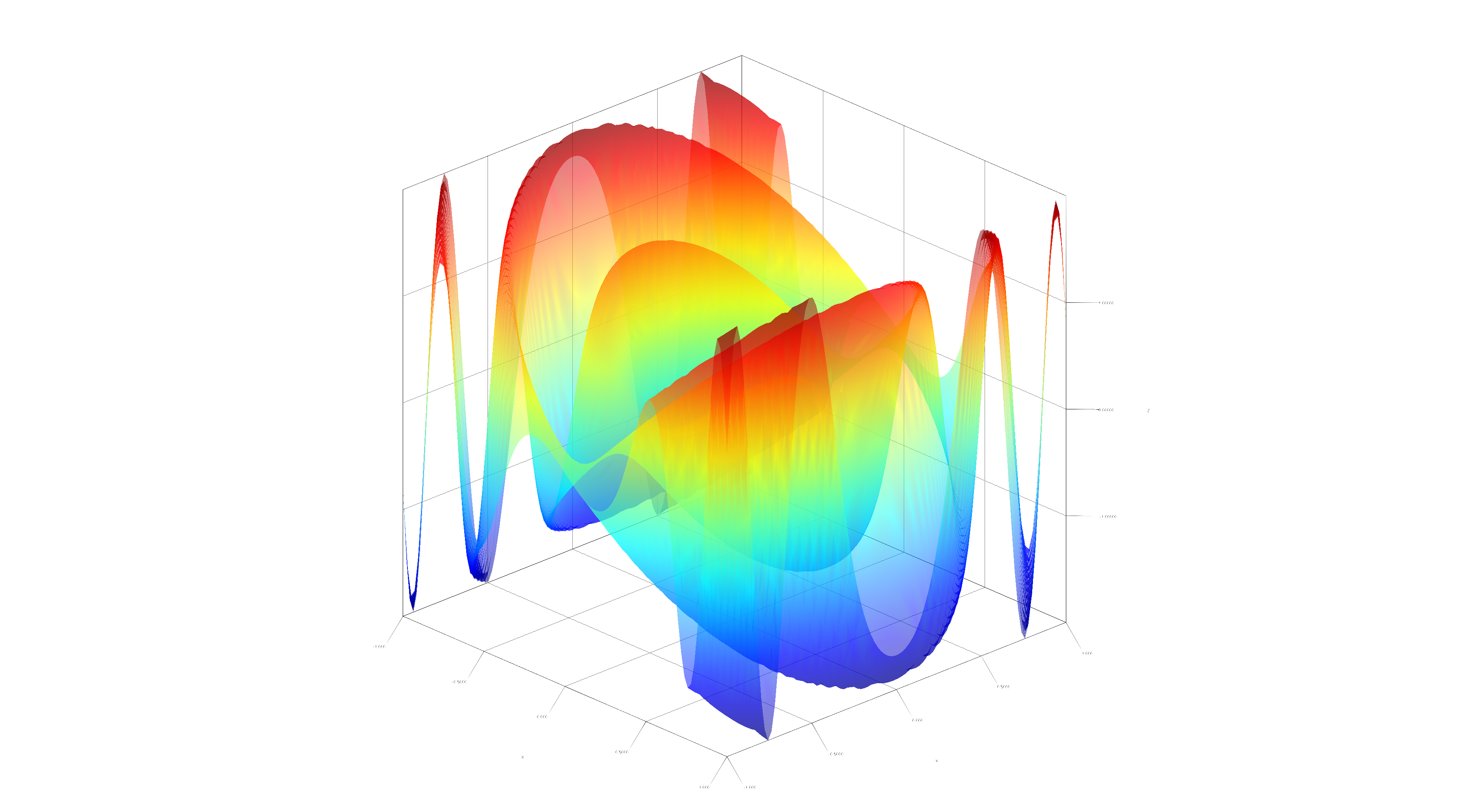
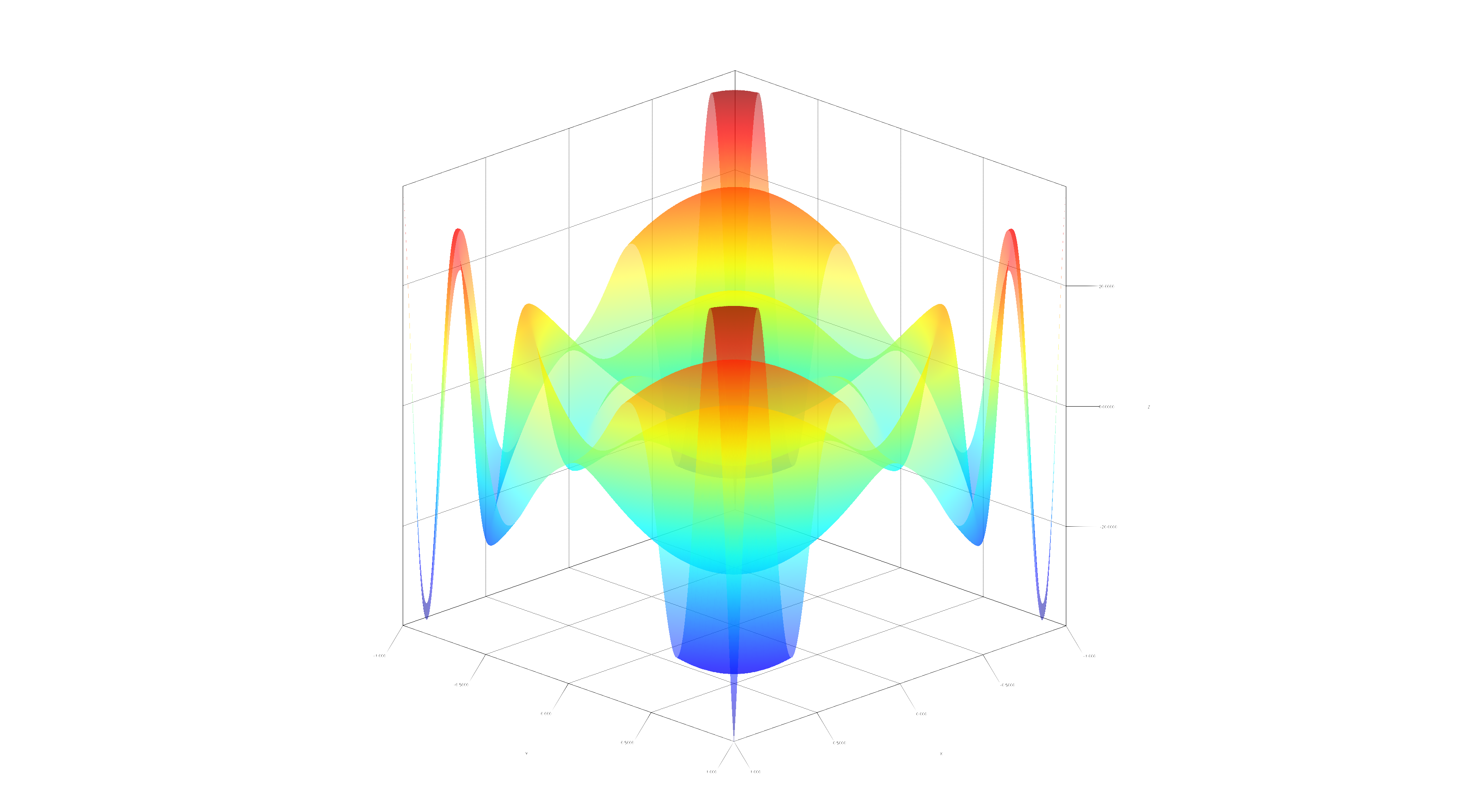
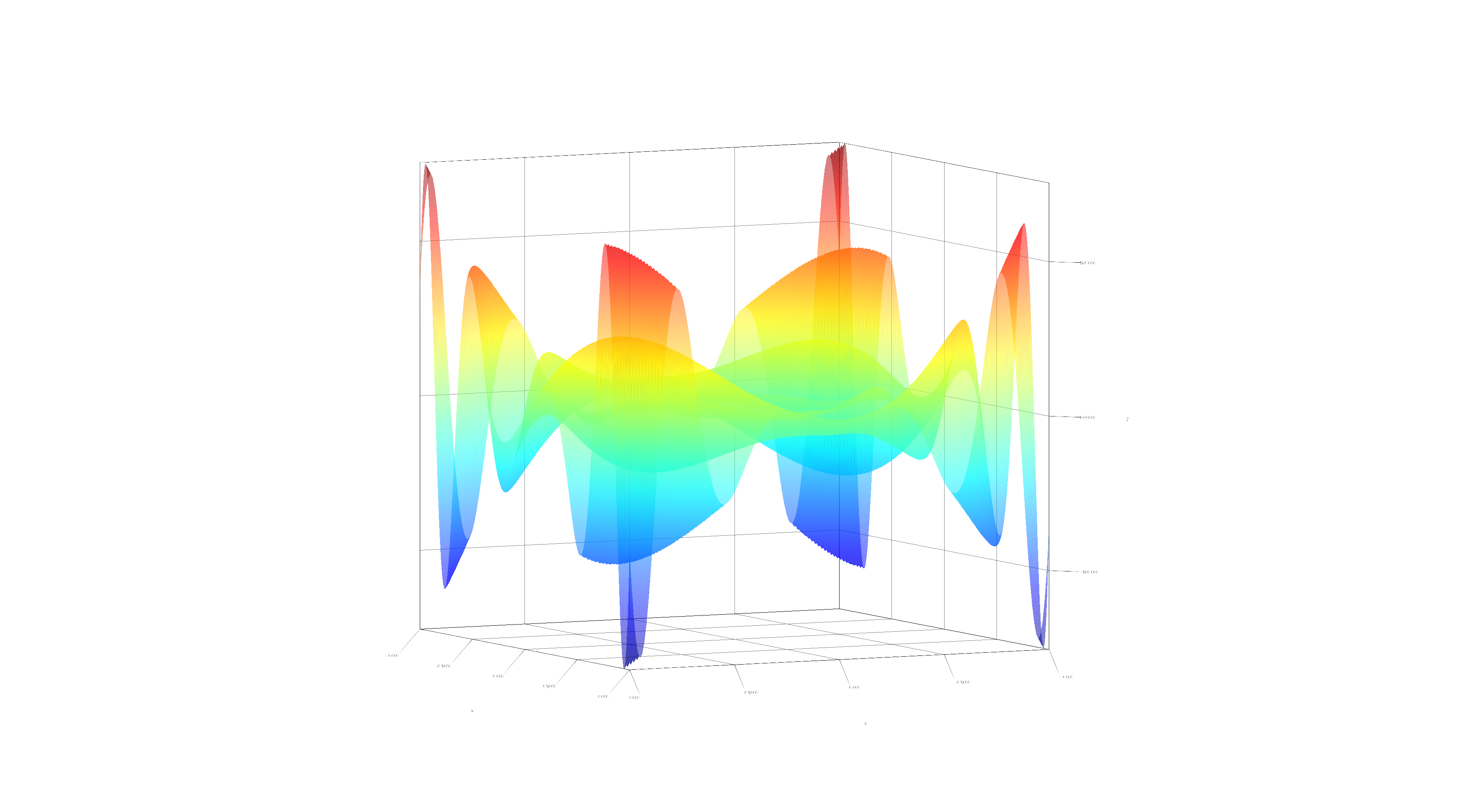
Plotting is also possible in higher dimensions, for example in 3D via ./gradlew Plot3D:
Gradient descent is one application for Kotlin∇. Below, is a typical loss curve of SGD on a multilayer perceptron:
To train the model, execute ./gradlew MLP from within the parent directory.
To run the tests, execute ../gradlew allTests from the core directory.
Kotlin∇ claims to eliminate certain runtime errors, but how do we know the proposed implementation is not incorrect? One method, borrowed from the Haskell community, is called property-based testing (PBT), closely related to metamorphic testing. Notable implementations include QuickCheck, Hypothesis and ScalaTest (ported to Kotlin in Kotest). PBT uses algebraic properties to verify the result of an operation by constructing semantically equivalent but syntactically distinct expressions, which should produce the same answer. Kotlin∇ uses two such equivalences to validate its AD implementation:
- Analytic differentiation: manually differentiate and compare the values returned on a subset of the domain with AD.
- Finite difference approximation: sample space of symbolic (differentiable) functions, comparing results of AD to FD.
For example, consider the following test, which checks whether the analytical derivative and the automatic derivative, when evaluated at a given point, are equal to each other within the limits of numerical precision:
val x by Var()
val y by Var()
val z = y * (sin(x * y) - x) // Function under test
val `∂z∕∂x` = d(z) / d(x) // Automatic derivative
val manualDx = y * (cos(x * y) * y - 1) // Analytical derivative
"∂z/∂x should be y * (cos(x * y) * y - 1)" {
NumericalGenerator.assertAll { ẋ, ẏ ->
// Evaluate the results at a given seed
val autoEval = `∂z∕∂x`(x to ẋ, y to ẏ)
val manualEval = manualDx(x to ẋ, y to ẏ)
// Should pass iff Δ(adEval, manualEval) < Ɛ
autoEval shouldBeApproximately manualEval
}
}PBT will search the input space for two numerical values ẋ and ẏ, which violate the specification, then "shrink" them to discover pass-fail boundary values. We can construct a similar test using finite differences:
"d(sin x)/dx should be equal to (sin(x + dx) - sin(x)) / dx" {
NumericalGenerator.assertAll { ẋ ->
val f = sin(x)
val `df∕dx` = d(f) / d(x)
val adEval = `df∕dx`(ẋ)
val dx = 1E-8
// Since ẋ is a raw numeric type, sin => kotlin.math.sin
val fdEval = (sin(ẋ + dx) - sin(ẋ)) / dx
adEval shouldBeApproximately fdEval
}
}Above, we compare numerical errors for three types of computational differentiation against infinite precision symbolic differentiation (IP):
- Finite precision automatic differentiation (AD)
- Finite precision symbolic differentiation (SD)
- Finite precision finite differences (FD)
AD and SD both exhibit relative errors (i.e. with respect to each other) several orders of magnitude lower than their absolute errors (i.e. with respect to IP), which roughly agree to within numerical precision. As expected, FD exhibits numerical error significantly higher than AD and SD due to the inaccuracy of floating-point division.
There are many other ways to independently verify the numerical gradient, such as dual numbers or the complex step derivative. Another method is to compare the numerical output against a well-known implementation, such as TensorFlow. We plan to conduct a more thorough comparison of numerical accuracy and performance.
To understand the core of Kotlin∇'s AD implementation, please refer to the scalar example.
This project relies on a few Kotlin-specific language features, which together enable a concise, flexible and type-safe user interface. The following features have proven beneficial to the development of Kotlin∇:
Operator overloading enables concise notation for arithmetic on abstract types, where the types encode algebraic structures, e.g., Group, Ring, and Field. These abstractions are extensible to other kinds of mathematical structures, such as complex numbers and quaternions.
For example, suppose we have an interface Group, which overloads the operators + and *, and is defined like so:
interface Group<T: Group<T>> {
operator fun plus(addend: T): T
operator fun times(multiplicand: T): T
}Here, we specify a recursive type bound using a method known as F-bounded quantification to ensure that operations return the concrete type variable T, rather than something more abstract like Group. Imagine a class Fun that has implemented Group. It can be used as follows:
fun <T: Group<T>> cubed(t: T): T = t * t * t
fun <T: Group<T>> twiceCubed(t: T): T = cubed(t) + cubed(t)Like Python, Kotlin supports overloading a limited set of operators, which are evaluated using a fixed precedence. In the current version of Kotlin∇, operators do not perform any computation, they simply construct a directed acyclic graph representing the symbolic expression. Expressions are only evaluated when invoked as a function.
With higher-order functions and lambdas, Kotlin treats functions as first-class citizens. This allows us to represent mathematical functions and programming functions with the same underlying abstractions (typed FP). Several recent papers have demonstrated the expressiveness of this paradigm for automatic differentiation.
In Kotlin∇, all expressions can be treated as functions. For example:
fun <T: Group<T>> makePoly(x: Var<T>, y: Var<T>) = x * y + y * y + x * x
val x by Var()
val y by Var()
val f = makePoly(x, y)
val z = f(1.0, 2.0) // Returns a value
println(z) // Prints: 7Additionally, it is possible to build functions consisting of varying dimensional inputs:
fun <T: Fun<T>> mlp(p1: VFun<T, D3>, p2: MFun<T, D3, D3>, p3: T) =
((p1 * p2 + p1 * p2 * p2 dot p1 + p1) - p3) pow p3Kotlin∇ uses operator overloading in the host language to first construct a dataflow graph, but evaluates the graph lazily. Called "multi-stage programming", or staging, this is a metaprogramming technique from the ML community which enables type-safe runtime code translation and compilation. More recently, staging has been put to effective use for compiling embedded DSLs similar to Kotlin∇.
In its current form, Kotlin∇ takes a "shallow embedding" approach. Similar to an interpreter, it adheres closely to the user-defined program and does not perform much code specialization or rewriting for optimization purposes. Unlike an interpreter, it postpones evaluation until all free variables in an expression have been bound. Consider the following snippet, which decides when to evaluate an expression:
var EAGER = false
operator fun invoke(newBindings: Bindings<X>): Fun<X> =
Composition(this, newBindings).run { if (bindings.complete || EAGER) evaluate() else this }If bindings are complete, this means there are no unbound variables remaining (implementation omitted for brevity), and we can evaluate the expression to obtain a numerical result. Suppose we have the following user code:
val x = Var()
val y = Var()
val z = Var()
val f0 = x + y * z
var f1 = f0(x to 1).also { println(it) } // Prints: (x + y * z)(x=1)
var f2 = f1(y to 2).also { println(it) } // Prints: (x + y * z)(x=1)(y=2)
var f3 = f2(z to 3).also { println(it) } // Prints: 7Once the last line is reached, all variables are bound, and instead of returning a Composition, Kotlin∇ evaluates the function, returning a constant. Alternatively, if EAGER mode is enabled, each invocation is applied as early as possible:
EAGER = true
f1 = f0(x to 1).also { println(it) } // Prints: 1 + y * z
f2 = f1(y to 2).also { println(it) } // Prints: 1 + 2 * z
f3 = f2(z to 3).also { println(it) } // Prints: 7In the following section, we describe how evaluation works.
Algebraic data types (ADTs) in the form of sealed classes (a.k.a. sum types) facilitate a limited form of pattern matching over a closed set of subclasses. By using these, the compiler forces us to provide an exhaustive control flow when type checking a sealed class. Consider the following classes:
class Const<T: Fun<T>>(val number: Number) : Fun<T>()
class Sum<T: Fun<T>>(val left: Fun<T>, val right: Fun<T>) : Fun<T>()
class Prod<T: Fun<T>>(val left: Fun<T>, val right: Fun<T>) : Fun<T>()
class Var<T: Fun<T>>: Fun<T>() { override val variables: Set<Var<X>> = setOf(this) }
class Zero<T: Fun<T>>: Const<T>(0.0)
class One<T: Fun<T>>: Const<T>(1.0)When checking the type of a sealed class, consumers must explicitly handle every case, as incomplete control flow will produce a compiler error rather than fail at runtime. Consider a simplified definition of the superclass Fun, which defines invocation and differentiation using a restricted form of pattern matching:
sealed class Fun<X: Fun<X>>(open val variables: Set<Var<X>> = emptySet()): Group<Fun<X>> {
constructor(vararg fns: Fun<X>): this(fns.flatMap { it.variables }.toSet())
// Since the subclasses of Fun are a closed set, no `else ...` is required.
operator fun invoke(map: Bindings<X>): Fun<X> = when (this) {
is Const -> this
is Var -> map.getOrElse(this) { this } // Partial application is permitted
is Prod -> left(map) * right(map) // Smart casting implicitly casts after checking
is Sum -> left(map) + right(map)
}
fun d(variable: Var<X>): Fun<X> = when(this) {
is Const -> Zero
is Var -> if (variable == this) One else Zero
// Product rule: d(u*v)/dx = du/dx * v + u * dv/dx
is Prod -> left.d(variable) * right + left * right.d(variable)
is Sum -> left.d(variable) + right.d(variable)
}
operator fun plus(addend: Fun<T>) = Sum(this, addend)
operator fun times(multiplicand: Fun<T>) = Prod(this, multiplicand)
}Symbolic differentiation as implemented by Kotlin∇ has two distinct passes, one for differentiation and one for evaluation. Differentiation constitutes a top-down substitution process on the computation graph and evaluation propagates the values from the bottom, up. This reduction semantics for this procedure are described more precisely in the specification.
Kotlin∇ functions are not only data structures, but Kotlin functions which can be invoked by passing a Bindings instance (effectively, a Map<Fun<X>, Fun<X>>). To enable this functionality, we overload the invoke operator, then recurse over the graph, using Bindings as a lookup table. If a matching subexpression is found, we propagate the bound value instead of the matching function. This is known as the interpreter pattern.
Kotlin's smart casting is an example of flow-sensitive type analysis where the abstract type Fun can be treated as Sum after performing an is Sum check. Without smart casting, we would need to write (this as Sum).left to access the member, left, causing a potential ClassCastException if the cast were mistaken.
By using extension functions, users can convert between numerical types in the host language and our eDSL, by augmenting classes with additional operators. Context-oriented programming, allows users to define custom extensions without requiring subclasses or inheritance.
data class Const<T: Group<T>>(val number: Double) : Fun()
data class Sum<T: Group<T>>(val e1: Fun, val e2: Fun) : Fun()
data class Prod<T: Group<T>>(val e1: Fun, val e2: Fun) : Fun()
class Fun<T: Group<T>>: Group<Fun<T>> {
operator fun plus(addend: Fun<T>) = Sum(this, addend)
operator fun times(multiplicand: Fun<T>) = Prod(this, multiplicand)
}
object DoubleContext {
operator fun Number.times(expr: Fun<Double>) = Const(toDouble()) * expr
}Now, we can use the context to define another extension, Fun.multiplyByTwo, which computes the product inside a DoubleContext, using the operator overload we defined above:
fun Fun<Double>.multiplyByTwo() = with(DoubleContext) { 2 * this } // Uses `*` operator in DoubleContextExtensions can also be defined in another file or context and imported on demand. For example, Kotlin∇ also uses extensions to define shape-safe constructors and operators for vector and matrix arithmetic.
In conjunction with ADTs, Kotlin∇ also uses multiple dispatch to instantiate the most specific result type of applying an operator based on the type of its operands. While multiple dispatch is not an explicit language feature, it can be emulated using inheritance.
Building on the previous example, a common task in AD is to simplify a graph. This is useful in order to minimize the total number of calculations required, improving numerical stability. We can eagerly simplify expressions based on algebraic rules of replacement. Smart casting allows us to access members of a class after checking its type, without explicitly casting it:
override fun times(multiplicand: Function<X>): Function<X> = when {
this == zero -> this
this == one -> multiplicand
multiplicand == one -> this
multiplicand == zero -> multiplicand
this == multiplicand -> pow(two)
this is Const && multiplicand is Const -> const(value * multiplicand.value)
// Further simplification is possible using rules of replacement
else -> Prod(this, multiplicand)
}
val result = Const(2.0) * Sum(Var(2.0), Const(3.0)) // Sum(Prod(Const(2.0), Var(2.0)), Const(6.0))This allows us to put all related control flow on a single abstract class which is inherited by subclasses, simplifying readability, debugging and refactoring.
While first-class dependent types are useful for ensuring arbitrary shape safety (e.g., when concatenating and reshaping matrices), they are unnecessary for simple equality checking (such as when multiplying two matrices). When the shape of a tensor is known at compile-time, it is possible to encode this information using a less powerful type system*, as long as it supports subtyping and parametric polymorphism (a.k.a. generics). In practice, we can implement a shape-checked tensor arithmetic in languages like Java, Kotlin, C++, C# or Typescript, which accept generic type parameters. In Kotlin, whose type system is less expressive than Java, we use the following strategy.
Shape safety is currently supported up to rank-2 tensors, i.e. matrices. To perform dimension checking in our type system, we first enumerate a list of integer type literals as a chain of subtypes, C <: C - 1 <: C - 2 <: ... <: 1 <: 0, where C is the largest fixed-length dimension we wish to represent, which can be specified by the user prior to compilation. This guarantees linear space and time complexity for subtype checking, with a constant upper bound.
@file:Suppress("ClassName")
interface Nat<T: D0> { val i: Int } // Used for certain type bounds
sealed class D0(open val i: Int = 0) { companion object: D0(), Nat<D0> }
sealed class D1(override val i: Int = 1): D0(i) { companion object: D1(), Nat<D1> }
sealed class D2(override val i: Int = 2): D1(i) { companion object: D2(), Nat<D2> }
sealed class D3(override val i: Int = 3): D2(i) { companion object: D3(), Nat<D3> }
//... † Automatically generatedNext, we overload the call operator to emulate instantiating a collection literal, using arity to infer its dimensionality. Consider the rank-1 case for length inference on vector literals:
open class Vec<E, Len: D1>(val contents: List<E>)
fun <T> Vec(t1: T): Vec<T, D1> = Vec(listOf(t1))
fun <T> Vec(t1: T, t2: T): Vec<T, D2> = Vec(listOf(t1, t2))
fun <T> Vec(t1: T, t2: T, t3: T): Vec<T, D3> = Vec(listOf(t1, t2, t3))
//... † Automatically generatedFinally, we encode length as a parameter of the operand type. Since integer literals are a chain of subtypes, we need only define one operator using the highest literal, and can rely on Liskov substitution to preserve shape safety for all subtypes.
infix operator fun <C: D1, V: Vec<Int, C>> V.plus(v: V): Vec<Int, C> =
Vec(contents.zip(v.contents).map { it.first + it.second })The operator + can now be used like so. Incompatible operands will cause a type error:
val one = Vec(1, 2, 3) + Vec(1, 2, 3) // Always runs safely
val add = Vec(1, 2, 3) + Vec(listOf(/*...*/)) // May fail at runtime
val sum = Vec(1, 2) + add // Does not compileA similar syntax is available for matrices and higher-rank tensors. For example, Kotlin∇ can infer the shape of multiplying two matrices, and will not compile if their inner dimensions do not match:
open class Mat<X, R: D1, C: D1>(vararg val rows: Vec<X, C>)
fun <X> Mat1x2(d0: X, d1: X): Mat<X, D1, D2> = Mat(Vec(d0, d1))
fun <X> Mat2x1(d0: X, d1: X): Mat<X, D2, D1> = Mat(Vec(d0), Vec(d1))
//... † Automatically generated
operator fun <Q: D1, R: D1, S: D1> Mat<Int, Q, R>.times(m: Mat<Int, R, S>): Mat<Int, Q, S> = TODO()
// Inferred type: Mat<Int, D4, D4>
val l = Mat4x4(
1, 2, 3, 4,
5, 6, 7, 8,
9, 0, 0, 0,
9, 0, 0, 0
)
// Inferred type: Mat<Int, D4, D3>
val m = Mat4x3(
1, 1, 1,
2, 2, 2,
3, 3, 3,
4, 4, 4
)
// Inferred type: Mat<Int, D4, D3>
val lm = l * m
// m * m // Compile error: Expected Mat<3, *>, found Mat<4, 3>Further examples are provided for shape-safe matrix operations such as addition, subtraction and transposition.
A similar technique is possible in Haskell, which is capable of a more powerful form of type-level computation, type arithmetic. Type arithmetic makes it easy to express convolutional arithmetic and other arithmetic operations on shape variables (say, splitting a vector in half), which is currently not possible, or would require enumerating every possible combination of type literals.
∗ Many type systems are still capable of performing arbitrary computation in the type checker. As specified, Java's type system is known to be Turing Complete. It may be possible to emulate a limited form of dependent types in Java by exploiting this property, although this may not be computationally tractable due to the practical limitations noted by Grigore.
† Statically generated code, shipped within the library. To regenerate these methods (e.g., using larger dimensions), a code generator is provided.
Kotlin∇ programs are staged into Kaliningraph, an experimental IR for graph computation. As written by the user, many graphs are computationally suboptimal due to expression swell and parameter sharing. To accelerate forward- and backpropagation, it is often advantageous to simplify the graph by applying the reduction semantics in a process known as graph canonicalization. Kaliningraph enables compiler-like optimizations over the graph such as expression simplification and analytic root-finding, and supports features for visualization and debugging, e.g., in computational notebooks.
Property delegation is a reflection feature in the Kotlin language which lets us access properties to which an instance is bound. For example, we can read the property name like so:
class Var(val name: String?) {
operator fun getValue(thisRef: Any?, property: KProperty<*>) = Var(name ?: property.name)
}This feature allows consumers to instantiate variables e.g., in an embedded DSL without redeclaring their names:
val x by Var() // With property delegation
val x = Var("x") // Without property delegationWithout property delegation, users would need to repeat the property name in the constructor.
The current API is stable but can be improved in many ways. Currently, Kotlin∇ does not infer a function's input dimensionality (i.e. free variables and their corresponding shape). While it is possible to perform variable capture over a small alphabet using type safe currying, this technique incurs a large source code overhead. It may be possible to reduce the footprint using phantom types or some form of union type bound (cf. Kotlin, Java).
When the shape of an N-dimensional array is known at compile-time, we can use type-level integers to ensure shape conforming tensor operations (inspired by Nexus and others).
Allowing users to specify a matrix's structure in its type signature, (e.g., Singular, Symmetric, Orthogonal, Unitary, Hermitian, Toeplitz) would allow us to specialize derivation over such matrices (cf. section 2.8 of The Matrix Cookbook).
Computers appear to be very complicated machines. Beneath this complexity lies a remarkably simple idea: many apparently complex routines can be rewritten in terms of function composition. Consider the binary operator ^, which can be lowered as follows:
a ^ b := a * ... * a
\_________/
b times
a * b := a + ... + a
\_________/
b times
a + b := a + 1 + ... + 1
\_________/
b times
a := next*(next(...next(1)...))
\________________/
a times
∗ next is also called S in Peano arithmetic.
By using the λ-calculus, Church tells us, we can lower a large portion of mathematics onto a single operator: function application. Curry, by way of Schönfinkel, gives us combinatory logic, a kind of Rosetta stone for deciphering and translating between a host of cryptic languages. These two ideas, λ-calculus and combinators, are keys to unlocking many puzzles in computer science and mathematics.
Though mathematically elegant, Church numerals are not particularly efficient or pleasant to read. One discovers that trying to encode Church arithmetic in a language without dependent types grows quickly impractical. By selecting a higher radix, however, it is possible to reduce spatial complexity and improve readability, albeit at the cost of increased temporal complexity on certain operations (e.g., + and -). Kotlin∇ uses a binary encoding by default, however generators for other bases are also provided for convenience.
The trouble with numerical towers is that they assume all inheritors are aware of the tower. In practice, many types we would like to reuse are entirely oblivious to our DSL. How do we allow users to bring in existing types without needing to modify their source code? This kind of ad hoc polymorphism can be achieved using a pattern called the type class. While the JVM does not allow multiple inheritance on classes, it does support multiple inheritance and default methods on interfaces, allowing users to implement an interface via delegation rather than inheritance.
Suppose we have a base type, Nat defined as an interface with a unitary member, nil, and its successor function, next, representing the Church encoding for natural numbers. To emulate instantiation, we can provide a nested class equipped with a constructor overriding nil and next as follows:
interface Nat<T> {
val nil: T
val one: T get() = nil.next()
fun T.next(): T
class of<T>(
override val nil: T,
val vnext: T.() -> T
): Nat<T> {
override fun T.next(): T = vnext()
}
}Now, if we wanted to wrap an external type, such as Double, inside our tower, we could do so as follows:
val doubleNat = Nat.of(nil = 0.0) { this + 1.0 }Although the Nat interface is very expressive, evaluating arithmetic expressions on Nats can be computationally expensive. For instance, we could define the first three hyperoperations naïvely as follows:
tailrec fun <T> Nat<T>.plus(l: T, r: T, acc: T = l, i: T = nil): T =
if (i == r) acc else plus(l, r, acc.next(), i.next())
tailrec fun <T> Nat<T>.times(l: T, r: T, acc: T = nil, i: T = nil): T =
if (i == r) acc else times(l, r, acc + l, i.next())
tailrec fun <T> Nat<T>.pow(base: T, exp: T, acc: T = one, i: T = one): T =
if (i == exp) acc else pow(base, exp, acc * base, i.next())However, we note that computing pow(a, b) using this representation requires 𝓞(a↑b) operations using Knuth notation. Clearly, we must do better if this encoding is to be usable. We can make Nat more efficient by introducing a subtype, Group, which forces implementors to define a native addition operator:
interface Group<T>: Nat<T> {
override fun T.next(): T = this + one
override fun T.plus(t: T): T
class of<T>(
override val nil: T, override val one: T,
val plus: (T, T) -> T
): Group<T> {
override fun T.plus(t: T) = plus(this, t)
}
}Given a Group, we can now define a more efficient implementation of Fibonacci. This will use the group-specific addition operator:
tailrec fun <T> Nat<T>.fibonacci(
n: T,
seed: Pair<T, T> = nil to one,
fib: (Pair<T, T>) -> Pair<T, T> = { (a, b) -> b to a + b },
i: T = nil,
): T =
if (i == n) fib(seed).first
else fibonacci(n = n, seed = fib(seed), i = i.next())
val doubleGroup = Group.of(one = 1.0, plus = { a, b -> a + b })
println(doubleGroup.fibonacci(10.0)) // Prints: 233.0We could further extend this chain by introducing a subtype called Ring, which overrides + and requires implementors to define a native * operator. Rings and their relatives are known to have many useful applications in graph theory and statistics:
interface Ring<T>: Group<T> {
override fun T.plus(t: T): T
override fun T.times(t: T): T
class of<T>(
override val nil: T, override val one: T,
val plus: (T, T) -> T,
val times: (T, T) -> T
): Ring<T> {
override fun T.plus(t: T) = plus(this, t)
override fun T.times(t: T) = times(this, t)
}
}
val doubleRing = Ring.of(one = 1.0, plus = { a, b -> a + b }, times = { a, b -> a * b })Since differentiation is a linear map between function spaces, we now have the primitives necessary to build a fully-generic AD system, and could easily implement the sum and product rules. To view the above example in full, see Types.kt.
What benefit does this abstraction provide to the end user? By parameterizing over primitive operators, Kotlin∇ consumers can easily swap out a tensor backend without needing to alter or recompile any upstream dependencies. This feature makes multiplatform development a breeze: wherever a type class operator (e.g., + or *) with matching signature is encountered across a project, it will be dispatched to the user-supplied lambda delegate for specialized execution on custom hardware. Runtime indirection can be elided with proper compiler inlining for zero-cost abstraction.
By default, Kotlin∇ supports compile time type arithmetic in the following domain:
- Fully symmetric arithmetic:
{ a ⍟ b ϵ [0..16){+,-,*}[0..16) | 0 ≤ a ⍟ b } - Asymmetric arithmetic:
{ a ⍟ b ϵ [0..512){+,-}[0..16) | 0 ≤ a ⍟ b < 512 } - Semi-symmetric arithmetic:
{ a / b = c, a = b * c | a, b, c ϵ [0..128) & a % b = 0 }
Arithmetic outside this domain is checked at runtime, prior to evaluation.
Compile time type arithmetic is achieved by generating a type-level representation of the Church encoding. A usage example is shown in ChurchArithmeticTest.kt, which may be run with the following command:
./gradlew :kotlingrad:cleanJvmTest :kotlingrad:jvmTest --tests "ai.hypergraph.kotlingrad.typelevel.church.ChurchArithmeticTest"Extensions to other bases, including binary and decimal are also provided, which may be used as follows:
// Boolean arithmetic
val b32 = T.F
.let { it + T.F } // B_4<Ø>
.let { it + T.F.F } // B_8<Ø>
.let { it + T.T } // T<T<F<T<Ø>>>>
.let { it + T.F } // T<F<T<T<Ø>>>>
.let { it - T.F } // T<T<F<T<Ø>>>>
.let { it + T.F } // T<F<T<T<Ø>>>>
.let { it + T.F } // T<T<T<T<Ø>>>>
.let { it + T } // T<F<F<F<Ø>>>>
assertEquals(T.F.F.F.F, b32)
// Chinese arithmetic
val 四十二 = (十七 减 九)
.let { it 加 it } // 六<一<无>>
.let { (it 加 八) 加 六 } // 零<三<无>>
.let { (it 减 三) 加 九 } // 六<三<无>>
.let { (it 加 六) 除 六 } // 七<无>
.let { (it 乘 六) 加 五 } // 七<四<无>>
.let { (it 减 三) 减 九 } // 五<三<无>>
.let { (it 加 五) 加 二 } // 二<四<无>>
.also { assertEquals(六 乘 七, it) }
assertEquals(42, 四十二.toInt())To alter the arithmetic domain, edit the file BinGen.kt/算盘厂.kt, then use the following command to regenerate Arithmetic.kt/算盘.kt:
./gradlew genShapesIn practice, compile time type arithmetic may struggle to compute numbers in excess of 4095. The Kotlin team has been informed of these issues:
This API is experimental and subject to change without notice. In the future, it will be used to statically type check tensor functions whose output shape is an arithmetic function of the input shapes, e.g., concatenation, splitting and convolution.
For a detailed grammar and semantics, please refer to the Kotlin∇ specification.
The following graph depicts the subtyping relation between classes and interfaces in Kotlin∇.
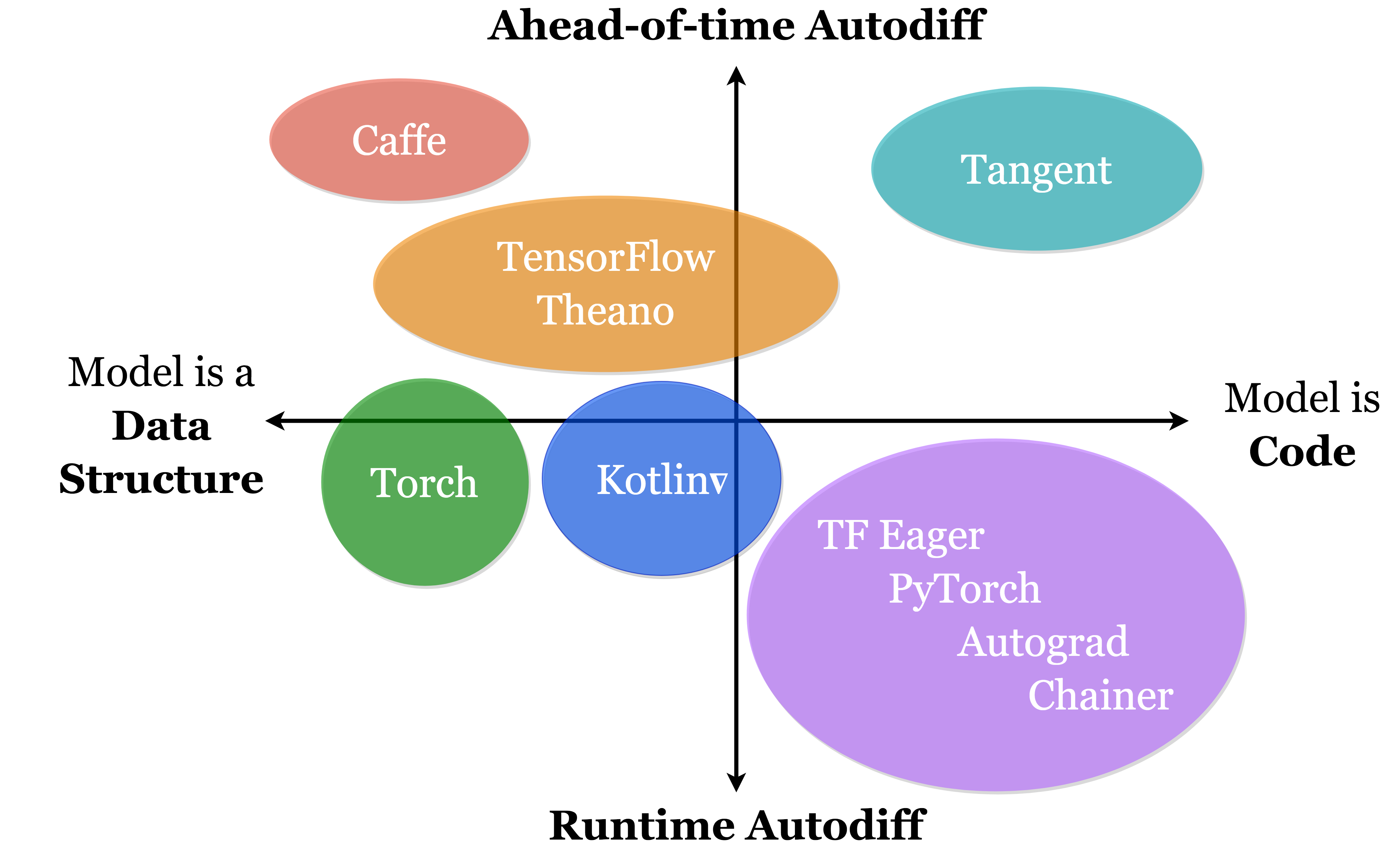
Unlike certain frameworks which simply wrap an existing AD library in a type-safe DSL, Kotlin∇ contains a fully shape-safe implementation of algorithmic differentiation, written in pure Kotlin. By doing so, it can leverage Kotlin language features such as typed functional programming, as well as interoperability with other languages on the JVM platform. Furthermore, it implements symbolic differentiation, which unlike Wengert tape or dual-number based ADs, allows it to calculate derivatives of arbitrarily high order with zero extra engineering required. Further details can be found below.
| Framework | Language | SD¹ | AD² | HD³ | DP⁴ | FP⁵ | TS⁶ | SS⁷ | DT⁸ | MP⁹ |
|---|---|---|---|---|---|---|---|---|---|---|
| Kotlin∇ | Kotlin | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | 🚧 | ✔️ |
| DiffSharp | F# | ❌ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ❌ | ❌ | ❌ |
| TensorFlow.FSharp | F# | ❌ | ❌ | ❌ | ✔️ | ✔️ | ✔️ | ✔️ | ❌ | ❌ |
| shapesafe | Scala | 🚧 | 🚧 | 🚧 | 🚧 | ✔️ | ✔️ | ✔️ | 🚧 | ❌ |
| Nexus | Scala | ❌ | ✔️ | ❌ | ✔️ | ✔️ | ✔️ | ✔️ | ❌ | ❌ |
| Lantern | Scala | ❌ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ❌ | ❌ | ❌ |
| Hipparchus | Java | ❌ | ✔️ | ❌ | ❌ | ❌ | ✔️ | ❌ | ❌ | ❌ |
| JAutoDiff | Java | ✔️ | ✔️ | ❌ | ❌ | ❌ | ✔️ | ❌ | ❌ | ❌ |
| Eclipse DL4J | Java | ❌ | 🚧 | ❌ | ❌ | ❌ | ✔️ | ❌ | ❌ | ❌ |
| SICMUtils | Clojure | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ❌ | ❌ | ❌ | ❌ |
| Halide | C++ | ❌ | ✔️ | ✔️ | ✔️ | ❌ | ✔️ | ❌ | ❌ | ❌ |
| Tensor Safe | Haskell | ❌ | ❌ | ❌ | ❌ | ✔️ | ✔️ | ✔️ | ✔️ | ❌ |
| HaskTorch | Haskell | ❌ | ❌ | ❌ | ❌ | ✔️ | ✔️ | ✔️ | ❌ | ❌ |
| Dex | Haskell | ❌ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | 🚧 | ❌ |
| Grenade | Haskell | ❌ | ❌ | ❌ | ❌ | ✔️ | ✔️ | ✔️ | ❌ | ❌ |
| Stalin∇ | Scheme | ❌ | ✔️ | ❌ | ❌ | ✔️ | ❌ | ❌ | ❌ | ❌ |
| Myia | Python | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ❌ | ❌ | ❌ | 🚧 |
| Autograd | Python | ❌ | ✔️ | ❌ | ❌ | ❌ | ❌ | ❌ | ❌ | ❌ |
| JAX | Python | ❌ | ✔️ | ✔️ | ✔️ | ✔️ | ❌ | ❌ | ❌ | 🚧 |
| Tangent | Python | ❌ | ✔️ | ❌ | ❌ | ❌ | ❌ | ❌ | ❌ | ❌ |
| Analitik | Analitik | ✔️ | ❌ | ❌ | ❌ | ✔️ | ❌ | ❌ | ❌ | ❌ |
¹ Symbolic differentiation*, ² Automatic differentiation*, ³ Higher-order/rank differentiation, ⁴ Differentiable programming*, ⁵ Functional programming, ⁶ Compile-time type safety, ⁷ Compile-time shape safety, ⁸ Dependently Typed, ⁹ Multiplatform
∗ Although we do not distinguish between AD and SD, here we adopt the authors' preferred nomenclature. We do make a distinction between differentiable programming libraries and those which simply construct neural networks. The 🚧 symbol indicates work in progress.
To the author's knowledge, Kotlin∇ is the first AD implementation in native Kotlin. While the particular synthesis of these ideas (i.e. shape-safe, functional AD, using generic types) is unique, it has been influenced by a long list of prior work in AD. Below is a list of projects and publications that helped inspire this work.
- The Simple Essence of Automatic Differentiation
- Reverse-Mode AD in a Functional Framework: Lambda the Ultimate Backpropagator
- Automatic differentiation in ML: Where we are and where we should be going
- A Leibniz Notation for Automatic Differentiation
- First-Class Automatic Differentiation in Swift: A Manifesto
- The (JAX) Autodiff Cookbook
- Automatic Differentiation in PyTorch
- Automatic Differentiation in Machine Learning: a Survey
- Complexity of Derivatives Generated by Symbolic Differentiation
- Eigen-AD: Algorithmic Differentiation of the Eigen Library
- Fast parallel computation of polynomials using few processors, Valiant and Skyum (1983)
- The complexity of partial derivatives, Baur and Strassen (1983)
- Lower Bounds on Arithmetic Circuits via Partial Derivatives
- Learning Restricted Models of Arithmetic Circuits
- Neural Networks, Types, and Functional Programming
- Backpropagation with Continuation Callbacks: Foundations for Efficient and Expressive Differentiable Programming
- Backprop as Functor: A compositional perspective on supervised learning
- Demystifying Differentiable Programming: Shift/Reset the Penultimate Backpropagator
- Efficient Differentiable Programming in a Functional Array-Processing Language
- Operational Calculus for Differentiable Programming
- Differentiable Functional Programming
- Differentiable Programming for Image Processing and Deep Learning in Halide
- Software 2.0
- The Matrix Calculus You Need For Deep Learning, Parr and Howard (2018)
- Backpropagation in matrix notation, Mishachev (2017)
- Matrix derivatives, from the Matrix Cookbook
- Div, Grad, Curl and All That, Petersen and Pedersen (2012)
- Matrix Differentiation (and some other stuff), Barnes (2006)
- Symbolic Matrix Derivatives, Dwyer and Macphail (1948)
- Towards an API for the real numbers, Boehm (2020)
- miniKanren as a Tool for Symbolic Computation in Python, Willard (2020)
- A Design Proposal for an Object Oriented Algebraic Library, Niculescu (2003)
- On Using Generics for Implementing Algebraic Structures, Niculescu (2011)
- How to turn a scripting language into a domain-specific language for computer algebra, Jolly and Kredel (2008)
- Evaluation of a Java Computer Algebra System, Kredel (2007)
- Typesafe Abstractions for Tensor Operations, Chen (2017)
- Einstein Summation in Numpy, Bilaniuk (2016)
- Issues in Computer Algebra, Nunes-Harwitt
- Term Rewriting and All That, Baader and Nipkow (1998)
- Describing the syntax of programming languages using conjunctive and Boolean grammars, Okhotin (2016)
- Formal languages over GF(2), Okhotin (2019)
- KMath - Kotlin mathematics extensions library
- SymJa - Computer algebra language & symbolic math library for Android
- tensor - Linear algebra for tensors with symbolic and numeric scalars
- Hipparchus - An efficient, general-purpose mathematics components library in the Java programming language
- miniKanren - A tool for symbolic computation and logic programming
- SymJava - A Java library for fast symbolic-numeric computation
- JAS - Java Algebra System
- jalgebra - An abstract algebra library for Java
- COJAC - Numerical sniffing tool and Enriching number wrapper for Java
- chebfun - Allows representing functions as Chebyshev polynomials, for easy symbolic differentiation (or integration)
- horeilly1101/deriv - Open source derivative calculator REST API (and Java library)
- Hacker's Guide to Neural Networks, Karpathy (2014)
- Tricks from Deep Learning, Baydin et al. (2016)
- Practical Dependent Types in Haskell: Type-Safe Neural Networks, Le (2016)
- A guide to convolutional arithmetic for deep learning, Dumoulin and Visin (2018)
- Generalized Algebraic Data Types and Object-Oriented Programming, Kennedy and Russo (2005)
- Java Generics are Turing Complete, Grigore (2016)
- Dimension Types, Kennedy (2004)
- An algebraic view of dimension types, Kennedy (1996)
- Type Inference and Unification
- Constructive mathematics and computer programming, Martin-Lof (1984)
- Programming in Martin-Löf's Type Theory, Nordstrom et al. (1990)
- Compiling Embedded Languages, Elliott et al. (2003)
- Implicit Staging of EDSL Expressions: A Bridge between Shallow and Deep Embedding, Scherr and Chiba (2014)
- DSL Implementation Using Staging and Monads Sheard et al. (1999)
- Deeply Reifying Running Code for Constructing a Domain-Specific Language, Chiba et al. (2016)
- Staged Abstract Interpreters, Wei et al. (2019)
- Generating Fluent Embedded Domain-Specific Languages with Subchaining, Nakamaru et al. (2019)
- Generating a Generic Fluent API in Java, Nakamarua and Chiba (2020)
- Fling – A Fluent API Generator, Gil and Roth (2019)
- Scripting an IDE for EDSL awareness, Sergey et al. (2011)
- DeepTest: Automated Testing of Deep-Neural-Network-driven Autonomous Cars, Tian et al. (2018)
- QuickCheck: A Lightweight Tool for Random Testing of Haskell Programs, Claessen and Hughes (2000)
- Learning to Discover Efficient Mathematical Identities, Zaremba et al. (2014)
- TensorFlow.FSharp: An eDSL for writing numerical models in F# with support for interactive tensor shape-checking
- Stalin∇, a brutally optimizing compiler for the VLAD language, a pure dialect of Scheme with first-class automatic differentiation operators
- Autograd - Efficiently computes derivatives of NumPy code
- Myia - SCT based AD, adapted from Pearlmutter & Siskind's "Reverse Mode AD in a functional framework"
- JAX - Composable transformations of Python+NumPy programs: differentiate, vectorize, JIT to GPU/TPU, and more
- Dex - Research language for array processing in the Haskell/ML family
- Nexus - Type-safe tensors, deep learning and probabilistic programming in Scala
- Tangent - "Source-to-Source Debuggable Derivatives in Pure Python"
- Grenade - composable, dependently typed, practical, and fast RNNs in Haskell
- Lantern - a framework in Scala, based on delimited continuations and multi-stage programming
- JAutoDiff - An Automatic Differentiation Library
- DiffSharp, a functional AD library implemented in the F# language
- Analitik - Algebraic language for the description of computing processes using analytical transformations
The following individuals have helped shape this project through their enthusiasm and thoughtful feedback. Please check out their work.