A Mathematical Model of HIV Infections and Vaccination against the Development of AIDS
Final project for the course Mathematical Modeling in the Life Sciences.
Abstract
The human immunodeficiency virus (HIV) is a retrovirus that at- tacks human's immune system and leads to the consequent disease AIDS. Major features after the infection of HIV include salient anti- genic variation of the virus and a long incubation period (on average 8-10 years) before AIDS is finally induced. These features are close- ly associated with some features of HIV, the most important one of which may be the high mutation capability of the virus. Martin A. Nowak and Robert M. May studied the mathematical model of antigenic variation and diversiry threshold during HIV infec- tions, which was published on a paper in 1991 [1]. Later, on the basis of this model, Nowak and Angela R. Mclean discussed and analyzed the vaccination against HIV mathematically [2]. In our work, we will follow and repeat the most contents of the two papers and have some discussions about the mathematical model.
Selected Figures
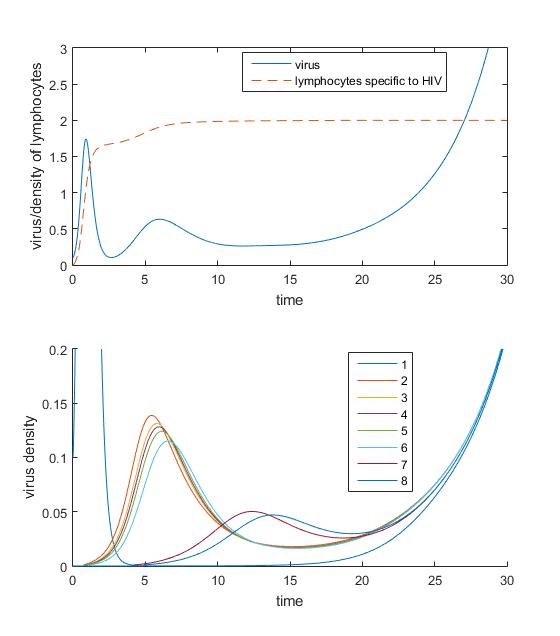
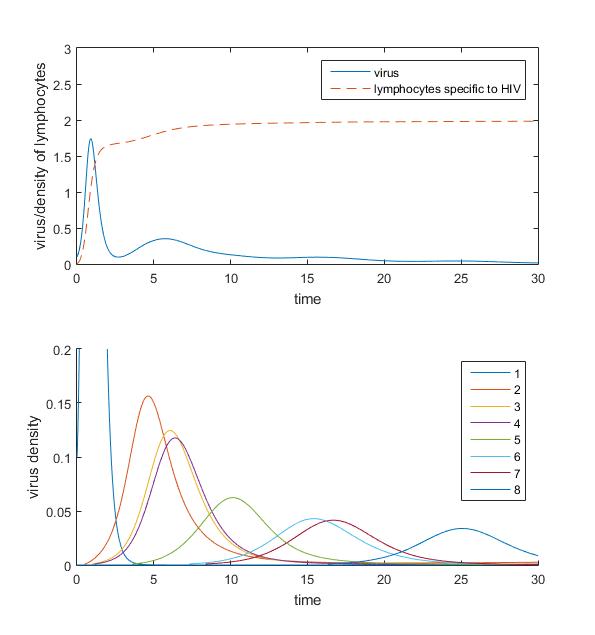
These figures are basic simulation plots for a dynamic system, modeling lymphocytes fighting against HIVs. In the system, a virus strand may generate other strands (mutants). The above figures are simulated with higher virus birth rate, these viruses finally escape the immune response. In contrast, the below results show that the viruses are eliminated with relatively lower birth rate.
For details and discussions see the report.
References
[1] Nowak M A, May R M. Mathematical biology of HIV infections: antigenic variation and diversity threshold[J]. Mathematical Biosciences, 1991, 106(1):1-21.
[2] Nowak M A, Mclean A R. A mathematical model of vaccination against HIV to prevent the development of AIDS.[J]. Proceedings of the Royal Society B Biological Sciences, 1991, 246(1316):141-6.