A pure-Python, PyTorch-like automatic differentiation library for education.

File Structure

.
├── match               # The Match library
│  ├── __init__.py      # --- contains default import statements
│  ├── list2d.py        # --- a storage class for matrix data
│  ├── matrix.py        # --- a 2D matrix class (including autodiff)
│  └── nn.py            # --- higher-level neural network functionality
├── demo_linear.ipynb   # A linear model demo (Jupyter)
├── demo_linear.py      # A linear model demo (script)
├── test.py             # Unit-tests for correctness
├── LICENSE             # MIT License
└── README.md           # This document

Demos

Although Match does not have any dependencies, the demos do. Demos import matplotlib, but you can skip (or comment) plotting cells (code) and not miss out on much. Demos come in two flavors: Jupyter Notebooks and Python scripts. These files are synced using Jupytext.

demo_linear_1d.mp4

Implementation of Automatic Differentiation

The library uses implements reverse-mode automatic differentiation. Here are highlights of the implementation:

list2d.py contains an implementation of several matrix operations (e.g., element-wise arithmetic, matrix multiplication, etc.)
matrix.py relies on list2d.py and adds automatic differentiation functionality (it was important to decouple the underlying matrix operations in list2d.py from the usage of Matrix objects; this made it easier to include matrix operations in the gradient functions without running into a recursive loop)
nn.py adds common neural network functionality on top of matrix.py

Single "`_`" Convention

You'll see some methods with a trailing _ in the name. This denotes that the method will mutate the current object. For example,

class List2D(object):

    ...

    def ones_(self) -> None:
        """Modify all values in the matrix to be 1.0."""
        self.__set(1.0)

    ...

    def relu(self) -> List2D:
        """Return a new List2D object with the ReLU of each element."""
        vals = [
            [max(0.0, self.vals[i][j]) for j in range(self.ncol)]
            for i in range(self.nrow)
        ]
        return List2D(*self.shape, vals)

    ...

The ones_ method sets all values of the current List2D to 1.0 whereas the relu method returns a new List2D object where each value is computed using relu function.

Double "`__`" Convention

Some method names start with two _. These are internal functions that should not be used outside of the class. For example,

class List2D(object):

    ...

    def __set(self, val) -> None:
        """Internal method to set all values in the matrix to val."""
        self.vals = [[val] * self.ncol for _ in range(self.nrow)]

    ...

You'll also find many double _ methods. These are known as Python magic or "dunder" (double underscore) methods. They make it easy to implement things like addition and subtraction with a custom object. For example,

class List2D(object):

    ...

    def __add__(self, rhs: float | int | List2D) -> List2D:
        """Element-wise addition: self + rhs."""
        return self.__binary_op(add, rhs)

    ...

a = List2D(...)
b = List2D(...)
c = a + b # <-- uses the __add__ method with self=a and rhs=b

Compute Graphs

Consider the following model:

class MatchNetwork(match.nn.Module):
    def __init__(self, n0, n1, n2) -> None:
        super().__init__()
        self.linear1 = match.nn.Linear(n0, n1)
        self.relu = match.nn.ReLU()
        self.linear2 = match.nn.Linear(n1, n2)
        self.sigmoid = match.nn.Sigmoid()

    def forward(self, x) -> Matrix:
        x = self.linear1(x)
        x = self.relu(x)
        x = self.linear2(x)
        x = self.sigmoid(x) # <-- this line of code is referenced below
        return x

What happens we we create a MatchNetwork and then compute an output?

num_features = 3
num_outputs = 1
model = MatchNetwork(n0=num_features, n1=4, n2=num_outputs)

x = ... # Some input example
y = ... # Some matching output label

yhat = model(x) # <-- invokes the forward pass

We can represent the forward pass using math, or more readably with the following graph:

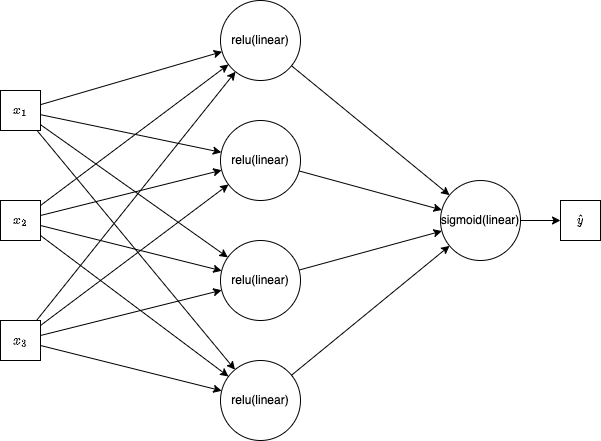
Although the figure above is useful, it is more useful (here) to think about the compute graph. But first, let's see the code needed to create the compute graph. Consider match's implementation of a sigmoid.

# Sigmoid object from nn.py
class Sigmoid(Module):
    """Sigmoid(x) = 1 / (1 + e^(-x))"""

    def forward(self, x: Matrix) -> Matrix:
        # Returns a new Matrix
        return x.sigmoid()

# Sigmoid compute node from matrix.py
def sigmoid(self) -> Matrix:
    """Element-wise sigmoid."""
    result = Matrix(self.data.sigmoid(), children=(self,))

    def _gradient() -> None:
        self.grad += result.data * (1 - result.data) * result.grad

    result._gradient = _gradient
    return result

# Sigmoid math from list2d.py
def sigmoid(self) -> List2D:
    """Return a new List2D object with the sigmoid of each element."""
    vals = [
        [sigmoid(self.vals[i][j]) for j in range(self.ncol)]
        for i in range(self.nrow)
    ]
    return List2D(*self.shape, vals)

The following occurs when sigmoid(x) is called inside our model's forward method:

We call x.sigmoid where x is the output of the previous linear node.
A new Matrix object (called result) is constructed
- Elements in result are computed by taking the sigmoid of each value in the linear output
- The the linear output becomes a child of result in the compute graph
- The new matrix is the same shape as the linear output
A gradient closure (called _gradient) is created with the correct computations for future use
- The closure is attached to the result compute node
- The closure has access to the values and gradient of the linear output
- The closure updates the gradient of the linear node (not itself)

Notice that we cannot compute the gradient of self until we have the gradient of result, which is not computed until its parents are computed. Here's the compute graph:

We now have a compute graph (it includes a reference to loss, which is given below). It was generated by the forward method of MatchNetwork, which was automatically called. Each method call in forward (self.linear1, etc.) builds up the graph. Now that we have the graph, we can compute an optimization function and update all model parameters.

loss = loss_fcn(yhat, y) # Any loss function will do
net.zero_grad()          # Clear previous gradients (no-op first iteration)
loss.backward()          # All gradients are computed

Finally, we just need to update parameter values.

for param in net.parameters():
    # param.grad was computed during the loss.backward() call above
    param.data = param.data - learning_rate * param.grad

See 5.2 Backpropagation for more information.

Adding Functionality

To give you an idea of how to add some new functionality, let's trace through the process I used to add the mean-square-error loss function (MSELoss).

Create a new class inside nn.py: class MSELoss(Module)
- The class must extend the Module class
- Implement the forward method for the new class
  - It can take any arguments that fit your needs
  - It should return a Matrix
  - Most arguments will be a Matrix (matrix in and matrix out, hence "forward")
  - For MSELoss we return ((target - prediction) ** 2).mean()
Add necessary matrix operations to the Matrix class in matrix.py. For MSE, we need
- Subtraction for (target - prediction) (implemented by defining the __sub__ method)
- Exponentiation for _ ** 2 (implemented by defining the __pow__ method)
- Mean for _.mean() (implemented by defining the mean method)
- You might also need to implement operators for the gradient computations (e.g., > for ReLU)
- (note that each of these new methods must build up the compute graph)
Add necessary math to the List2D class in list2d.py. For MSE, we need
- (note that the Matrix class doesn't actually implement any math, just compute graph creation)
- Subtraction is implemented by defining the __sub__ method
- Exponentiation is implemented by defining the __pow__ method
- Mean is implemented by defining the mean method
- (you may need to import new libraries or library functionality)

To recap:

Create a new Module
Add new functionality to Matrix for creating the compute graph
Add new functionality to List2D for computing the matrix math

Testing

The library has a limited number of tests in the file test.py found in the root directory. Unit tests require the PyTorch library. They should be executed with:

# Run this command from the root of the repository (test.py should be in the root)
python -m unittest test

Sandbox

The sandbox directory can be ignored. That is where I am putting ideas for future updates.

anthonyjclark / match

File Structure

Demos

Implementation of Automatic Differentiation

Single "`_`" Convention

Double "`__`" Convention

Compute Graphs

Adding Functionality

Testing

Sandbox

Resources

About

Languages

File Structure

Demos

Implementation of Automatic Differentiation

Single "_" Convention

Double "__" Convention

Compute Graphs

Adding Functionality

Testing

Sandbox

Resources

About

Languages

Single "`_`" Convention

Double "`__`" Convention