Algebraic evaluation is the logic of evaluating noisy agents on unlabeled data. A set of algebraic postulates - universally true for any finite test - can be constructed by connecting the responses of the agents to unknown statistics of their correctness on the test. This treats the evaluation of human or machine agents as an inverse problem where we must go from statistics of their observed agreements and disagreements to inferring their statistics of correctness given those observations.
By construction, these algebraic postulates do not contain any probability theory. Otherwise, they would not be postulates. Any probability theory would require that we specify hyperparameters for it. This immediately raises the possibility of the OOD problem - how do we know the settings of the hyperparameters are valid in the given evaluation context? An algebraic approach side steps the OOD problem by focusing on estimating sample statistics and nothing else.
Since an algebraic approach has no representation of the domain where the noisy algorithms are making their decisions, it can be universal - applicable to all evaluations of noisy algorithms on finite tests. The algebraic postulates, and their associated logic of consistency, discussed here can be summarized by the acronym - NTQR.
- N: the number of classifiers in the group being tested.
- T: the number of tests those classifiers took.
- Q: the number of questions each of those tests contained.
- R: the number of responses that were possible in each of the questions.
The easiest case to consider is the one of evaluating noisy binary classifiers. If we are going to construct postulates for the evaluation of an ensemble of classifiers, we must also confine ourselves to "black-box" methods. Any use of internals related to how the classifiers made their decisions would have the OOD problem of the type of agent involved in the evaluation. For example, methods used to evaluate neural networks could not be used to evaluate a mix of humans and neural networks.
Evaluation is the forgotten twin of learning. AI researchers and their work currently focuses on just one side of the learning process - training. As such, they have missed many of the benefits of considering the theory of evaluation. In particular, the notion that there exists a logic of consistency whenever we are evaluating ensembles of noisy decisions makers on any finite test.
There have been tentative understandings of this logic in the work of some ML researchers. Most notably the agreement equations of Platanios. But the full scope of the mathematics of treating evaluation as a data streaming problem with its own logic is not even understood to exist. This repository means to correct that by providing code and instruction on the mathematics and engineering of using NTQR logic to evaluate noisy human or machine decision makers.
Because it will make us safer. The current theoretical state of AI is one that views all tasks as solvable only by training methods. The 2022 NeurIPS ML Safety Workshop is an exemplar of this exclusive theoretical focus on just one side of learning. Evaluation and its simplicity can help make us safer. Partly because the mathematics of evaluation is simpler than that of training. But also from that common sense point of view we all have about safety - the more ways you have of looking at something, the safer you are.
A safety analogy in another technological realm may clarify why this focus on just one side of the learning problem is needlessly narrow. Consider the humble role of thermometers in cars. Temperature thermometers are not that smart. They just measure and output a single number. But they are useful because they can be hooked to a car's computer and warn us that our engine is overheating.
Where are the evaluation thermometers that can do the same for measuring the quality of the decisions made by noisy judges? What is special about intelligence that would prevent us from doing this? Nothing. Any test taker, whether machine or human, of a finite test with finite responses possible, obeys the same constraints on how their responses can be used to infer their correctness. Grading a test is not an intelligence test. And there is a logic to evaluation on unlabeled data.
The algebraic postulates presented here are universal. There will never be any set of classifiers taking any finite test that violates them.
- Irrespective of how well or badly they did on the test. Irrespective of what domain was used to perform the test.
- Irrespective of what agents where used to carry out the evaluation. That universality is what makes them a logic of evaluation on unlabeled data.
But this logic is not magical. It cannot guarantee that your evaluation will work. GIGO also applies to evaluation on unlabeled data. What makes this logic useful for safety applications is that it can warn you if the ensemble is not good enough to perform a reliable evaluation. This feature alone is what makes it capable of providing a guarantee that no probabilistic or representational approach to evaluation can match.
The simplest and most concrete example of the logic of evaluation on unlabeled data we can consider is binary classification. Central to the problem of evaluation of noisy agents using only their responses is the issue of error correlation. Just like we can create modes of vibration for, say, drumheads. We can do the same for the moments of the statistics of correctness for noisy agents.
The simplest moment of correctness is the marginalized performance of a single agent. In the case of binary classification that would be the two label accuracies for a classifier. The core theorem we will be discussing most in this introduction is the exact solution to the problem of evaluating three error independent binary classifiers. This simple formulation is enough to confront THE fundamental problem in any monitoring of intelligent agents - if they are smarter than us, if we are too lazy to do the work ourselves, if we ourselves do not know the correct answers to the tests we give them, how do we stay safe?
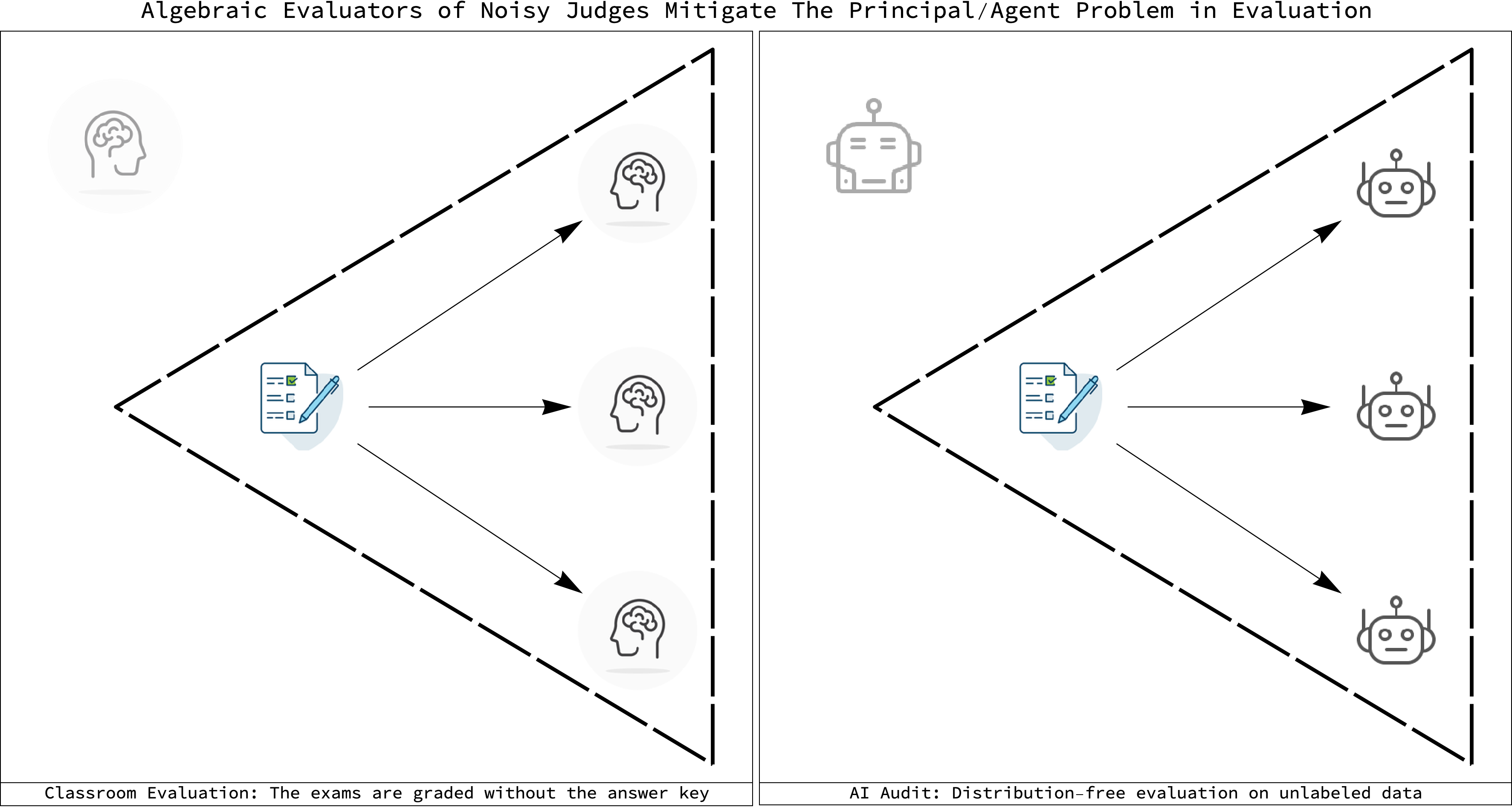
Since this repository will contain code that carries out purely algebraic evaluation of binary classifiers, it cannot be the case that the only way we can evaluate intelligent agents is via the use of ever more intelligent ones.
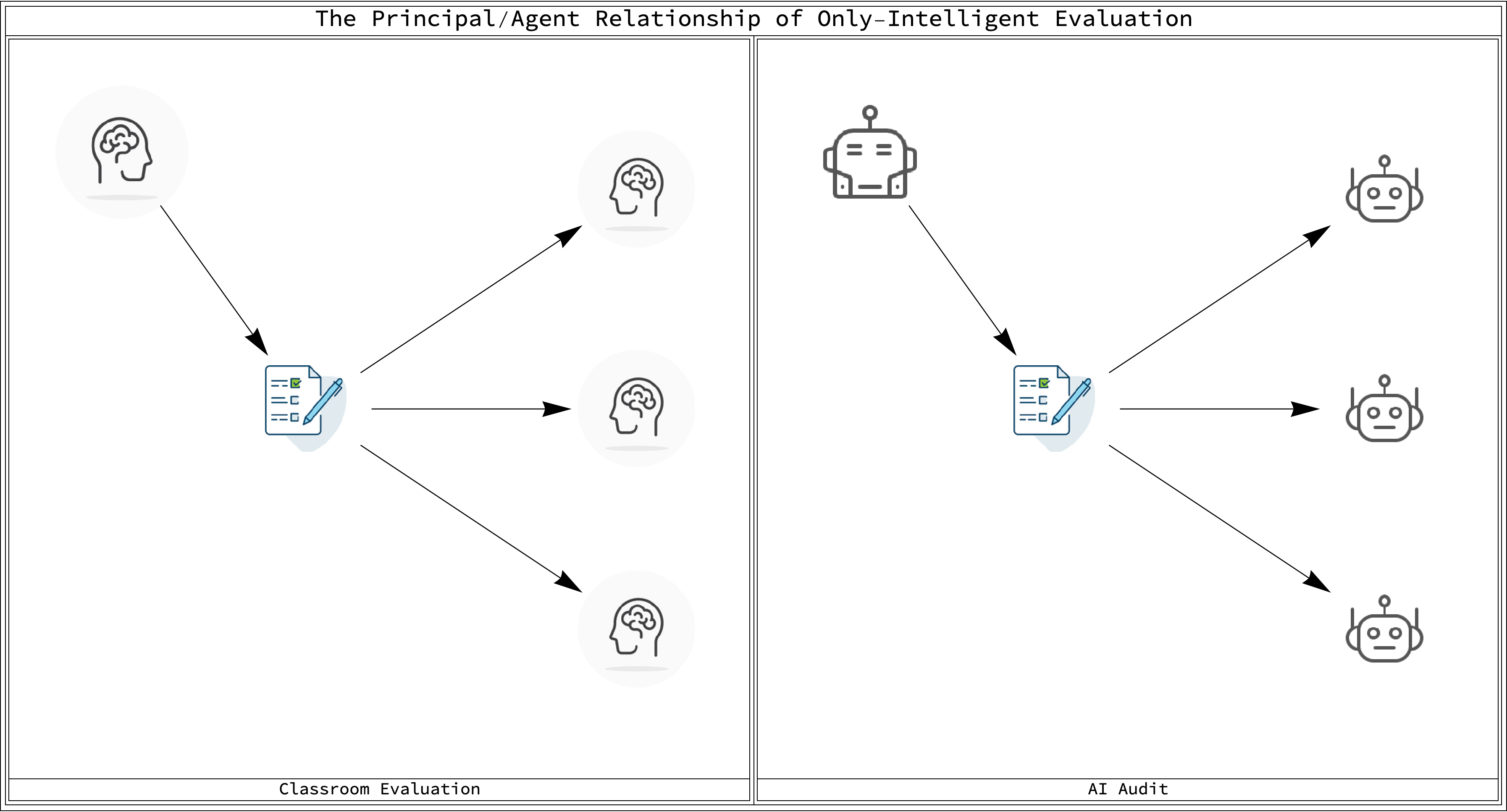
Figure Caption: The fallacy of "only intelligent evaluation"
If only-intelligent evaluation is required, then we truly face a risky AI future. We would be condemmed to a technological arms race with ourselves. Faced with having to monitor AI agents on data that is unlabeled - the hard task of evaluation upon system deployment - we would have to invent succesively smarter AI agents to monitor stupider ones.
This is a pervese race of ''turtles all the way up''. We would be forced to build ever smarter agents that could very well turn malicious or otherwise threaten us. Algebraic evaluation is the way out of this trap we have made for ourselves.
Figure Caption: Bypassing the principal/agent relationship of evaluation to make us safer.
-
AlgebraicEvaluation.py: This Python code contains basic utilities showing how you can turn the counts of voting patterns by binary classifiers into an algebraic formalism for carrying out perfect evaluation of binary classifiers IF they are error independent in the sample. The code details all the sample statistics that are sufficient to write down an exact representation of the algebraic ideal associated with evaluation (the evaluation ideal).
-
EvaluationIdealAndVarietyErrorIndependentTrio.nb: The mathematics of algebraic evaluation is algebraic geometry. Since you are estimating sample statistics, you get to work in a finite dimensional space where all parameters are known. You can build exact polynomial representations of any evaluation you care to set-up for noisy judges on unlabeled data. This notebook shows how to do the simplest algebraic evaluation possible - the tests where the noisy judges where independent in their errors. The almost visceral reactions that critics of algebraic evaluation have to this "spherical cow" in Evaluation Land is telling of the intuition that years of working in Training Land has built up in them. All of them have most likely uttered the phrase "consider an iid sample". In Evaluation Land we get to say "consider noisy judges error independent on the sample". This simplest and purest of algebraic evaluators - combining the decisions from error independent judges - can be used to understand what algebraic evaluation can and cannot do. The mathematics here is that of algebraic geometry. This may seem complex but if you just read the text and enjoy the jumble of algebra, you can get a taste of what can be accomplished by doing evaluation in a purely algebraic manner.
-
TheForgottenRadicalEmpiricismOfRegnault.md: The 19th century French physicist, Henri Victor Regnault, is a forgotten philosopher of science. I would contend a radical empiricist that understood that for evaluation of experts we do not need to be smarter or aware of their mental states. Evaluation is easy, expertise is hard. This essay talks about how Regnault thought about the precision of thermometers. My claim is that whether thermometers or brains, we can evaluate both algebraically. The algebra in this repository details how.
-
SimplestExampleOfEvaluationWithAlgebraicGeometry.md: Becoming familiar with algebraic geometry can be difficult. This essay goes thru the simplest ensemble possible, the trivial ensemble of
$n=1$ . Algebraic geometry may seem like overkill for such a trivial ensemble but we hope the reader will use it as a bridge from their familiarity with evaluating binary classifiers to the unfamiliar topic of the geometry of polynomial ideals.