- 俯角: 水平面から下にある物を見る視線と水平面が成す角
- 仰角: 物を見上げた時の視線と水平面が成す角
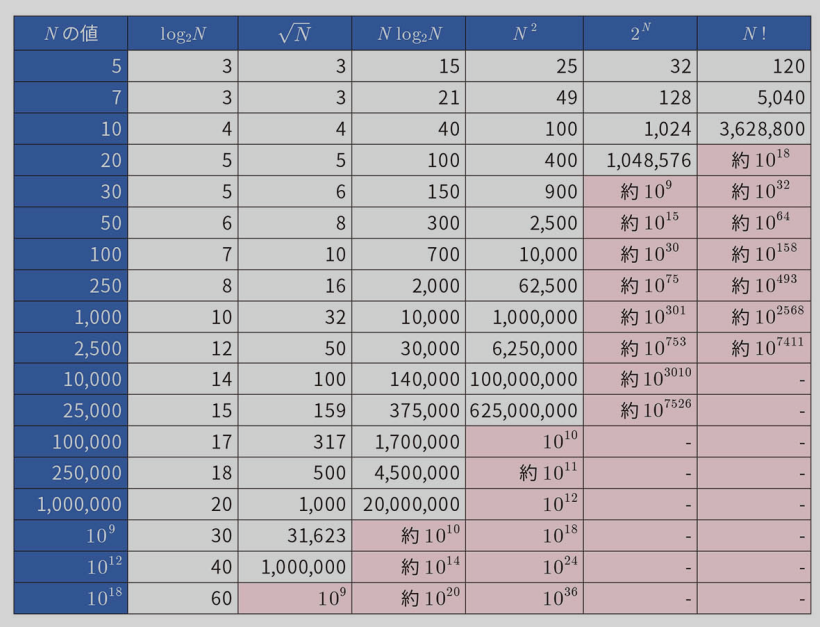
1秒間で処理できる計算ステップ回数は 109 = 1,000,000,000 回程度
- O(log N): いっぱい
- O(N): 10^8
- O(N log N): 10^7
- O(N^2): 10^4
- O(N^3): 300
- O(2^N): 20
- O(N!): 10
指数時間: O(2^N) とか O(N!) とか 多項式時間: O(N^2) とか O(N^3) とか
2^10 -> 1024: だいたい 10^3
指定区間の最小値を得る、みたいなクエリで使える
- 構築に O(N)
- 区間に対するクエリに O(logN)
// 二分木を配列で表現するときは 1-indexed で表現したほうが都合が良い
// 深さと桁数が一致するようになる。 [セグメント木 [いかたこのたこつぼ]](https://ikatakos.com/pot/programming_algorithm/data_structure/segment_tree)
struct SegmentTree {
size: usize,
node: Vec<usize>,
monoid: fn(usize, usize) -> usize,
}
impl SegmentTree {
fn new(n: usize, monoid: fn(usize, usize) -> usize) -> Self {
// ノードの数は 2 の指数倍に正規化する
let mut size = 1;
while size < n {
size *= 2;
}
Self {
size,
// ルートが 1 の完全二分木なので、ノード数は 2n - 1
// node[0] は使わない
node: vec![0; size * 2],
monoid,
}
}
// pos 番目の値を x に更新する
fn update(&mut self, pos: usize, x: usize) {
// 葉のノードの位置
let mut pos = pos + self.size - 1;
self.node[pos] = x;
// 親に上って更新していく
while pos > 0 {
pos /= 2;
self.node[pos] = (self.monoid)(self.node[pos * 2], self.node[pos * 2 + 1]);
}
}
// [l, r) の区間に対するクエリを実行する
fn query(&self, l: usize, r: usize) -> usize {
self._query(l, r, 1, self.size + 1, 1)
}
// [l, r) の区間に対するクエリを実行する
// u は現在見ているノードの位置
// [a, b) は u の担当区間
// u が [l, r) に完全に含まれるまで分解していく
fn _query(&self, l: usize, r: usize, a: usize, b: usize, u: usize) -> usize {
// ありえない区間なら 0 を返す
// MEMO: 0 以外を返したい場合は実装を修正する。例えば、区間の最小値を求める場合は usize::MAX を返す。
if r <= a || b <= l {
return 0;
}
// u の担当区間がクエリ区間に完全に含まれるなら、u の値を返す
if l <= a && b <= r {
return self.node[u];
}
// そうでないなら、左右の子に対して再帰的にクエリを実行する
let m = (a + b) / 2;
let vl = self._query(l, r, a, m, u * 2);
let vr = self._query(l, r, m, b, u * 2 + 1);
// 左右の子の値をマージして返す
(self.monoid)(vl, vr)
}
fn get(&self, pos: usize) -> usize {
self.node[pos + self.size - 1]
}
}遅延評価セグメント木
- 区間加算: O(logN)
- 最小値計算: O(logN)
O(logN)
let v = vec![0, 1, 2, 3, 4, 5, 6];
let i = v.binary_search_by(|&x| {
if x <= 3 {
std::cmp::Ordering::Less
} else {
std::cmp::Ordering::Greater
}
}).unwrap_err();
// i == 4 となるpub trait BinarySearch<T> {
fn lower_bound(&self, key: T) -> usize;
fn upper_bound(&self, key: T) -> usize;
}
impl<T> BinarySearch<T> for [T]
where
T: Ord,
{
fn lower_bound(&self, key: T) -> usize {
let mut ng = -1 as isize;
let mut ok = self.len() as isize;
while ok - ng > 1 {
let mid = (ok + ng) / 2;
if key <= self[mid as usize] {
ok = mid;
} else {
ng = mid;
}
}
ok as usize
}
fn upper_bound(&self, key: T) -> usize {
let mut ng = -1 as isize;
let mut ok = self.len() as isize;
while ok - ng > 1 {
let mid = (ok + ng) / 2;
if key < self[mid as usize] {
ok = mid;
} else {
ng = mid;
}
}
ok as usize
}
}let mut set = BTreeSet::new();
set.insert(1); // O(logN)
set.remove(&1); // O(logN)
// 4以上を探したときの最初の要素を返す
set.range(4..).next();
// 7未満を探したときの最後の要素を返す
set.range(..7).last();たかだか一つしか極値のない関数における極値を探索するアルゴリズム。 つまり、二次関数のような下に凸な関数の最小値を求めることができる。 極値が複数ある場合は使えない。
範囲を 3 分することで、最小値がある範囲を狭めていく。
let mut left = 0.0;
let mut right = 1e9;
for _ in 0..100 {
// 計算の回数を固定して、確実に収束させる
let mid_l = left + (right - left) / 3.0;
let mid_r = right - (right - left) / 3.0;
if f(mid_l) < f(mid_r) {
right = mid_r;
} else {
left = mid_l;
}
}nC2 = n(n-1)/2
- 構築に O(N)
pub struct UnionFind {
parent: Vec<usize>,
rank: Vec<usize>,
size: Vec<usize>,
}
impl UnionFind {
// O(N)
fn new(n: usize) -> Self {
UnionFind {
parent: (0..n).collect(),
rank: vec![0; n],
size: vec![1; n],
}
}
// O(α(N)) ≒ O(1)
fn find(&mut self, x: usize) -> usize {
if self.parent[x] == x {
x
} else {
let p = self.find(self.parent[x]);
self.parent[x] = p;
p
}
}
// O(α(N)) ≒ O(1)
fn unite(&mut self, x: usize, y: usize) {
let x = self.find(x);
let y = self.find(y);
if x == y {
return;
}
if self.rank[x] < self.rank[y] {
self.parent[x] = y;
self.size[y] += self.size[x];
} else {
self.parent[y] = x;
self.size[x] += self.size[y];
if self.rank[x] == self.rank[y] {
self.rank[x] += 1;
}
}
}
// O(α(N)) ≒ O(1)
fn same(&mut self, x: usize, y: usize) -> bool {
self.find(x) == self.find(y)
}
}- 単純な Union-Find は木同士をくっつけるだけ(木が単純に伸びるので最悪 O(N))
- 木をくっつける時に、頂点数が多いグループを上に持っていく単純な工夫で O(logN)になる。
完全 2 分木
- 構築に O(N)
- 要素の追加・削除・更新に最悪でも O(logN)
- 最大値の取得に O(1)
- 要素数の取得に O(1)
- 親ノードは子ノードよりも常に大きい(小さい)という性質を持つ
- 二部グラフの判定
- BFS/DFS で頂点に色を塗っていく
- 隣接する頂点の色が同じ色になる場合は二部グラフではない
- 二部グラフの頂点に辺を一つ追加した時、それは二部グラフのままかどうか
- 別の連結成分に属する頂点に辺を追加する場合、その頂点の色は関係ない
- 同じ連結成分に属する頂点に辺を追加する場合、その頂点の色は異なる必要がある
ダイクストラ法 O(ElogV)
- 重み付き有向グラフの単一始点最短経路問題を解くアルゴリズム
- 単純な DP を使うと O(V^2) で計算
- ヒープを使うと O(ElogV) で計算
- 負の重みを持つエッジがある場合は適用できない -> ベルマンフォード法を使う
- 実装
- 最短距離のみtypical90/src/bin/013.rs
- 最短距離と辿った頂点atcoder_practice/abc252/src/bin/e.rs
- Tips
- 複数の最短経路がある場合、ダイクストラ方を両端からやって、それらの各要素の和が始点と終点の距離になる場合、それは最短経路の一部になる
- dist_from_1[i] + dist_from_n[i] == dist_from_1[n] の時、頂点 i は最短経路の一部
- 複数の最短経路がある場合、ダイクストラ方を両端からやって、それらの各要素の和が始点と終点の距離になる場合、それは最短経路の一部になる
BFS O(E)
- コストが 1 の場合のみ使える
- 実装
01-BFS O(E)
- ※後述 コストが 0 か 1 の場合のみ使える
Floyd-Warshall 法 O(V^3)
- 全頂点間の最短経路を求めるアルゴリズム
- dis[i][j] には i から j への最短経路のコストが入る。初期値は既知のコスト。存在しない経路は inf。
for k in 0..n {
for i in 0..n {
for j in 0..n {
dis[i][j] = std::cmp::min(dis[i][j], dis[i][k] + dis[k][j]);
}
}
}Bellman-Ford 法 O(VE)
let mut dist = vec![std::i64::MAX; n + 1];
dist[1] = 0;
// N-1 回行うと完全に伝搬し、結果が求まる
// もし N 回目の伝搬でdist[i]の値が変わった場合は負の閉路が存在する
for _ in 0..n - 1 {
for &(from, to, cost) in &edges {
let (from, to, cost) = edges[j];
dist[to] = dist[to].min(dist[from] + cost);
}
}- 値が bool の DP は bit DP で高速化できる(典型 90 問 012 の解説動画参照)
- i 行目と i+1 行目の状態を OR すると i+1 行目の状態が得られる
- 64 倍の高速化
- i 行目と i+1 行目の状態を OR すると i+1 行目の状態が得られる
- DP で辿った順序は、DP を埋めたあとに逆順に辿ると得られる
- 最長増加部分列(LIS: Longest Increasing Subsequence)は以下の 2 つを計算すると求められる
dp[i]i 番目まで見た時の LISL[x]長さ x となる LIS の最後の要素の最小値
Strongly Connected Components
- 有向グラフで互いの頂点に到達可能な時、強連結成分という。
- 深さ優先探索を 2 回する
- DFS で帰りがけ順に番号を記録する
- 辺の向きをすべて反転させる
- 1.を逆順にする
- 2.のグラフを 3.の順番に DFS し、到達した頂点を 1 つの強連結成分とする
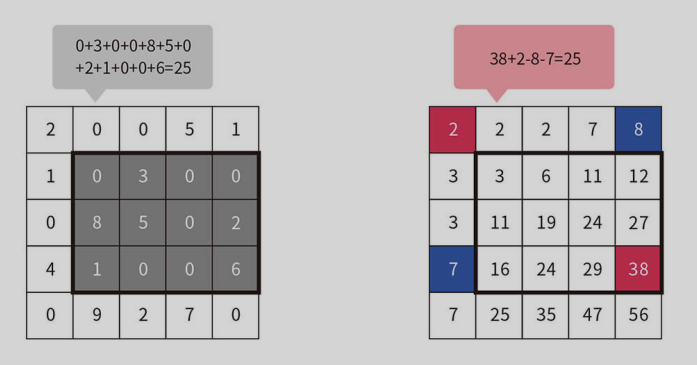
2 次元累積和
// i, j が 1-indexed であることに注意
s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + a[i][j];- 重なり合う区間の数を累積和を使って数える方法
- 2 次元や 3 次元への拡張が容易
- 例えば 2 次元なら O(NHW) かかるところを O(N+HW) で済ませられる
- 始点にプラスの、終点にマイナスの重みをつける
- 各軸の累積和を取る(これによりマイナスの重みをつけた部分は打ち消される)
- 山が 2 つの時は、それぞれの山の石の数を同じ状態で手番が回ってきたら負け。つまり最初から山の数が同じ場合は先手が負け。
- 山が N の場合は、全山の石の数を XOR した値が 0 なら先手負け、0 以外なら先手勝ち。
参考: 組み合わせゲーム理論の基礎と Grundy 数での勝敗判定アルゴリズム | アルゴリズムロジック
Nim のセオリー
- 山ごとに Grundy 数を求める
- それら Grundy 数すべてを XOR する
- 結果が 0 なら負け、0 以外なら勝ち
Grundy 数
- ある状態から遷移可能な状態の Grundy 数の集合の最小の非負整数
- 例えば、ある状態から遷移可能な状態の Grundy 数が {0, 1, 3} なら、その状態の Grundy 数は 2
1≦x のとき、[1,x]までの区間の場合の数は x(x+1)/2 で求められる 例: [1,3] の場合は 3(3+1)/2 = 6 通り (1,2,3,12,13,23)
N-1 箇所の隙間から K-1 個の隙間を選んで仕切りを入れる場合の数は {N-1}C{K-1}
o o o | o | o o o o | o o o N = 11, K = 4 の場合の一例 (10C3 通りある)
AtCoder ABC 132 D - Blue and Red Balls (緑色, 400 点) - けんちょんの競プロ精進記録
DFS で木構造をたどる
Lowest Common Ancestor
- 2 頂点の共通の祖先のうち、最も深いもの
- オイラーツアーを使うと O(N) で求められる
- 2 頂点(A, B)の距離を求められる
- 根から A までの距離 + 根から B までの距離 - 2 x 根から LCA までの距離
|x1 - x2| + |y1 - y2|
以下のように 45 度回転させると
(u, v) = (x + y, x - y)
マンハッタン距離は以下のように表せる(チェビシェフ距離)
max(|u1 - u2|, |v1 - v2|)
証明
|x1 - x2| + |y1 - y2| = max(x1 - x2, x2 - x1) + max(y1 - y2, y2 - y1) とも表すことができるので、この右辺を式変形するとチェビシェフ距離になる。
右回転 x, y = y, -x
左回転 x, y = -y, x
Sliding Window Maximum
- 配列の連続する部分列の最大値を求める
- Deque を使うと O(N) で求められる
- 常に Deque の先頭が最大値になるようにする
- ウィンドウが右に移動する時に以下を行うことで Deque の先頭が常に最大になり、更新が O(1) でできる
- 左端の値を削除
- 右端の値を追加する時に、Deque の末尾から追加しようとしている値より小さな値を削除する
- 2 の倍数: 1 のくらいが 2,4,6,8,0
- 3 の倍数: 各桁の数字の和が 3 の倍数
- 4 の倍数: 下 2 桁が 4 の倍数
- 5 の倍数: 1 のくらいが 0,5
- 8 の倍数: 下 3 桁が 8 の倍数
- 9 の倍数: 各桁の数字の和が 9 の倍数 -> (N mod 9) = (N の各桁の和 mod 9)
- 11 の倍数: 奇数桁目の数字の和 - 偶数桁目の数字の和 が 11 の倍数
- (a + b) mod p = ((a mod p) + (b mod p)) mod p
- 足し算、引き算、掛け算はどのタイミングで mod を取っても答えは変わらない
- 割り算は mod を取る前に逆元を求めてから行う
- 辺の重みが 0 か 1 のグラフの最短経路を求める
- 通常の BFS ではなく、Deque を使う
- 重みが 0 の辺は先頭に、重みが 1 の辺は末尾に追加する
- 重みが 0 の辺は先に探索されるので、最短経路が求まる
n 個の要素を k 個のグループに分ける場合の数
- 例: 4 個の要素の場合、 {4}, {3, 1}, {2, 2}, {2, 1, 1}, {1, 1, 1, 1} の 5 通り
- ベル数の三角形を作ることで求められる
1
1 2
2 3 5
5 7 10 15
上から n 段目、左から k 番目の値は {n - 1}C{k - 1} である
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
fn nck(n: usize) -> Vec<Vec<usize>> {
let mut c = vec![vec![0; n + 1]; n + 1];
c[0][0] = 1;
for i in 1..n {
c[i][0] = 1;
for j in 1..n {
c[i][j] = c[i - 1][j - 1] + c[i - 1][j];
}
}
c
}以下は等価
if ((bit & (1 << i)) != 0) {
// i 番目の bit が立っている
}
if (((bit >> i) & 1) == 1) {
// i 番目の bit が立っている
}- n の約数は、1 から n までの各整数で n を割った時の商が整数になるもの
- 1..=√n まで解を調べて、それぞれの数で N を割ったものも解に含める
let mut ans = vec![];
let mut i = 1;
while i * i <= n {
if n % i == 0 {
ans.push(i);
ans.push(n / i);
}
i += 1;
}n の約数の個数は、n を素因数分解した時の指数の値に 1 を足したもの同士を掛け合わせたものになる 例: 24 = 2^3 x 3^1 なので、約数の個数は (3 + 1) x (1 + 1) = 8
// エラトステネスの篩を利用して n までの各整数の約数の個数を計算
fn divisor_counts(n: usize) -> Vec<usize> {
let mut count = vec![0usize; n + 1];
for i in 1..=n {
let mut j = i;
while j <= n {
count[j] += 1;
j += i;
}
}
count
}- 1 から N までの総和は (N / 2) x (N + 1) で求められる
- たとえば、1 から 50 の場合は 25 x 51 = 1275
- これは、1 + 50 = 51, 2 + 49 = 51, 3 + 48 = 51, ... となるので、25 個の 51 で構成されるため
- a^0 + a^1 + a^2 + ... = 1/(1-a) | 0 < a < 1
- 例えば、a = 0.5 の時、 1 + 0.5 + 0.25 + ... = 2
- 2^0 + 2^1 + 2^2 + ...2^(N-1) = 2^N - 1
// 1からNまでの総和を求める
// 偶数と奇数で処理を分けているのは/2による演算誤差をなくすため
let f = |n: usize| -> usize {
if n % 2 == 0 {
let v1 = (n / 2) % MOD;
let v2 = (n + 1) % MOD;
(v1 * v2) % MOD
} else {
let v1 = ((n + 1) / 2) % MOD;
let v2 = n % MOD;
(v1 * v2) % MOD
}
};全列挙すると TLE になる場合に、二分探索を使える状態にしてから全列挙するとうまく行くことがある。 例えば、A,B,C,D からそれぞれ 1 つずつ選んでその合計がある条件を満たすかを全列挙する場合、A,B と C,D に分けて考えることができる。O(N^3) -> O(N^2 log N)になる。
X を 2 進数表記して 1 のくらいから 0 が何回連続しているか 例: 32(10) = 0010 0000(2) なので、5 回 例: 33(10) = 0010 0001(2) なので、0 回
assert!(32usize.trailing_zeros() == 5);- a ^ a = 0
- a ^ 0 = a
- a ^ b = b ^ a
- a ^ b ^ c = a ^ (b ^ c) = (a ^ b) ^ c
- a ^ b = c ならば a ^ c = b かつ b ^ c = a
- a + b = (a ^ b) + ((a & b) << 1)
B 進法のハッシュ値
B = 100 // 適当に大きな値にする
hash = B^(n-1) x a[0] + B^(n-2) x a[1] + ... + B^0 x a[n-1]
とても大きな数になるので適当な素数 M で mod を取ることが多い -> ハッシュ衝突の可能性
fn digit_sum(mut n: usize) -> usize {
let mut sum = 0;
while n > 0 {
sum += n % 10;
n /= 10;
}
sum
}回文で必要なのは文字列前半の長さ l = (文字列の長さ n + 1) / 2 ※切り上げ 元の文字列の[0,l)と元の文字列の[0, n - l)を反転させたものを結合すると回文になる
let mut s_rev = s[0..n - l].to_vec();
s_rev.reverse();
let mut kaibun = s[0..l].to_vec();
kaibun.extend(s_rev);[2,N]を列挙し、[2,√N]の倍数を除外する 計算量は O(NloglogN)
fn prime_factors(mut n: usize) -> Vec<usize> {
let mut factors = Vec::new();
let mut div = 2;
while div * div <= n {
while (n % div) == 0 {
factors.push(div);
n /= div;
}
div += 1;
}
if n > 1 {
factors.push(n);
}
factors
}- 大きい方の数を「小さい方の数で割った余り」で置き換える
- 片方の数が 0 になったら操作終了、もう片方の数が答え
- 計算量は O(log(a + b))
a と b の最小公倍数は ab / gcd(a, b)
以下の性質を使って a^n を高速に求める a^1 x a^1 = a^2 a^2 x a^2 = a^4 a^4 x a^4 = a^8 ︙
// a^b
fn binpower(a: usize, b: usize) -> usize {
let mut a = a;
let mut b = b;
let mut ans = 1usize;
while b != 0 {
if b % 2 == 1 {
ans = (ans * a) % MOD;
}
a = (a * a) % MOD;
b /= 2;
}
return ans;
}x を a, b いずれかで割り切れるものの個数
=> x/a + x/b - x/ab
X 進数->10 進数
- X 進数 S[0..=4]を 10 進数に直した値は
ans = Σ(S[i] * X^i)
10 進数->X 進数
- 10 進数 N を X 進数に直した値は
S[i] = N % X; N /= Xを繰り返し、最後に S を逆順にする
実装
atcoder_practice/typical90/src/bin/067.rs at main · aliyome/atcoder_practice
fn base_x_to_base10(mut s: Vec<usize>, base: usize) -> Vec<usize> {
let mut x = 1;
let mut ans = 0;
for i in 0..n.len() {
ans += s[i] * x;
x *= base;
}
ans
}
fn base10_to_base_x(n: usize, base: usize) -> usize {
let mut s = vec![];
let mut n = n;
while n > 0 {
s.push(n % base);
n /= base;
}
s.reverse();
s
}- すべての頂点を通る閉路のうち、最短のものを求める問題
- 貪欲法
- 局所探索法
- 2-opt: 2 つの辺を交換することでコストを減らす
// ビット全探索
let mut res = 0;
for bit in 0..1 << n {
let mut a = vec![];
for i in 0..n {
if bit & 1 << i != 0 {
a.push(i);
}
}
if is_ok(a) {
res += 1;
}
}
// DFSで実装する
fn dfs(n: usize, i: usize, a: &mut Vec<usize>) -> usize {
// 終端条件
if i == n {
if is_ok(a) {
return 1;
} else {
return 0;
}
}
// 答えとなる変数
let mut res = 0;
// a に i を追加しない場合
res += dfs(n, i + 1, a);
// a に i を追加する場合
a.push(i);
res += dfs(n, i + 1, a);
// もとに戻す(バックトラック)
a.pop();
res
}// 重複順列 O(NM^N)
// 同じ数を何度使っても良い
// dfs(0, 3, 1, 3, &mut vec![0; 3])
// [1,1,1] [1,1,2] [1,1,3] [1,2,1] ...
// [2,1,1] [2,1,2] [2,1,3] [2,2,1] ...
fn dfs(depth: usize, size: usize, min: usize, max: usize, permutation: &mut Vec<usize>) {
if depth == size {
println!("{:?}", permutation);
return;
}
for i in min..=max {
permutation[depth] = i;
dfs(depth + 1, size, min, max, permutation);
}
}
// 重複組み合わせ O(N*(M+N-1)C(N))
// 同じ数を何度使っても良いが、単調増加になるようにする
// dfs(0, 3, 1, 3, &mut vec![0; 3])
// [1,1,1] [1,1,2] [1,1,3] [1,2,1] [1,2,2] [1,2,3] [1,3,3] [2,2,2] [2,2,3] [2,3,3] [3,3,3]
fn dfs(depth: usize, size: usize, min: usize, max: usize, combination: &mut Vec<usize>) {
if depth == size {
println!("{:?}", combination);
return;
}
for i in min..=max {
combination[depth] = i;
dfs(depth + 1, size, i, max, combination);
}
}
// 組み合わせ O(N*(M)C(N))
// 同じ数を使ってはいけない。単調増加になるようにする。
// dfs(0, 3, 1, 4, &mut vec![0; 3])
// [1,2,3] [1,2,4] [1,3,4] [2,3,4]
fn dfs(depth: usize, size: usize, min: usize, max: usize, combination: &mut Vec<usize>) {
if depth == size {
println!("{:?}", combination);
return;
}
for i in min..=max {
combination[depth] = i;
dfs(depth + 1, size, i + 1, max, combination);
}
}
// 順列 O(N*(M)P(N))
// 同じ数を使ってはいけない。単調増加になるようにする。
// dfs(0, 3, 1, 3, &mut vec![0; 3], &mut vec![false; 4])
// [1,2,3] [1,3,2] [2,1,3] [2,3,1] [3,1,2] [3,2,1]
fn dfs(
depth: usize,
size: usize,
min: usize,
max: usize,
permutation: &mut Vec<usize>,
used: &mut Vec<bool>,
) {
if depth == size {
println!("{:?}", permutation);
return;
}
for i in min..=max {
if !used[i] {
permutation[depth] = i;
used[i] = true;
dfs(depth + 1, size, min, max, permutation, used);
used[i] = false;
}
}
}重み付き有向グラフの 1 つの頂点から別の頂点への最大の流量を求める問題
Ford-Fulkerson 法
- 残余グラフを作る
- 残余グラフで容量が 0 のパスを通らないルートで 1->N のパスを見つける
- そのパスに流せるだけ流す
- 2.に戻る
※残余グラフ
- 残り容量を順方向の辺、使用済み容量を逆方向の辺として追加したグラフ
- 残り容量が 0 の辺は残余グラフには含まない
- 逆方向の辺を辿ると元のグラフの流量を減らす(戻す)ことに対応する
最小カット問題は全く同じアルゴリズムで解けることが知られている。
最小カット問題
重み付き有向グラフの 1 つの頂点から別の頂点へ到達出来る時に、到達できないようにするには最大でどれだけの重みの辺を削除する必要があるかを求める問題
実装
#[derive(Debug, Clone, Default)]
struct Edge {
next: usize,
capacity: usize,
prev: usize,
}
struct MaximumFlow {
size: usize,
used: Vec<bool>,
graph: Vec<Vec<Edge>>,
}
impl MaximumFlow {
fn new(size: usize) -> Self {
Self {
size,
used: vec![false; size],
graph: vec![vec![]; size],
}
}
// 残余グラフの辺を追加
fn add_edge(&mut self, from: usize, to: usize, cap: usize) {
let from_size = self.graph[from].len();
let to_size = self.graph[to].len();
self.graph[from].push(Edge {
next: to,
capacity: cap,
prev: to_size,
});
self.graph[to].push(Edge {
next: from,
capacity: 0,
prev: from_size,
});
}
// 深さ優先探索
fn dfs(&mut self, pos: usize, goal: usize, f: usize) -> usize {
if pos == goal {
return f;
}
self.used[pos] = true;
for i in 0..self.graph[pos].len() {
// 容量 0 の辺は使えない
if self.graph[pos][i].capacity == 0 {
continue;
}
// すでに訪問した頂点にはもう一度行かない
if self.used[self.graph[pos][i].next] {
continue;
}
// 目的地までのパスを探す
let flow = self.dfs(
self.graph[pos][i].next,
goal,
self.graph[pos][i].capacity.min(f),
);
// フローを流せる場合、残余グラフの容量を flow だけ増減させる
if flow >= 1 {
self.graph[pos][i].capacity -= flow;
let next = self.graph[pos][i].next;
let prev = self.graph[pos][i].prev;
self.graph[next][prev].capacity += flow;
return flow;
}
}
// すべての辺を探索しても見つからなかった
0
}
// 頂点 s から頂点 t までの最大フローの総流量
fn max_flow(&mut self, s: usize, t: usize) -> usize {
let mut flow = 0;
loop {
self.used = vec![false; self.size];
let f = self.dfs(s, t, std::usize::MAX);
// フローを流せなくなったら操作終了
if f == 0 {
break;
}
flow += f;
}
flow
}
}- 配列の中で i < j かつ a[i] > a[j] となる組み合わせの数
- バブルソートの交換回数に相当する
- 素朴に実装すると O(N^2)だが、BIT を使うと O(NlogN)で求められる
例
- {1,2,3,4,5}の転倒数は 0
- {1,2,3,5,4}の転倒数は 1 // 5 が 4 より大きいので 1 つ
- {5,1,2,3,4}の転倒数は 4 // 5 が 1,2,3,4 より大きいので 4 つ
https://github.com/aliyome/atcoder_practice/blob/main/tessoku/tessoku-book/src/bin/b57.rs
タプルは Ord を実装していて、各要素の Ord を前から順番に評価する。これで何が嬉しいかと言うと、BinaryHeap にタプルを入れると、最初の要素でソートされることになる。
let mut heap = BinaryHeap::new();
heap.push((Reverse(1), 4));// 配列の連続した重複要素の除去
a.sort();
a.dedup();// BTreeSet
set.iter().next(); // 最小値
set.iter().last(); // 最大値7.count_ones(); // 3 (7 = 111)デカい数の a^b % MOD を計算可能な ModInt 仕組みは a^b は鉄則本 5.3 を参照
const MOD: usize = 1000000007;
use std::ops;
#[derive(Copy, Clone)]
pub struct ModInt {
value: usize,
}
impl ModInt {
pub fn new(value: usize) -> ModInt {
ModInt { value: value % MOD }
}
pub fn value(&self) -> usize {
self.value
}
pub fn inverse(&self) -> ModInt {
// (a, b) -> (x, y) s.t. a * x + b * y = gcd(a, b)
fn extended_gcd(a: isize, b: isize) -> (isize, isize) {
if (a, b) == (1, 0) {
(1, 0)
} else {
let (x, y) = extended_gcd(b, a % b);
(y, x - (a / b) * y)
}
}
let (x, _y) = extended_gcd(self.value() as isize, MOD as isize);
ModInt::new((MOD as isize + x) as usize)
}
// a^n
pub fn pow(&self, mut n: usize) -> ModInt {
let mut res = ModInt::new(1);
let mut x = *self;
while n > 0 {
if n % 2 == 1 {
res *= x;
}
x *= x;
n /= 2;
}
res
}
}
impl ops::Add for ModInt {
type Output = ModInt;
fn add(self, other: Self) -> Self {
ModInt::new(self.value + other.value)
}
}
impl ops::Sub for ModInt {
type Output = ModInt;
fn sub(self, other: Self) -> Self {
ModInt::new(MOD + self.value - other.value)
}
}
impl ops::Mul for ModInt {
type Output = ModInt;
fn mul(self, other: Self) -> Self {
ModInt::new(self.value * other.value)
}
}
impl ops::Div for ModInt {
type Output = ModInt;
fn div(self, other: Self) -> Self {
self * other.inverse()
}
}
impl ops::AddAssign for ModInt {
fn add_assign(&mut self, other: Self) {
*self = *self + other;
}
}
impl ops::SubAssign for ModInt {
fn sub_assign(&mut self, other: Self) {
*self = *self - other;
}
}
impl ops::MulAssign for ModInt {
fn mul_assign(&mut self, other: Self) {
*self = *self * other;
}
}
impl ops::DivAssign for ModInt {
fn div_assign(&mut self, other: Self) {
*self = *self / other;
}
}
// n!
pub fn factorial(n: usize) -> ModInt {
(1..=n).fold(ModInt::new(1), |x, y| x * ModInt::new(y))
}
// nPr (https://ja.wikipedia.org/wiki/%E9%A0%86%E5%88%97#%E9%A0%86%E5%88%97%E3%81%AE%E6%95%B0%E3%81%88%E4%B8%8A%E3%81%92)
pub fn permutation(n: usize, r: usize) -> ModInt {
if n < r {
ModInt::new(0)
} else {
(n - r + 1..=n).fold(ModInt::new(1), |x, y| x * ModInt::new(y))
}
}
// nCr (https://ja.wikipedia.org/wiki/%E7%B5%84%E5%90%88%E3%81%9B_(%E6%95%B0%E5%AD%A6))
pub fn combination(n: usize, r: usize) -> ModInt {
if n < r {
ModInt::new(0)
} else {
permutation(n, r) / factorial(r)
}
}
// nHr (https://ja.wikipedia.org/wiki/%E9%87%8D%E8%A4%87%E7%B5%84%E5%90%88%E3%81%9B#%E9%87%8D%E8%A4%87%E7%B5%84%E5%90%88%E3%81%9B%E3%81%AE%E7%B7%8F%E6%95%B0)
pub fn homogeneous(n: usize, r: usize) -> ModInt {
combination(n + r - 1, r)
}// 数値をアルファベットに変換
print!("{}", (b'a' + p as u8 - 1) as char);インタラクティブ問題
use std::io::{stdin, BufReader};
use proconio::{input, source::line::LineSource};
fn main() {
let stdin = stdin();
let mut source = LineSource::new(BufReader::new(stdin.lock()));
input! {
from &mut source,
n: usize,
};
}