A Member Initiated Meeting at the 2023 Meeting of the Population Association of America (PAA); New Orleans, Apr 12, 2023
- 1. Setup
- 2. Running a simulation and retrieving the input demographic rates
- 3. What can you do with simulation output? Example: estimates of bereavement
- 4. Learn more
- References
Socsim was originally developed for Unix at UC Berkeley (E. Hammel et al. 1976), where it has been maintained for decades. The current release of rsocsim aims to be Operating System-agnostic and, for the most part, back-compatible with the original Socsim distribution. For more on the original SOCSIM, see https://lab.demog.berkeley.edu/socsim/ and especially Mason (2016).
The following description of SOCSIM was adapted from the Supplementary Materials of Alburez‐Gutierrez, Mason, and Zagheni (2021). SOCSIM is an open source and extensible demographic microsimulation program. It is written in the C programming language and relies heavily on arrays of linked lists to keep track of kinship relationships and to store information about simulated individuals. The simulator takes as input initial population files and monthly age-specific fertility and mortality demographic rates. The individual is the unit of analysis of the simulator. Each person is subject to a set of rates, expressed as monthly probabilities of events, given certain demographic characteristics, like age and sex. Every month, each individual faces the risk of experiencing a number of events, including childbirth, death, and marriage. The selection of the event and the waiting time until the event occurs are determined stochastically using a competing risk model. Some other constraints are included in the simulation program in order to draw events only for individuals that are eligible for the events (e.g. to allow for a minimum interval of time between births from the same mother, to avoid social taboos such as incest, etc.). Each event for which the individual is at risk is modeled as a piece-wise exponential distribution. The waiting time until each event occurs is randomly generated according to the associated demographic rates. The individual’s next event is the one with the shortest waiting time.
At the end of the simulation, population files that contain a list of everyone who has ever lived in the population are created. In these files, each individual is an observation in a rectangular data file with records of demographic characteristics for the individual, and identification numbers for key kinship relations. SOCSIM models “closed” populations: Individuals may enter and exit the simulation only by (simulated) birth and death.
SOCSIM has been used extensively in social science research to study, among other things, dynamics of kin availability (E. A. Hammel 2005; Kenneth W. Wachter 1997; Verdery and Margolis 2017), generational overlap (Margolis and Verdery 2019; Alburez‐Gutierrez, Mason, and Zagheni 2021), and kin loss (Zagheni 2011; Verdery et al. 2020; Snyder et al. 2022).
We recommend that you go through point 1 of this tutorial before the start of the workshop. If you have any questions/difficulties, please get in touch with the workshop coordinator (Diego Alburez).
Install the development version of rsocsim from GitHub
(https://github.com/MPIDR/rsocsim). We may have made changes to the
rsocsim package ahead of this workshop. To be on the safe side, if you
had already installed the package, please uninstall it and and install
it again.
# remove.packages("rsocsim")
# install.packages("devtools")
devtools::install_github("MPIDR/rsocsim")Let’s see if everything is working fine. rsocsim has a simple built-in
simulation that you can run to see if the package was installed
correctly. For now, let’s run the code without focusing on the technical
details:
library(rsocsim)
# create a new folder for all the files related to a simulation.
# this will be in your home- or user-directory:
folder = rsocsim::create_simulation_folder()
# create a new supervisory-file. supervisory-files tell socsim what
# to simulate. create_sup_file will create a very basic supervisory file
# and it copies some rate-files that will also be needed into the
# simulation folder:
supfile = rsocsim::create_sup_file(folder)
# Choose a random-number seed:
seed = 300
# Start the simulation:
rsocsim::socsim(folder,supfile,seed)## [1] "Start run1simulationwithfile"
## [1] "C:/Users/calderonbernal/socsim/socsim_sim_8792"
## [1] "300"
## Start socsim
## start socsim main. MAXUYEARS: 200; MAXUMONTHS: 2400
## ratefile: socsim.sup
##
## v18a!-command-line argv[0]: zerothArgument| argv[1]: socsim.sup| argv[2]: 300| argv[3]: 1
## random_number seed: 300| command-line argv[1]: socsim.sup| argv[2]: 300
## compatibility_mode: 1| command-line argv[3]: 1
## Socsim Version: STANDARD-UNENHANCED-VERSION
## initialize_segment_vars
## initialize_segment_vars done
## 18b - loading -.sup-file: socsim.sup
## 18b-load.cpp->load . socsim.sup
## #load.cpp->load 4. socsim.sup
## 18b-load.cpp->load . SWEfert2022
## #load.cpp->load 4. SWEfert2022
## Incomplete rate set, will add rate till MAXUYEARS (death-->1.0; others:0.0) 12
## Incomplete rate set, will add rate till MAXUYEARS (death-->1.0; others:0.0) 12
## 18b-load.cpp->load . SWEmort2022
## #load.cpp->load 4. SWEmort2022
## Incomplete rate set, will add rate till MAXUYEARS (death-->1.0; others:0.0) 12
## Incomplete rate set, will add rate till MAXUYEARS (death-->1.0; others:0.0) 12
## Incomplete rate set, will add rate till MAXUYEARS (death-->1.0; others:0.0) 12
## Incomplete rate set, will add rate till MAXUYEARS (death-->1.0; others:0.0) 12
## Incomplete rate set, will add rate till MAXUYEARS (death-->1.0; others:0.0) 12
## Incomplete rate set, will add rate till MAXUYEARS (death-->1.0; others:0.0) 12
## Incomplete rate set, will add rate till MAXUYEARS (death-->1.0; others:0.0) 12
## Incomplete rate set, will add rate till MAXUYEARS (death-->1.0; others:0.0) 12
## ------------4marriage_eval == DISTRIBUTION . socsim.sup
## ------------6------------7
## output file names:
## init_new.opop|init_new.omar|init_new.opox|sim_results_socsim.sup_300_/result.pyr|sim_results_socsim.sup_300_/result.stat|init_new.otx|
## fix pop pointers..
## Starting month is 601
## Initial size of pop 8000 (living: 8000)
## ------------aa3s------------aa32New events generated for all living persons
## ------------b1month: 700 PopLive: 9414 Brths: 16 Dths: 0 Mrgs: 11 Dvs: 0 Mq: 3728 Fq:0 ti1: 0.3 ti2: 0.007000 0.5037
## month: 800 PopLive: 10926 Brths: 12 Dths: 1 Mrgs: 6 Dvs: 0 Mq: 3890 Fq:0 ti1: 0.4 ti2: 0.008000 0.5287
## month: 900 PopLive: 12260 Brths: 14 Dths: 0 Mrgs: 4 Dvs: 0 Mq: 4031 Fq:0 ti1: 0.6 ti2: 0.006000 0.3693
## month: 1000 PopLive: 13397 Brths: 9 Dths: 2 Mrgs: 4 Dvs: 0 Mq: 4134 Fq:0 ti1: 0.7 ti2: 0.006000 0.3511
## month: 1100 PopLive: 14172 Brths: 16 Dths: 6 Mrgs: 6 Dvs: 0 Mq: 4135 Fq:0 ti1: 0.9 ti2: 0.008000 0.4679
## month: 1200 PopLive: 14518 Brths: 13 Dths: 11 Mrgs: 6 Dvs: 0 Mq: 4000 Fq:0 ti1: 1.0 ti2: 0.006000 0.3750
## month: 1300 PopLive: 14323 Brths: 14 Dths: 20 Mrgs: 4 Dvs: 0 Mq: 3891 Fq:0 ti1: 1.2 ti2: 0.008000 0.5284
## month: 1400 PopLive: 13816 Brths: 13 Dths: 15 Mrgs: 4 Dvs: 0 Mq: 3746 Fq:0 ti1: 1.4 ti2: 0.008000 0.5701
## month: 1500 PopLive: 13330 Brths: 11 Dths: 11 Mrgs: 5 Dvs: 0 Mq: 3679 Fq:0 ti1: 1.6 ti2: 0.009000 0.6649
## month: 1600 PopLive: 12944 Brths: 10 Dths: 15 Mrgs: 4 Dvs: 0 Mq: 3593 Fq:0 ti1: 1.7 ti2: 0.008000 0.6197
## month: 1700 PopLive: 12525 Brths: 10 Dths: 20 Mrgs: 5 Dvs: 0 Mq: 3436 Fq:0 ti1: 1.9 ti2: 0.007000 0.5929
## month: 1800 PopLive: 12009 Brths: 10 Dths: 16 Mrgs: 7 Dvs: 0 Mq: 3275 Fq:0 ti1: 2.0 ti2: 0.008000 0.7459
##
##
## Socsim Main Done
## Socsim Done.
## [1] "restore previous working dir: U:/SOCSIM/rsocsim_workshop_paa"
## [1] 1
You should see a long output in the console, at the end of which is the message “Socsim done”. Ignore the two warning messages (‘can’t open transition history file. Hope that’s OK’). They are expected.
For more details on the package, the SOCSIM simulator, its history and
applications, see rsocsim’s website:
https://mpidr.github.io/rsocsim/.
We will need these other for this workshop (if you don’t have them already, please install them):
# devtools::install_github("MPIDR/rsocsim")
library(rsocsim)
# install.packages("tidyverse")
library(tidyverse) #For data wrangling
# install.packages("ggh4x")
library(ggh4x) #for extended facet plotting
# install.packages("data.table") #for large datasets
library(data.table)Instructor: Liliana P. Calderón-Bernal, https://twitter.com/lp_calderonb
- Use data from the Human Fertility Database (HFD) and Human Mortality Database (HMD) to create a simulation from scratch
- Run a simple SOCSIM simulation for the USA
- Estimate age-specific fertility and mortality rates using the SOCSIM-generated microdata
- Check that the ‘output’ SOCSIM rates match the ‘input’ HFD/HMD rates
To provide an example of rsocsim usage, we will run a SOCSIM
microsimulation for the United States of America (USA) over the period
1933-2020. This microsimulation uses as input: age-specific fertility
rates by calendar year and year of age downloaded from the Human
Fertility Database (HFD), and
age-specific probabilities of death by sex downloaded from the Human
Mortality Database (HMD). To run the
simulation, the original HFD and
HMD data must be first converted to
monthly rates/probabilities and SOCSIM format as described in Socsim
Oversimplified (c.f. Mason 2016 for details). The rates corresponding to
each year are specified in the supervisory file socsim_USA.sup,
provided in this repository, which will be used to run the simulation.
The first segment of the simulation runs for 100 years (1200 months) to
produce a stable age structure, based on HFD rates and HMD probabilities
for 1933. Each of the following segments runs for one year (12 months)
with the corresponding fertility and mortality files.
The structure of the rate files is essential to run SOCSIM. According to Socsim Oversimplified (c.f. Mason 2016, 26–28), a rate block is a complete set of age specific rates governing a demographic event for people of a particular sex, group and marital status. In the rate files, the order is always event (birth, death, marriage), group (1, ..), sex (F or M), and marital status (married, single, divorced, widowed). For the birth rates, this can be followed by number indicating parity. Each subsequent line contains a one month rate or probability and the age interval over which it holds (years and months of the upper age bound). The interval includes the upper age bound in previous line and ends just before the upper age bound in current line. The first two numbers are years and months of the upper age bound, which are added together, e.g. upper age bound of “1 0” or “0 12” refers to the first year of life [0,1).
Let’s load some functions we prepared to write SOCSIM rate files from HFD and HMD.
# Load functions to write SOCSIM rate files
source("functions.R")For the input Age-Specific Female Fertility Rates, we keep the whole age range included in HFD [12-55], but limit the open-ended age intervals 12- and 55+ to one year, i.e. [12-13) and [55-56). Additionally, SOCSIM requires a final age category with an upper bound corresponding to the maximum length of life, that we fixed to [56-110], to be consistent with HMD data.
To convert the HFD annual fertility rates to ‘SOCSIM’ monthly fertility rates, we assume that they are constant over the year and divide them by 12 months. The are identical for all marital status, but are specified for single and married women in the rate files. Other marital status (divorced, widowed, cohabiting) follow SOCSIM’s rate default rules.
For this exercise, we will use Period Age-specific fertility rates all
birth orders combined, by calendar year and age for the desired country
(saved in Input/asfrRR.txt), downloaded from the HFD
website.
The function below converts HFD data to SOCSIM format following the procedure explained above. To run it, type the name of the country as used in HFD (here, “USA”).
write_socsim_rates_HFD(Country = "USA") For the input Age-Specific Probabilities of Death, we keep the whole age
range included in HMD [0-110+] but limit the open-ended age interval
110+ to one year, i.e. [110-111). Originally, SOCSIM had an upper bound
of 100 years, but in rsocsim the maximum age has been extended to 200
years.
We use the probabilities of death (qx) by sex from from HMD period life tables, that had been already smoothed for ages 80 and older, at which observed death rates M(x) display considerable random variation (For details, see the HMD Methods Protocol Wilmoth et al. 2021, 34–36).
To convert the annual HMD probabilities to monthly ‘SOCSIM’
probabilities, we assume that the probability of dying is constant over
the year and use the formula
proposed by Kenneth Watcher (Kenneth W. Wachter 2014, 53). For the
open-ended age interval 110+, monthly probabilities are equal to 1/12.
The probabilities of death are identical for all marital status of each
sex, and are only specified for single women and single men in the rate
files. Other marital status will follow SOCSIM’s rate default rules.
To write the input mortality files, please use the file
Input/ltfper_1x1.txt (period life tables 1x1, Age interval × Year
interval, for females and males for the U.S.A) downloaded from the HMD
website.
The function below converts HMD data to SOCSIM format following the procedure explained above. To run it, type the name of the country as used in HMD (here, “USA”).
write_socsim_rates_HMD(Country = "USA")Now that we have the rate files, let’s create the initial population (.opop) and marriage (.opop) files. The initial .opop will have a size of 20000, with randomly assigned sex and dates of birth, and group 1 for all. Other columns will be completed during the simulation. The initial .omar will be an empty file.
# Set size of initial population
size_opop <- 20000
# Create data.frame with 14 columns and nrows = size_opop
presim.opop <- setNames(data.frame(matrix(data = 0, ncol = 14, nrow = size_opop)),
c("pid","fem","group","nev","dob","mom","pop",
"nesibm","nesibp","lborn","marid","mstat","dod","fmult"))
# Add pid 1:sizeopop
presim.opop$pid <- 1:size_opop
# Add sex randomly
presim.opop$fem <- sample(0:1, nrow(presim.opop), replace = T)
# Add group 1 for all individuals
presim.opop$group <- 1
# Add random dates of birth (max age around 50)
presim.opop$dob <- sample(600:1200, nrow(presim.opop), replace = T)
# Write initial population for pre-simulation (without fertility multiplier)
write.table(presim.opop, "presim.opop", row.names = F, col.names = F)
## Create an empty data frame for presim.omar
presim.omar <- data.frame()
# Write empty omar for pre-simulation
write.table(presim.omar, "presim.omar", row.names = F, col.names = F)Now that we have created the input rate files and the initial population
and marriage files, we can run the simulation. To use the socsim
function, we need to specify the folder where the supervisory and the
rate files are, the name of the supervisory file for the rates retrieved
from HFD and HMD (1933-2020), and a seed number for the simulation.
# Specify the folder where the supervisory and the rate files are.
# If the R session is running through the project, you can use the following command.
folder <- getwd()
# Type the name of the supervisory file stored in the above folder:
supfile <- "socsim_USA.sup"
# Choose a seed number (today's date) for the simulation:
seed <- "120423"
# Run a single SOCSIM-simulation with a given folder and the provided supervisory file
# using the "future" process method
rsocsim::socsim(folder, supfile, seed, process_method = "future")The simulation results are ready. We can use the read_opop and
read_omar functions from the rsocsim package to import the output
population and marriage files into R.
## Read the opop file using the read_opop function
opop <- rsocsim::read_opop(folder = getwd(), supfile = "socsim_USA.sup",
seed = "120423", suffix = "", fn = NULL)## [1] "read population file: U:/SOCSIM/rsocsim_workshop_paa/sim_results_socsim_USA.sup_120423_/result.opop"
## Read the omar file using the read_opop function
omar <- rsocsim::read_omar(folder = getwd(), supfile = "socsim_USA.sup",
seed = "120423", suffix = "", fn = NULL)## [1] "read marriage file: U:/SOCSIM/rsocsim_workshop_paa/sim_results_socsim_USA.sup_120423_/result.omar"
Let’s have a glimpse on the simulated population and marriage files.
The population file (.opop) contains one record for each individual who was ever alive during the simulation. Each record (row) provides the following information for a given individual: person id (pid), sex (fem, 1 for female and 0 for male), group identifier (group), next scheduled event (nev), date of birth (dob), person id of mother (mom), person id of father (pop), person id of next eldest sibling through mother (nesibm), person id of next eldest sibling through father (nesibp), person id of last born child (lborn), id of most recent marriage in .omar file (marid), marital status at end of simulation (mstat), date of death (dod, or 0 if alive at end of simulation) and fertility multiplier (fmult). For more information on what these columns are, see: https://lab.demog.berkeley.edu/socsim/CurrentDocs/socsimOversimplified.pdf.
head(opop)## pid fem group nev dob mom pop nesibm nesibp lborn marid mstat dod fmult
## 1 1 1 1 65 699 0 0 0 0 0 0 1 1502 0.172002
## 2 2 0 1 65 1070 0 0 0 0 0 0 1 1880 0.000000
## 3 3 1 1 65 857 0 0 0 0 23335 2414 3 1715 0.605228
## 4 4 0 1 65 859 0 0 0 0 23000 2233 4 1752 0.000000
## 5 5 1 1 65 1152 0 0 0 0 23947 2705 4 1820 0.701332
## 6 6 0 1 65 1069 0 0 0 0 28769 4770 3 2135 0.000000
The marriage file (.omar) contains one record for each marriage. Each marriage record provides the following information: marriage id number (mid), wife’s person id (wpid), husband’s person id (hpid), date marriage began (dstart), date marriage ended (dend, it’s 0 if in force at the end of simulation), reason marriage ended (rend), marriage id of wife’s next most recent prior marriage (wprior), marriage id of husband’s next most recent prior marriage (hprior).
head(omar)## mid wpid hpid dstart dend rend wprior hprior
## 1 1 4254 14055 1201 1535 3 0 0
## 2 2 12169 2424 1201 1680 3 0 0
## 3 3 19824 14932 1201 1565 3 0 0
## 4 4 6919 5970 1201 1514 3 0 0
## 5 5 12475 11182 1201 1609 3 0 0
## 6 6 1628 12760 1201 1700 3 0 0
To check the accuracy of our microsimulation for the USA, we can
estimate and compare input and output age-specific fertility and
mortality rates (ASFR and ASMR) by sex. For this purpose, we can use the
estimate_fertility_rates and estimate_mortality_rates functions from
the package. Please note that these calculate age-specific rates for
both fertility and mortality, as they use mid-year population size by
sex and age as an estimate of person-years lived during the year. Hence,
the population in the denominator includes all those who were born
before the
of
July of a given year and die in or after July of that year or are still
alive at the end of the simulation. Due to the limited population size
in a microsimulation (especially, of survivors at old ages), sometimes
few or no individuals of a specific age are alive at a exact point in
time (here, 1st July). Hence, it is possible to obtain rates higher than
1, equal to 0 (0 Events/Population), infinite (Events/0 Population) and
NaN (0 Events/0 Population) values with these functions.
To run them, we need to define some arguments: the .opop file opop,
final year of the simulation final_sim_year, the minimum and maximum
years for which we want to estimate the rates, [year_min and
year_max), the size of the year group year_group, the minimum and
maximum age for fertility [age_min_fert and age_max_fert) or the
maximum age for mortality age_max_mort) and the size of the age group
age_group. We can compute the rates by different year and age groups
(e.g., 1, 5, or 10), but please check that the minimum and maximum years
and ages correspond to the groups size. Let’s run the code.
# Estimate age-specific fertility rates
asfr_sim <- rsocsim::estimate_fertility_rates(opop = opop,
final_sim_year = 2020, #[Jan-Dec]
year_min = 1935, # Closed [
year_max = 2020, # Open )
year_group = 5,
age_min_fert = 10, # Closed [
age_max_fert = 55, # Open )
age_group = 5) #[,)
# Estimate age-specific mortality rates
asmr_sim <- rsocsim::estimate_mortality_rates(opop = opop,
final_sim_year = 2020, # [Jan-Dec]
year_min = 1935, # Closed
year_max = 2020, # Open )
year_group = 5,
age_max_mort = 110, # Open )
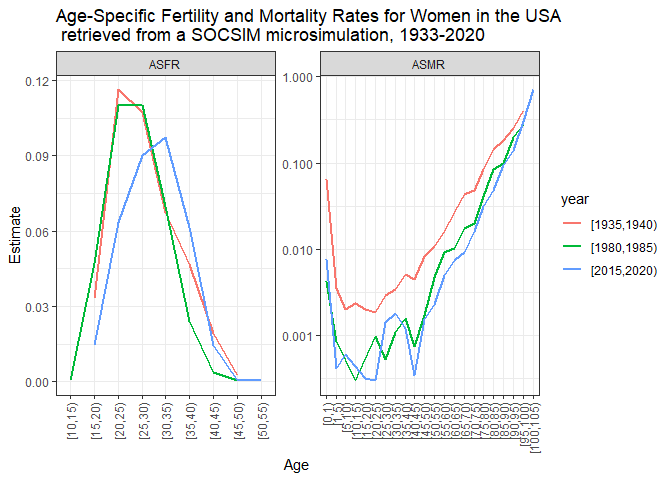
age_group = 5) #[,)We can now plot our SOCSIM-derived estimates of ASFR and ASMR for women in some selected years.
# Choose years to plot (in intervals).
yrs_plot <- c("[1935,1940)", "[1980,1985)", "[2015,2020)")
# Get the age levels to define them before plotting and avoid wrong order
age_levels <- levels(asmr_sim$age)
bind_rows(asfr_sim %>%
mutate(rate = "ASFR",
sex = "female"),
asmr_sim %>%
mutate(rate = "ASMR") %>%
filter(sex == "female")) %>%
mutate(age = factor(as.character(age), levels = age_levels)) %>%
# Filter rates of 0, infinite (N_Deaths/0_Pop) and NaN (0_Deaths/0_Pop) values
filter(socsim !=0 & !is.infinite(socsim) & !is.nan(socsim)) %>%
filter(year %in% yrs_plot) %>%
ggplot(aes(x = age, y = socsim, group = year, colour = year)) +
geom_line(linewidth = 1) +
facet_wrap(. ~ rate, scales = "free") +
facetted_pos_scales(y = list(ASFR = scale_y_continuous(),
ASMR = scale_y_continuous(trans = "log10"))) +
theme_bw() +
scale_x_discrete(guide = guide_axis(angle = 90)) +
labs(title = "Age-Specific Fertility and Mortality Rates for Women in the USA \n retrieved from a SOCSIM microsimulation, 1933-2020",
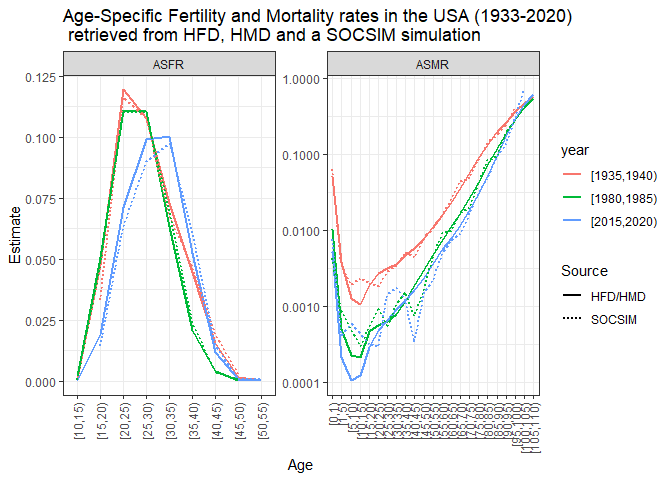
x = "Age", y = "Estimate")As an additional check, we can compare the age-specific fertility and mortality rates retrieved from the SOCSIM output with the original HFD and HMD data used as input for our microsimulation. Since our estimates of fertility and mortality rates from SOCSIM output are grouped by 5-year age groups and 5-year calendar periods in the previous example, we should first estimate the aggregated measures (5x5) from the original HFD and HMD data. For plotting the data together, we also need some data wrangling.
Let’s start with fertility estimates.
# Extract year and age breaks used in the estimate_fertility_rates() to apply the same values to HFD data
# Year breaks. Extract all the unique numbers from the intervals.
year_breaks_fert <- unique(as.numeric(str_extract_all(asfr_sim$year, "\\d+", simplify = T)))
# Year range to filter HFD data
year_range_fert <- min(year_breaks_fert):max(year_breaks_fert-1)
# Age breaks of fertility rates. Extract all the unique numbers from the intervals
age_breaks_fert <- unique(as.numeric(str_extract_all(asfr_sim$age, "\\d+", simplify = T)))
# Read the same HFD file used to write the input fertility files
HFD <- read.table(file = "Input/USAasfrRR.txt",
as.is=T, header=T, skip=2, stringsAsFactors=F)
# Wrangle data and compute monthly fertility rates
HFD <- HFD %>%
mutate(Age = case_when(Age == "12-" ~ "12",
Age == "55+" ~ "55",
TRUE ~ Age),
Age = as.numeric(Age)) %>%
filter(Year %in% year_range_fert) %>%
mutate(year = cut(Year, breaks = year_breaks_fert,
include.lowest = F, right = F, ordered_results = T),
age = cut(Age, breaks = age_breaks_fert,
include.lowest = F, right = F, ordered_results = T)) %>%
filter(!is.na(age)) %>%
group_by(year, age) %>%
summarise(ASFR = mean(ASFR)) %>%
ungroup() %>%
mutate(Source = "HFD/HMD",
Rate = "ASFR")
# Wrangle SOCSIM data
SocsimF <- asfr_sim %>%
rename(ASFR = socsim) %>%
mutate(Source = "SOCSIM",
Rate = "ASFR")Then, the mortality estimates. Here, we compare the SOCSIM mid-year ASMR with central death rates from HMD life tables.
# Extract year and age breaks used in the estimate_mortality_rates() to apply the same values to HMD data
# Year breaks. Extract all the unique numbers from the intervals
year_breaks_mort <- unique(as.numeric(str_extract_all(asmr_sim$year, "\\d+", simplify = T)))
# Year range to filter HMD data
year_range_mort <- min(year_breaks_mort):max(year_breaks_mort-1)
# Age breaks of mortality rates. Extract all the unique numbers from the intervals
age_breaks_mort <- unique(as.numeric(str_extract_all(asmr_sim$age, "\\d+", simplify = T)))
# Read the same HMD female life table 1x1 file used to write the input mortality files
ltf <- read.table(file="Input/fltper_1x1.txt",
as.is=T, header=T, skip=2, stringsAsFactors=F)
# Read the same HMD male life table 1x1 file used to write the input mortality files
ltm <- read.table(file="Input/mltper_1x1.txt",
as.is=T, header=T, skip=2, stringsAsFactors=F)
# Wrangle HMD life tables
HMD <- ltf %>%
select(Year, Age, mx) %>%
mutate(Sex = "Female") %>%
bind_rows(ltm %>%
select(Year, Age, mx) %>%
mutate(Sex = "Male")) %>%
mutate(Age = ifelse(Age == "110+", "110", Age),
Age = as.numeric(Age)) %>%
filter(Year %in% year_range_mort) %>%
mutate(year = cut(Year, breaks = year_breaks_mort,
include.lowest = F, right = F, ordered_results = T),
age = cut(Age, breaks = age_breaks_mort,
include.lowest = F, right = F, ordered_results = T)) %>%
filter(!is.na(age)) %>%
group_by(year, Sex, age) %>%
summarise(mx = mean(mx)) %>%
ungroup() %>%
mutate(Source = "HFD/HMD",
Rate = "ASMR")
# Wrangle SOCSIM data
SocsimM <- asmr_sim %>%
rename(mx = socsim) %>%
mutate(Sex = ifelse(sex == "male", "Male", "Female"),
Source = "SOCSIM",
Rate = "ASMR") %>%
select(year, Sex, age, mx, Source, Rate)Finally, we can plot together the age-specific fertility and mortality rates (ASFR and ASMR) from SOCSIM vs HFD and HMD for women in the USA.
## Plotting ASFR and ASMR (for females) from HFD/HMD vs SOCSIM
bind_rows(HFD %>% rename(Estimate = ASFR),
SocsimF %>% rename(Estimate = ASFR)) %>%
mutate(Sex = "Female") %>%
bind_rows(HMD %>% rename(Estimate = mx),
SocsimM %>% rename(Estimate = mx)) %>%
# Filter rates of 0, infinite (N_Deaths/0_Pop) and NaN (0_Deaths/0_Pop) values
filter(Estimate != 0 & !is.infinite(Estimate) & !is.nan(Estimate)) %>%
filter(Sex == "Female") %>%
mutate(age = factor(as.character(age), levels = age_levels)) %>%
filter(year %in% yrs_plot) %>%
ggplot(aes(x = age, y = Estimate, group = interaction(year, Source)))+
facet_wrap(. ~ Rate, scales = "free") +
geom_line(aes(colour = year, linetype = Source), linewidth = 1)+
scale_linetype_manual(values = c("HFD/HMD" = "solid","SOCSIM" = "11")) +
facetted_pos_scales(y = list(ASFR = scale_y_continuous(),
ASMR = scale_y_continuous(trans = "log10")))+
scale_x_discrete(guide = guide_axis(angle = 90)) +
labs(title = "Age-Specific Fertility and Mortality rates in the USA (1933-2020) \n retrieved from HFD, HMD and a SOCSIM simulation",
x = "Age") +
theme_bw()Instructor: Mallika Snyder, https://twitter.com/mallika_snyder
- Learn how to analyze SOCSIM output
- Understand how SOCSIM records kin ties
- Use SOCSIM output from the previous section to describe levels of family bereavement in the USA
After running our simulation code, SOCSIM provides us with a synthetic genealogy for the entire population. We know when people are born, when they die, when they marry, and who their parents and spouse are. What can we do with this information?
One advantage of using a tool like SOCSIM is that we can identify
extended kin networks, especially for more distant kin that would be
hard to link together using a census or a household survey. For example,
how straightforward would it be to find an individual’s
great-grandmother in a household survey, assuming odds of co-residence
are not high? Of course, some kinds of kin are easier to identify than
others, based on the information we have in SOCSIM (and some may be
impossible to find). When identifying kin, we use lateral kin
relationships—such as parents and children–or affinal kin
relationships—such as spouses. This is the principle behind the
retrieve_kin function included in this package, which can be used to
identify kin from a variety of kin relationships (parents, grandparents,
spouses, children, and much more). You can read the full documentation
for this function by typing ?retrieve_kin into your RStudio console.
An important note is that the kinship terms used in this function are
currently North America-specific: other regions may have very different
kinship systems, which may influence kin availability.
In addition to enabling us to more easily identify networks, SOCSIM also provides us with valuable information about the timing of vital events, like births, deaths, and marriages, in these networks. This can help us connect changes in the vital rates that go into SOCSIM to changes in the networks that our simulated people have available to them, often at a very fine temporal level (months or years). In this workshop, we will focus on just one example–kin loss–but there are many more possible ways to use SOCSIM to study these and other questions about kinship dynamics.
In previous research, SOCSIM has been especially helpful for studying kin loss in connection with mortality change (Zagheni 2011; Verdery et al. 2020; Snyder et al. 2022). Here we will focus on a simple example, changes in the rate of experiencing the loss of a relative over time. We will define as our reference group women aged 25-39 and alive in a given year: thus, the sample frame will change in each year. Note that the denominator is all women, not just those with a relative alive.
In our code, we will approach this by writing a function that we will loop over each year of interest. The function will take in a year, look for the individuals of the relevant age who are alive that year, identify the years of death of their kin, and then calculate the proportion of our sample who experienced a loss. For further intuition, we will also calculate the share of women who had a relative alive in the previous year. The code is a simplified version of functions used in a previous research paper (Snyder et al. 2022).
The first thing we require is a helper function to identify the year of interest.
#We won't discuss how this function works, but it uses the final simulation year (January-December)
#and the last simulated month to convert our monthly dates into yearly ones
asYr <- function(month, last_month=last_month, final_sim_year=final_sim_year) {
return(final_sim_year - trunc((last_month - month)/12))
}Now we can load the data and define a few relevant parameters.
## Read the opop file using the read_opop function
opop <- rsocsim::read_opop(folder = getwd(), supfile = "socsim_USA.sup",
seed = "120423", suffix = "", fn = NULL)## [1] "read population file: U:/SOCSIM/rsocsim_workshop_paa/sim_results_socsim_USA.sup_120423_/result.opop"
## Read the omar file using the read_opop function
omar <- rsocsim::read_omar(folder = getwd(), supfile = "socsim_USA.sup",
seed = "120423", suffix = "", fn = NULL)## [1] "read marriage file: U:/SOCSIM/rsocsim_workshop_paa/sim_results_socsim_USA.sup_120423_/result.omar"
#Parameters specific to this simulation: will need to be changed
last_month <- max(opop$dob) # Last simulated month
final_sim_year <- 2020#Cleaning our population file
opop <- opop %>%
#Fixing dates of death for individuals still living at the end
mutate(dod = if_else(dod == 0, last_month, dod)) %>%
#Dates of birth and death in years for both individual and parents
mutate(dob_year = asYr(dob, last_month=last_month, final_sim_year=final_sim_year),
dod_year = asYr(dod, last_month=last_month, final_sim_year=final_sim_year))Now that we’ve generated the variables we want, let’s create a simple function that we can loop through.
#Estimate annual kin loss for women aged 25-39 in a particular year
getKinLoss <- function(year_of_interest,
opop = opop, omar = omar){
pid_data <- opop %>%
#Remove those not alive in the year of interest
filter(data.table::between(lower = dob_year, upper = dod_year,
year_of_interest, incbounds = FALSE),
#Filter to women
fem == 1) %>%
#Find the age of individuals alive
mutate(age = year_of_interest - dob_year) %>%
#Filter to women aged 25-39
filter(data.table::between(lower = 25, upper = 39, age,
incbounds = TRUE))
#Find vector of person IDs
pid_vec <- pid_data$pid
#Use the built-in retrieve_kin function
#We will not identify extended kin relationships (extra_kintypes)
#Or separate kin by sex, but both can be estimated
kin <- rsocsim::retrieve_kin(opop = opop, omar = omar, pid = pid_vec,
extra_kintypes = NULL, kin_by_sex = FALSE)
#From retrieve_kin, we get a list of lists named after the type of kin
#We loop over all types of kin included
temp <- bind_rows(lapply(1:length(kin), function(x) {
#Find IDs of kin
kin2 <- unlist(kin[[x]], use.names = FALSE)
#Attach associated person IDs
names(kin2) <- rep(pid_vec, unlist(lapply(kin[[x]], length)))
#Find the years of birth of kin
attr(kin2, "kin.dob.year") <- opop$dob_year[match(kin2, opop$pid)]
#Now find the years of death of kin
attr(kin2, "kin.dod.year") <- opop$dod_year[match(kin2, opop$pid)]
#Use this to find which kin were alive in the previous year
attr(kin2, "kin.alive.before.year_of_interest") <-
if_else(data.table::between(lower = attr(kin2, "kin.dob.year"),
upper = attr(kin2, "kin.dod.year"),
(year_of_interest-1), NAbounds = NA,
incbounds = FALSE),
TRUE, FALSE)
#And use that to find which kin have died in this year
attr(kin2, "kin.death.year_of_interest") <-
if_else(attr(kin2, "kin.dod.year") %in% year_of_interest, TRUE, FALSE)
#Find the number of people who had a living relative in the previous year
pid.withkin <- length(unique(names(kin2[attr(kin2,
"kin.alive.before.year_of_interest")
== TRUE])))
#Find the number of individuals who have lost a relative
pid.losekin <- length(unique(names(kin2[attr(kin2, "kin.death.year_of_interest")
== TRUE])))
#Find the total number of individuals
pid.total <- length(pid_vec)
#Generate output as a tibble
output <- tibble(kintype = names(kin[x]),
year = year_of_interest,
n_total = pid.total,
n_losekin = pid.losekin,
n_withkin = pid.withkin,
pc_losekin_total = 100*(n_losekin/n_total),
pc_withkin = 100*(n_withkin/n_total))
return(output)
}))
}Now loop through this function to generate a table with our data for each year. To limit the time this code will take to run, we’ll look estimate kin loss at 10-year intervals between 1950 and 2010.
#Loop through and bind rows
full_data <- bind_rows(lapply(seq.int(from = 1950, to = 2010,
by = 10),
function(x) getKinLoss(year_of_interest = x,
opop = opop,
omar = omar)))#Clean this data slightly
kinloss_data <- full_data %>%
#Clean names of kin
mutate(kintype = if_else(kintype == "ggparents", "Great-grandparents",
if_else(kintype == "gparents", "Grandparents",
if_else(kintype == "gchildren", "Grandchildren",
kintype))),
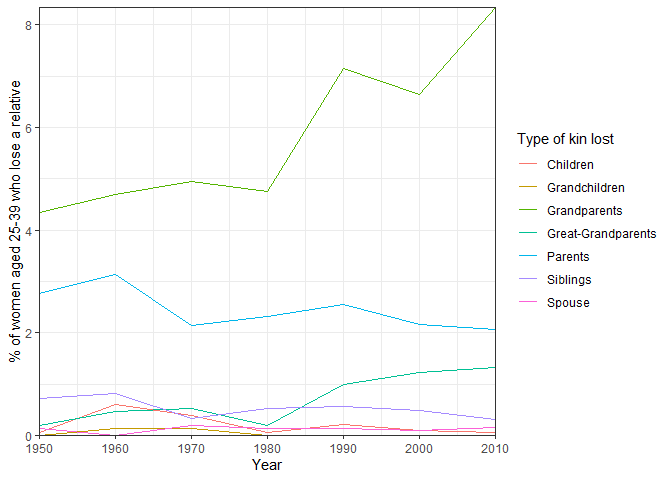
kintype = str_to_title(kintype)) Plot population-level kin loss over time.
kinloss_data %>%
#Create plot
ggplot(aes(x = year, y = pc_losekin_total, color = kintype)) +
geom_line() +
labs(x = "Year", y = "% of women aged 25-39 who lose a relative",
color = "Type of kin lost") +
#Fix the axes
scale_x_continuous(expand = c(0,0)) +
scale_y_continuous(expand = c(0,0)) +
#Set a theme
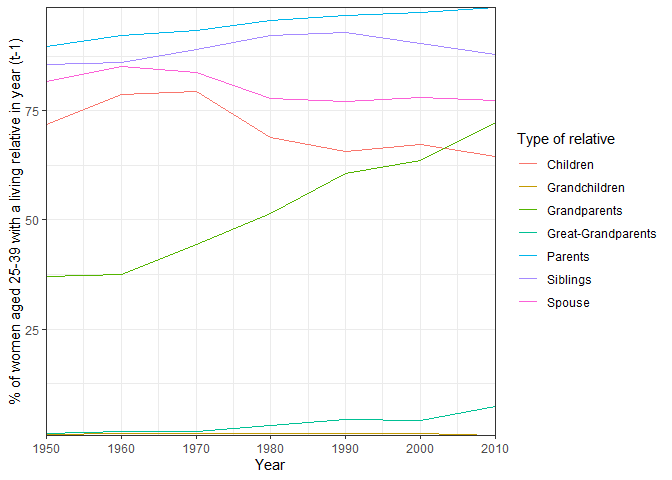
theme_bw() These results show us how rates of parental loss have changed for women over time: as we would expect for this age group, the highest rates of kin loss would be for grandparents and parents. The increasing rate of grandparental loss over time, along with a similar trend for great-grandparents, could relate to increasing life expectancies during this period: as grandparents live to older ages, the chance that an individual aged 25-39 has a living grandparent increases. This is brought out in the next plot, which shows changes in kin availability (the share of the population with a living relative in the year prior) over time.
#Plot changes in kin availability
kinloss_data %>%
#Create plot
ggplot(aes(x = year, y = pc_withkin, color = kintype)) +
geom_line() +
labs(x = "Year",
y = "% of women aged 25-39 with a living relative in year (t-1)",
color = "Type of relative") +
#Fix the axes
scale_x_continuous(expand = c(0,0)) +
scale_y_continuous(expand = c(0,0)) +
#Set a theme
theme_bw() To discuss: What are you interested in learning about, and how do you think SOCSIM could help you in your work?
The ‘SOCSIM Oversimplified’ manual written by Carl Mason (2016) is a great starting point to learn more about how SOCSIM works: https://lab.demog.berkeley.edu/socsim/CurrentDocs/socsimOversimplified.pdf.
You can find more information about the rsocsim in the package’s
website: https://mpidr.github.io/rsocsim/, including documentation for
the functions currently available and work in progress.
We are working on preparing extended vignettes with exercises and
examples for using rsocsim. Follow us on twitter for updates. Please
also get in touch if you’d like to use rsocsim for your work; we want
to hear from you!
- Tom Theile: https://twitter.com/TheileTom
- Diego Alburez: https://twitter.com/d_alburez
- Liliana P. Calderón-Bernal, https://twitter.com/lp_calderonb
- Mallika Snyder: https://twitter.com/mallika_snyder
- Emilio Zagheni: https://twitter.com/ezagheni
Alburez‐Gutierrez, Diego, Carl Mason, and Emilio Zagheni. 2021. “The ‘Sandwich Generation’ Revisited: Global Demographic Drivers of Care Time Demands.” Population and Development Review 47 (4): 997–1023. https://doi.org/10.1111/padr.12436.
Hammel, E. A. 2005. “Demographic Dynamics and Kinship in Anthropological Populations.” Proceedings of the National Academy of Sciences 102 (6): 2248–53. https://doi.org/10.1073/pnas.0409762102.
Hammel, E., D Hutchinson, K Wachter, R Lundy, and R Deuel. 1976. The SOCSIM Demographic-Sociological Microsimulation Program: Operating Manual. Institute of International Studies. University of California Berkeley.
HMD. Human Mortality Database. n.d. “Max Planck Institute for Demographic Research (Germany) and University of California, Berkeley (USA) and French Institute for Demographic Studies (France) Available at www.mortality.org.”
Human Fertility Database. n.d. “Max Planck Institute for Demographic Research (Germany) and Vienna Institute of Demography (Austria) Available at www.humanfertility.org.”
Margolis, Rachel, and Ashton M. Verdery. 2019. “A Cohort Perspective on the Demography of Grandparenthood: Past, Present, and Future Changes in Race and Sex Disparities in the United States.” Demography 56 (4): 1495–1518. https://doi.org/10.1007/s13524-019-00795-1.
Mason, Carl. 2016. “Socsim Oversimplified. Berkeley: Demography Lab, University of California.”
Snyder, Mallika, Diego Alburez-Gutierrez, Iván Williams, and Emilio Zagheni. 2022. “Estimates from 31 Countries Show the Significant Impact of COVID-19 Excess Mortality on the Incidence of Family Bereavement.” Proceedings of the National Academy of Sciences 119 (26): e2202686119. https://doi.org/10.1073/pnas.2202686119.
Verdery, Ashton M., and Rachel Margolis. 2017. “Projections of White and Black Older Adults Without Living Kin in the United States, 2015 to 2060.” Proceedings of the National Academy of Sciences 114 (42): 11109–14. https://doi.org/10.1073/pnas.1710341114.
Verdery, Ashton M., Emily Smith-Greenaway, Rachel Margolis, and Jonathan Daw. 2020. “Tracking the Reach of COVID-19 Kin Loss with a Bereavement Multiplier Applied to the United States.” Proceedings of the National Academy of Sciences 117 (30): 17695. https://doi.org/10.1073/pnas.2007476117.
Wachter, Kenneth W. 2014. Essential Demographic Methods. Harvard University Press.
Wachter, Kenneth W. 1997. “Kinship Resources for the Elderly.” Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences 352 (1363): 1811–17. https://doi.org/10.1098/rstb.1997.0166.
Wilmoth, J, K Andreev, D Jdanov, D. A. Glei, T Riffe, C Boe, M Bubenheim, et al. 2021. “Methods Protocol for the Human Mortality Database.” University of California, Berkeley; Max Planck Institute for Demographic Research, Rostock. https://www.mortality.org/.
Zagheni, Emilio. 2011. “The Impact of the HIV/AIDS Epidemic on Kinship Resources for Orphans in Zimbabwe.” Population and Development Review 37 (4): 761–83. https://doi.org/10.1111/j.1728-4457.2011.00456.x.