Dynax

Dynamic system in Jax (Dynax): This repo implements a differentiable simulator for building energy systems to support forward simulation, parameter inference and optimal control.

NOTE This library is still under active development. The APIs are not fully available yet.

This library solves the following general problem:

$$ \dot x_t = f_{xx} x_t + f_{xu} u_t $$

$$ y_{t} = f_{yx} x_t + f_{yu} u_t $$

or even more general format as

$$ \dot x_t = f_x(x_t, u_t) $$

$$ y_t = f_y(x_t,u_t) $$

The discrete format is shown as:

$$ x_{t+1} = f_{xx}x_t + f_{xu}u_t $$

$$ y_{t} = f_{yx}x_t + f_{yu}u_t $$

Software Architecture

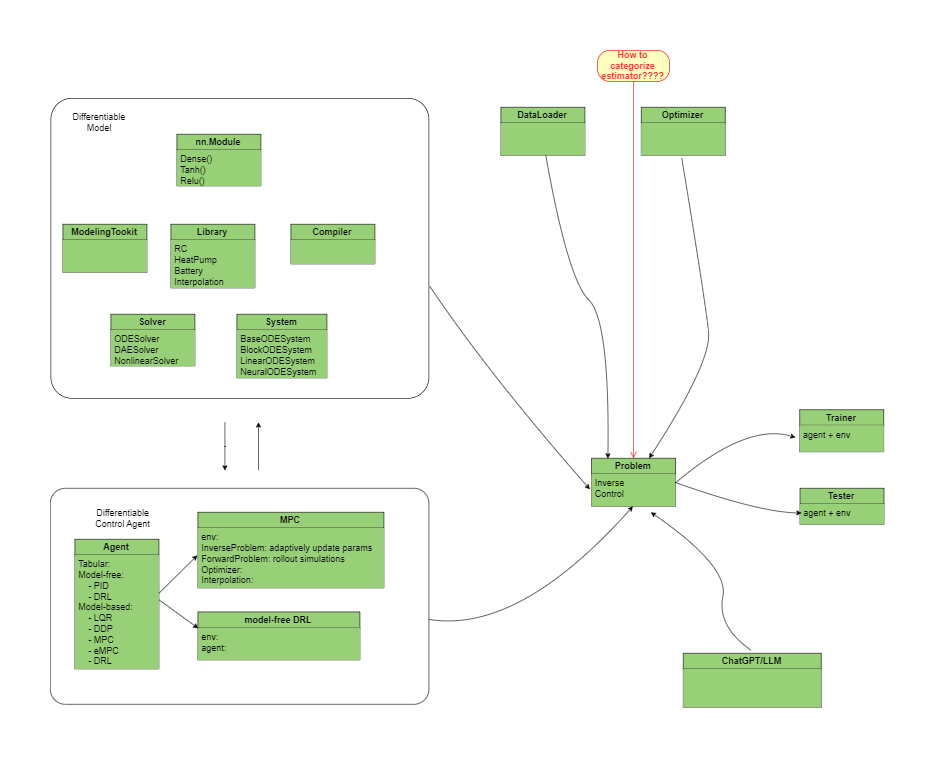
NeuralNetwork: a deep-learning framework based parametric programming module, e.g., pytorch, Flax etc.
DataLoader: prepare dynamic system data to trainable and testable data format
ModelingTookit: equation-based modeling tool
Compiler: compile models to ODE/DAE systems in pure mathematical representation
System: define unified system representation based on ODEs/DAEs, such as ODESystem, DAESystem, NeuralODESystem, ..., etc
NumericalSolver: define ODE/DAE integration solvers for solving dynamic systems that are typically represented as differential (algebriac) equations.
Problem: define a trainable problem, such as forward simulation, inverse simulation, implicit MPC, explicit MPC, model-based DRL, ..., etc
Optimizer: define an optimizer for the trainable problem, such as gradient descent
Trainer: define a training/learning process for a specific problem
TestCases: define some basic test cases to benchmark testing performance

JAX implementation

Toochain

Jax for basic auto-diff operations
Diffrax for numerical differentiable equation solvers in JAX
Sympy2jax for differential equation modeling in JAX
pydae using sundials
jax examples: https://ericmjl.github.io/dl-workshop/02-jax-idioms/02-loopy-carry.html

Julia implementation

Toolchain

Flux.jl
DifferentialEquation.jl
Optimization.jl

Applications

Forward Simulation

Deterministic Parameter Inference

Bayesian Inference

Probablistic Programming
Bayesian calibration
Bayesian optimization -> for control what is this?

Optimal Control

Dynamic Programming

LQR

MPC

The example shew with large RC, the first-order gradient method that requires tuning cannot generate sufficient precooling control sequence, which is counter-intuitive.

Implicit MPC

Explicit MPC

DRL

Model-based DRL to Support Value Iteration

Explicit Optimization Policy-based DRL

check the paper at https://web.stanford.edu/~boyd/papers/pdf/learning_cocps.pdf

and

B. Amos, I. Jimenez, J. Sacks, B. Boots, and J. Z. Kolter. Differentiable MPC for endto-
end planning and control. In Advances in Neural Information Processing Systems,
pages 8299{8310, 2018.

M. Okada, L. Rigazio, and T. Aoshima. Path integral networks: End-to-end differentiable
optimal control. arXiv preprint arXiv:1706.09597, 2017.

Use Cases (in design)

Base Model

RRN-style implementation of Base Model

[] add description

Model Definition (ODE format representation)

Define a model with ODE format. It could be a pure-physics based model or a neural ODE.

class Model(BaseSSM):
    param_initializer

    def setup(self):
        """ set up ode format here 
        """
        self.params = self.param('p1', initializer=self.param_initializer(), ...)
        self._fxx = fxx()
        self._fxu = fxu()
        self._fyx = fyx()
        self._fyu = fyu()
        self._fx = fx()
        self._fy = fy()

    def __call__(self, inputs):
        # rearrange inputs for hidden states, and inputs
        x, u = split(inputs)
        # return 
        return super().__call__(x, u)

    class fxx(nn.Module):
        ...
    class fxu(nn.Module):
        ...
    class fyx(nn.Module):
        ...
    class fyu(nn.Module):
        ...
    class fx(nn.Module):
        ...
    class fy(nn.Module):
        ...

Differentiable Simulator

This defines a simulator with given model. It should generate results for a given time period with given inputs.

class Simulator(BaseSimulator):
    
    model: nn.Module
    dt: float

    def __call__(self, states, inputs):

        def rollout(model, carry, scan):
            """ A rollout function for multi-steps simulation
            """
            ...
            x, y = model(inputs)
            ...
            return carry, (x, y)
        
        scanned_rollout = nn.scan(rollout, ....)
        carry_init = x0
        steps_for_scan = jnp.arange(ts, te, self.dt)
        _, (xsol, ysol) = scanned_rollout(self.model, carry_init, steps_for_scan)

        return xsol, ysol

Forward Simulation with given control sequences

This is an example to simulate cases where the control inputs are predefined over time as an external file, such as csv. This case is typical for inverse inference of a given model using existing data.

There could be two ways to perform forward simulation. One is using functional programming as follows.

from dynax.agents import Tabular
from dynax.models import BaseModel
from dynax.simulators import BaseSimulator

# define a dynamic model
class Model(BaseModel):
    ...

    def __call__(self, inputs):
        ...
        return super().__call__()

# define a simulator for the model
class Simulator(BaseSimulator):
    ...

# define simulation settings
ts = 0
te = 10
dt = 1.0

# given control and disturbance 
t, u = np.linspace(ts, te, 100), np.random.rand(100,2)
t, u = np.linspace(ts, te, 100), np.random.rand(100,4)
# implement a gather function to create inputs for dynamical model
inputs = gather(t, u,d)

# specify model
ode = Model(...)

# specifying a simulator
ds = Simulator(model=ode, dt=dt, ...)

# simulate the system
init_params = ds.init(jax.random.PRNGKey(0), inputs, ...)
xsol, ysol = ds.apply(init_params, inputs)

The other approach is to formulate the forward problem as a neural network layer.

class Forward(nn.Module):
    simulator: BaseSimulator

    def __call__(self, inputs, ts, te, ...):
        
        xsol, ysol = self.simulator(inputs, ts, te)

        return xsol, ysol
# specify differentiable simulator
model = Model(...)
simulator = Simulator(...)
# formulate forward problem
forward = Forward(...)

# solve forward problem
init_params = forward.init(jax.random.PRNGKey(0), inputs, ts, te, ...)
xsol, ysol = forward.apply(init_params, inputs, ts, te, ...)

Forward Simulation with Feedback Control

Functional programming:

from dynax.agents import PID

# specify model and simulator instance
model = Model(...)
simulator = Simulator(...)
policy = PID(...)

# experiment settings
ts = 0
te = 10
dt = 1

## simulation loop
y_init = ...
yt = y_init

# initialze simulator
init_params = simulator.init(....)

while t < te:
    # reference signal
    ys = reference(t)
    # control signal from policy
    ut = policy(yt, ys)
    # other inputs 
    dt = disturbance(...)

    # gather for model inputs
    inputs_t = gather(ut, dt, ...)

    # step
    xt, yt = simulator.apply(init_params, inputs, t, t+dt)

    # update step
    t += dt

Forward simualtion with closed loop control as a neural network layer

[] add design

Inverse Simulation

The inverse simulation can be formulated base on a learnable forward problem. Here take as an example a calibration problem

from dynax.dataloader import DataLoader
from dynax.agents import Tabular
from dynax.optimizers import GradientDescent
from dynax.trainers import Trainer
from dynax.trainers import TrainStates

# define a forward problem first
forward = Forward(...)

# define states for inverse problem
class InverseTrainStates(TrainStates):
    parameter_lb
    parameter_ub

# define an optimizer
optim = GradientDescent()

# create train states
train_states = InverseTrainStates.create(
    forward = forward.apply,
    params = params_init,
    tx = optim, 
    ...
)

# load train and test data
data_loader = DataLoader(...)
train_ds = data_loader.train
test_ds = data_loader.test


# train step
@jax.jit
def train_step(train_state, ..., target):
    
    # define a loss function for calibration
    def loss_fn(params):
        y_pred = train_state.forward(params, ...)
        error = jnp.sum((target - y_pred)**2)

        regularizer = (...)
        return error + regularizer

    loss, grads = jax.value_and_grad(loss_fcn)(train_state.params)
    train_state = train_state.apply_gradients(grads=grads)

    return loss, grads, train_state

# specify a gradient descent optimizer
optimizer = GradientDescent()

# training
n_epochs = 100
for epoch in range(n_epochs):
    for (x, target) in train_ds:
        loss, grads, train_state = train_step(train_state, ..., target)

# final parameters
params_final = train_state.params

Gym Wrapper

This module provides a general differentiable and jittable wrapper for differentiable simulators. The jittable capability can speed up rollout simulations in a magnitude of 10x-100x.

Key highlight usages are as follows:

import jax 
import flax.linen as nn
from dynax.wrapper.envs.rc import RC

# basic OpenGym-like interface
env = RC(...)

seed = 0
key = jax.random.PRNGKey(seed)
obs, states, params = env.reset(key)
action = env.action_space.sample(key)
obs, reward, terminate, truncated, info, states = env.step(action, states, params)

# jittable functional interface
env = RC(...)
obs, states, params = jax.jit(env.reset)(key)
action = jax.jit(env.action_space.sample)(key)
obs, reward, terminate, truncated, info, states = jax.jit(env.step)(action, states, params)

# jittable module
env = nn.jit(RC)(...)
obs, states, params = env.reset(key)
action = env.action_space.sample(key)
obs, reward, terminate, truncated, info, states = env.step(action, states, params)

# vectorized env 
n_parallel = 10
env = RC(...)
keys = jax.random.split(key, n_parallel) # 10 different seeds
obs, states, params = jax.vmap(env).reset(keys) # different initial states if suppored from different reset()
action = jax.vmap(env.action_space.sample)(keys) # different actions
obs, reward, terminate, truncated, info, states = jax.vmap(env.step)(action, states, params) # parallel steps

Optimal Control: MPC

from dynax.dataloader import DataLoader
from dynax.agents import MPC
from dynax.utils import LinearInterpolation
from dynax.estimators import LeastSquareEstimator
from dynax.systems import LinearODESystem
from dynax.solvers import Euler
from dynax.problems import InverseProblem
from dynax.optimizers import GradientDescent
from dynax.trainers import Trainer
from dynax.trainers import TrainStates

import gymnasium as gym
from envs import building

# load data
data_loader = DataLoader()
data_loader.load_data('data/linear_ode.csv')

# specify a piecewise constant control/disturbance agent
disturbance = LinearInterpolation(data_loader.t, data_loader.d)

# specify a linear ODE system
lode = RCModel()

# specify a numerical solver
solver = Euler()

# specify a simulator
ds = Simulator(lode, solver)

# specify a least square estimator
estimator = LeastSquareEstimator()

# loss function
def loss_fn(y, y_hat):
    return np.sum((y - y_hat)**2)

# specify a gradient descent optimizer
optimizer = GradientDescent()

# specify an implicit MPC control problem
mpc_problem = ImplicitMPCProblem(ds, estimator, params, loss_fn, data_loader, optimizer)

# specify a virtual environment with measurement nosie if possible
env = gym.make('building-v0')

# specify a trainer
trainer = Trainer(mpc_problem, env)

# train the model
trainer.train(data_loader)

# test the model
tester = Tester(mpc_problem, env)
tester.test(data_loader)

Optimal Control: DRL

from dynax.agents.drls.offpolicy import DDQN

Contact

Yangyang Fu

fuyy2008@gmail.com

YangyangFu / dynax