Project C++ - Équation de la chaleur

Préliminaires

Modifier le CMakeLists.txt à la racine pour spécifier une version de Python installée qui possède numpy, faire de même sur src/utils/CMakeLists.txt (c'est pour la libraire matplotlib-cpp).

Pour compiler:

mkdir build/
cd build/
cmake ..
cmake --build .
./src/mines-cpp-chaleur

Question 2

Dans la racine du projet:

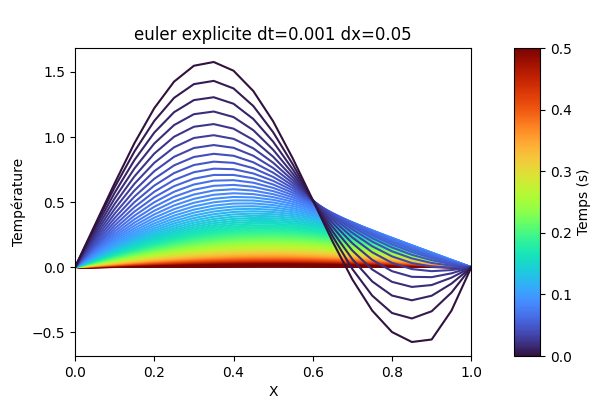
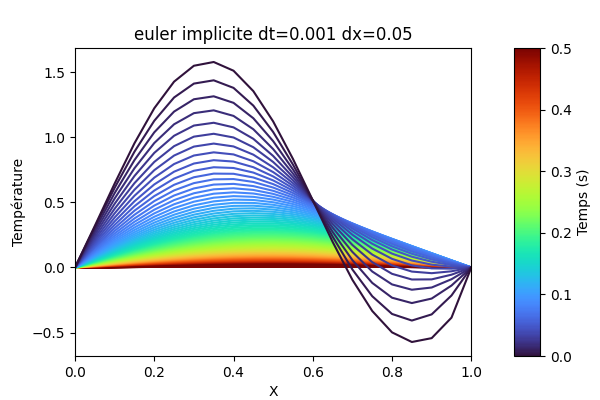
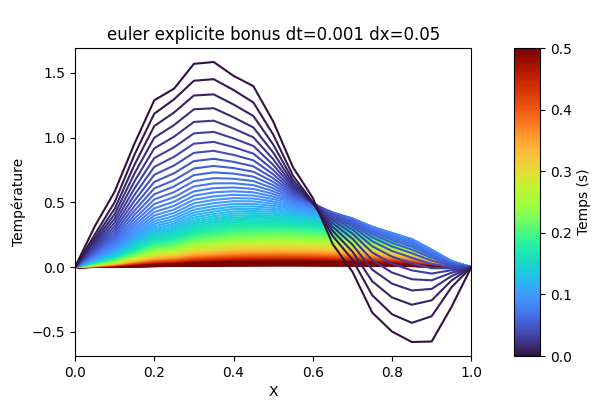
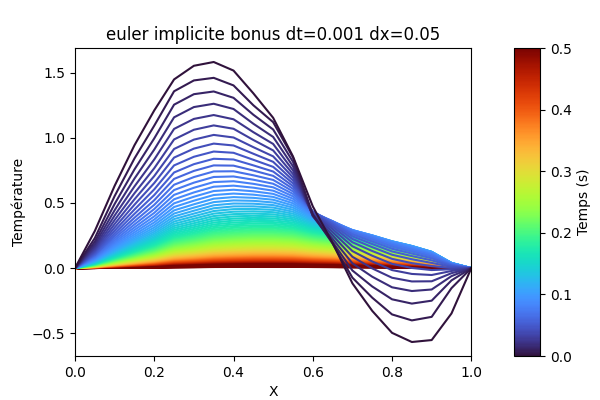
python3 graph.py build/euler_explicite.txt

Question 4

python3 graph.py build/euler_implicite.txt

Question Bonus 1

python3 graph.py build/euler_explicite_bonus.txt

python3 graph.py build/euler_implicite_bonus.txt

Question Bonus 2

--- Performance avec dx=0.1 et dt=0.005
Euler explicite: 1.1 ms
Euler explicite creux: 4.4 ms
Euler implicite: 2 ms
Euler implicite creux: 7 ms
--- Performance avec dx=0.05 et dt=0.00125
Euler explicite: 13.6 ms
Euler explicite creux: 76.6 ms
Euler implicite: 21.9 ms
Euler implicite creux: 113.8 ms

Euler explicite est plus rapide que Euler implicite, ce qui était attendu
L'implémentation de la matrice creuse n'est pas satisfaisante. J'ai d'abord essayé d'utiliser des matrices creuses pour tous les vecteurs, mais c'était encore plus lent. J'ai donc mis $K$ en SparseMatrix uniquement.
- Il faudrait utiliser une fonction de Eigen pour résoudre le système linéaire, à la place de ma propre implémentation.

Question Bonus 3

L'animation effectuée avec la librairie matplotlib-cpp s'affiche à l'éxécution.

Tests

Dans le ./build, après compilation:

./tests/mines-cpp-chaleur_tests

Notes

Pratiques

Le code (noms de variables, classes, fichiers) est en anglais. Les commentaires sont en français.
La documentation pour une fonction est au dessus des déclarations dans les fichiers .h, ou s'ils n'existent pas dans le .cpp directement.
L'indexation des matrices commence à 0.
Les librairies sont directement dans le repo.

Théoriques

(PS: le latex ne s'affiche que dans VS Code)

Choix de $\Delta x$ et $\Delta t$

Pour pouvoir obtenir des résultats correct avec la méthode d'Euler explicite, il faut respecter la condition de stabilité:

$$\Delta t \leq \dfrac{(\Delta x)^2}{2max(D)}$$

Il n'y a aucune contrainte dans le cas de la méthode implicite.

Clarification de l'énoncé

Petits changements effectués aux équations de l'énoncé:

Inversion de signe devant la matrice $K$ telle qu'elle est définie
Il faut diviser par $(\Delta x)^2$ (corrigé dans la version 2 du sujet).
Pour pouvoir garantir le respect des conditions aux bords ($\forall t, T(0, t) = T(L, t) = 0$) j'ai changé la première et dernière ligne pour qu'elles "copient" simplement la première et dernière case de $T_{i}$ sur $T_{i+1}$.
- C'est nécessaire car sinon $K$ n'est pas bien définie ($D_{i+1}$ pour $i = n$ n'existe pas)

La matrice $K$ est donc la même que dans l'énoncé, mais avec (1, 0, 0, ...) comme première ligne et $(..., 0, 0, 1) comme dernière ligne.

Les équations utilisées sont les suivantes:

Euler explicite: $(I_n + \dfrac{\Delta t}{(\Delta x)^2})T_{i+1} = T_{i}$

Euler implicite: $T_{i+1} = T_{i} + \dfrac{\Delta t}{(\Delta x)^2}KT_{i}$

Méthode de résolution

J'ai eu du mal à utiliser sereinement le gradient conjugué, sachant que l'algorithme n'est destiné en théorie qu'aux matrices symétriques positives définies. La matrice de l'énoncé est symétrique mais non positive
- Cette méthode semble tout de même fonctionner sur la matrice utilisée pour $D : x \mapsto 1$
- J'ai essayé le l'appliquer au système $A^TA = A^Tb$, ce qui en théorie respecte toutes les hypothèses ($A^TA est sym. def. pos., si $A$ est inversible) mais ça ne marchait pas souvent (le conditionnement est sûrement trop important)
Cependant, la matrice étant toujours tridiagonale, j'ai finalement choisi d'utiliser l'algorithme de Thomas

Performance

-- Solver performance tests, N = 50
Tridiagonal mean: 0.136 ms
Conjugate gradient mean: 22.7507 ms

C'est pour des matrices tridiagonales aléatoires, le gradient conjugué est désavantagé car on ne peut pas prendre x0 proche de la vraie solution dans ce benchmark. L'avantage de l'algorithme de Thomas est qu'on sait exactement le nombre d'itération qu'il prendra, en fonction de la dimension.

TrakJohnson / mines-cpp-chaleur