Matthias Möller
There is a little game on Steam: The Button by Elendow.
The advertisement promises the following:
Steam page description
Every time you press the button you get 1 point. Every time you press the button your odds to lose all your points increases by 1%. Good luck.
Obviously, this is a lot information to process at once. You start with
some starting probability
If you don’t loose tho, you did everything right. You are 1 round
further, the sun shines on the brilliant head of yours because not
everyone was able reaching the point where you are. But don’t be in this
heightened state of happiness for too long, because you have a
decision to press the button again. There is no other way, you have to
go trough it again! But this time, “your odds to lose all your points
increases by 1%”. Oh god, no! What does it even mean? Is the new
Nobody likes misunderstandings, but as I said, there is no choice. We can only press the button, again! and again! and again! until we, inevitable, loose (or run away). Oh what a tragedy, such a cruel world. This game is like the life itself, you press buttons until you loose, or is it?
As every normal human being, we should question everything. In particular we should question this game! What if the advertisement text lies to us? Wouldn’t be the first time. Maybe the whole game is a trap? Maybe we don’t loose every time but the probability that we loose decreases by 1%? Some people would be in an endless game of button pressing when they reach 100%. Oh no, this would be cruel and if this is the case, we have to warn everyone!
There is one guy, deedeedont, on Steam
Community
who thinks he solved the game already by mentioning, that the
probability is
It is obvious, that we cannot just answer all these question. There is sadly only one way1 to answer them, we have to:
That’s right, we have to do it on our own. How can we measure probabilities? Simple, just take samples. A lot. Do some math and claim that this is true, that your sample size is big enough and that black swans are heresy and everyone who proclaims otherwise will be handled… for the emperor, blood for the blood god etc.
Anyway, let’s assume that the game always behaves equally on every run
(otherwise, we are doomed anyway, because of the heresy). Then we can do
We can either collect the data by hand, but this sounds like boring work. Nobody likes boring work and we all are not nobody (except nobody).
We all love PCs, because they can do work, we don’t want to do. Therefore, there is a little program in this repository which can do the work for us.
This program will simply capture every image on screen #1, limit the image so that only the button is visible. Do some OpenCV stuff to extract the numbers (you need the red! button, no other color) and recognize the extracted numbers. It reports the number in a csv file. Afterwards, it auto clicks in the middle of the screen.
At the end, it prints statistics in another csv which summarizes, how often a number was seen during the runs.
It is kinda an ugly duckling and currently just calibrated to my display (3440x1440), you have to change the coordinates by yourself so that only the button is in the ROI.
The image processing is kinda fast (~200microseconds on my machine), but waiting for a new number after the mouse has been “auto”-clicked, takes long. We have to wait around 300ms starting the click up until we see a new number.
With this program, it is possible for us to have multiple runs.
I, for both of us, let it run for around 10k rounds. The raw data is also in the repository under data.
Just for your entertainment, lets have some look at the collected data. First, of all, the data shows me that the game requires 77.7MB?! For a button! You want a button? Here, have a button! You can style it, give it a golden color, make it bigger, smaller and customize it’s reactions etc. in less than 77.7MB. You can even attach my program towards it, it will be still less than 77.7MB.
For the runs, I saved the csv files, which are both combined are also less than 77.7MB! he 77.7MB must contain secrets!
I got sidetracked, back to the data.
The out.csv file just contains every number the program saw before each button press. The csv let your bleed your eyes, as it has only 1 column. I am just slightly sorry for that format, just don’t look at it as it is just there to have raw data and the second one is more interesting.
The second, stats.csv, has the count of seen number grouped by the number.
With this, we can very simple compute the probability for every step, by
simply dividing the amount of occurrences we counted on round n and
divide it with the amount of occurrences we counted for round n+1:
stats$p_n <- stats$counts / list(1000, stats$counts[1:nrow(stats)-1]) %>% simplify()
stats$expected_diff <- abs(stats$p_n - stats$expected)
colnames(stats) <- c("n", "counts", "expected p", "measured p", "expected - measured")
kable(head(stats, n=15))| n | counts | expected p | measured p | expected - measured |
|---|---|---|---|---|
| 0 | 1000 | 1.00 | 1.0000000 | 0.0000000 |
| 1 | 1000 | 1.00 | 1.0000000 | 0.0000000 |
| 2 | 992 | 0.99 | 0.9920000 | 0.0020000 |
| 3 | 966 | 0.98 | 0.9737903 | 0.0062097 |
| 4 | 929 | 0.97 | 0.9616977 | 0.0083023 |
| 5 | 895 | 0.96 | 0.9634015 | 0.0034015 |
| 6 | 842 | 0.95 | 0.9407821 | 0.0092179 |
| 7 | 790 | 0.94 | 0.9382423 | 0.0017577 |
| 8 | 726 | 0.93 | 0.9189873 | 0.0110127 |
| 9 | 660 | 0.92 | 0.9090909 | 0.0109091 |
| 10 | 597 | 0.91 | 0.9045455 | 0.0054545 |
| 11 | 541 | 0.90 | 0.9061977 | 0.0061977 |
| 12 | 482 | 0.89 | 0.8909427 | 0.0009427 |
| 13 | 418 | 0.88 | 0.8672199 | 0.0127801 |
| 14 | 366 | 0.87 | 0.8755981 | 0.0055981 |
As we can see from the little table, the calculations confirm our expectations where the sample size is big enough. The smaller the sample size, the bigger is our observation error due to under sampling.
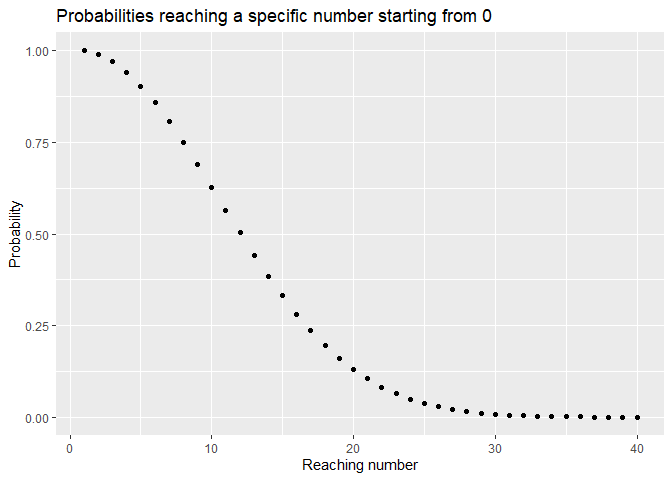
Or, if you are more someone who likes drawn images instead of boring dusty tables.
runs <- 40
run_probas <- data.frame(run_to=seq(1,runs),prob_reaching=cumprod(seq(100, 100-(runs-1), -1)/100))
ggplot(run_probas, aes(x=run_to,y=prob_reaching)) + xlab("Reaching number") + ylab("Probability") + ggtitle("Probabilities reaching a specific number starting from 0") + geom_point()This looks like a nice slope downwards! We can have fun riding it down, but remind you, that it also shows the future. Every time you press the button, your next future looks less likely to be a win. It might ruin your fun, but maybe it is also something your are looking for.
We can simply conclude that there is no surprise, nothing new, everything is as expected. No secret, no UFO, nothing hidden. It is like you pressed a button for a long time and in the end, you lost. That’s it.
A bit disappointing, isn’t it? No not really! We were able to confirm our believes and were able to transform believes into knowledge (with a given probability that the black swan does not exist, like human-tall rats don’t exist!).
All we can do is stop pressing the button and therefore stop loosing all the time and use the slope as a nice water slope enjoying the summer.
But, can we?
Good night, Stanley.
Footnotes
-
OK, there are maybe other ways like asking the developer, but this would not solve the advertisement trust issues or that we have to interact with a human stranger. Yikes. ↩