Updated version of this repository can be found here.
FDM (Finite Difference Method) simulation of 2D lid-driven cavity flow based on :
- fractional step method for time integration
- Kawamura-Kuwahara scheme (3rd-order upwind -> 4th-order central with 4th-order numerical viscosity) for convection
- 2nd-order central difference for pressure gradient and viscosity terms
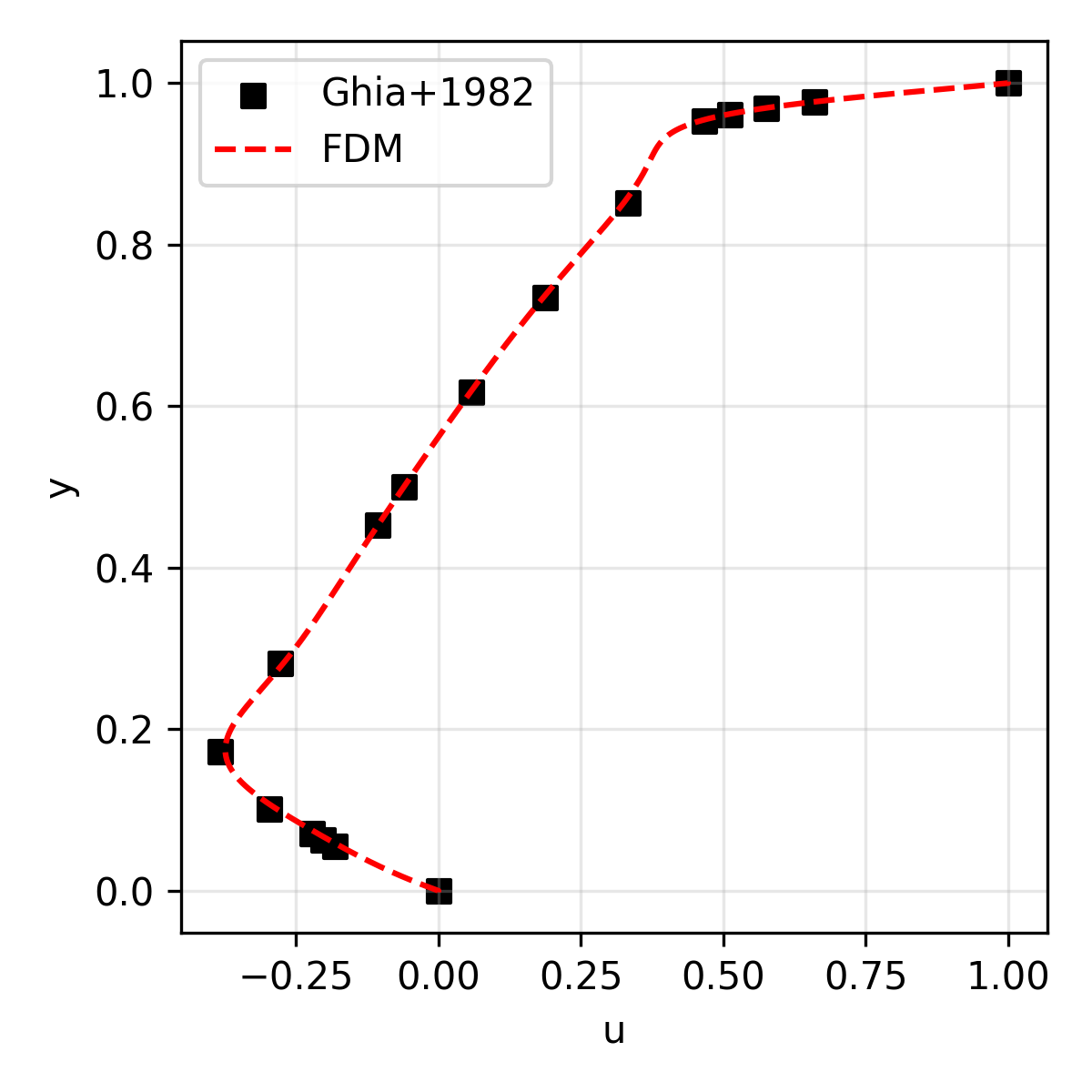
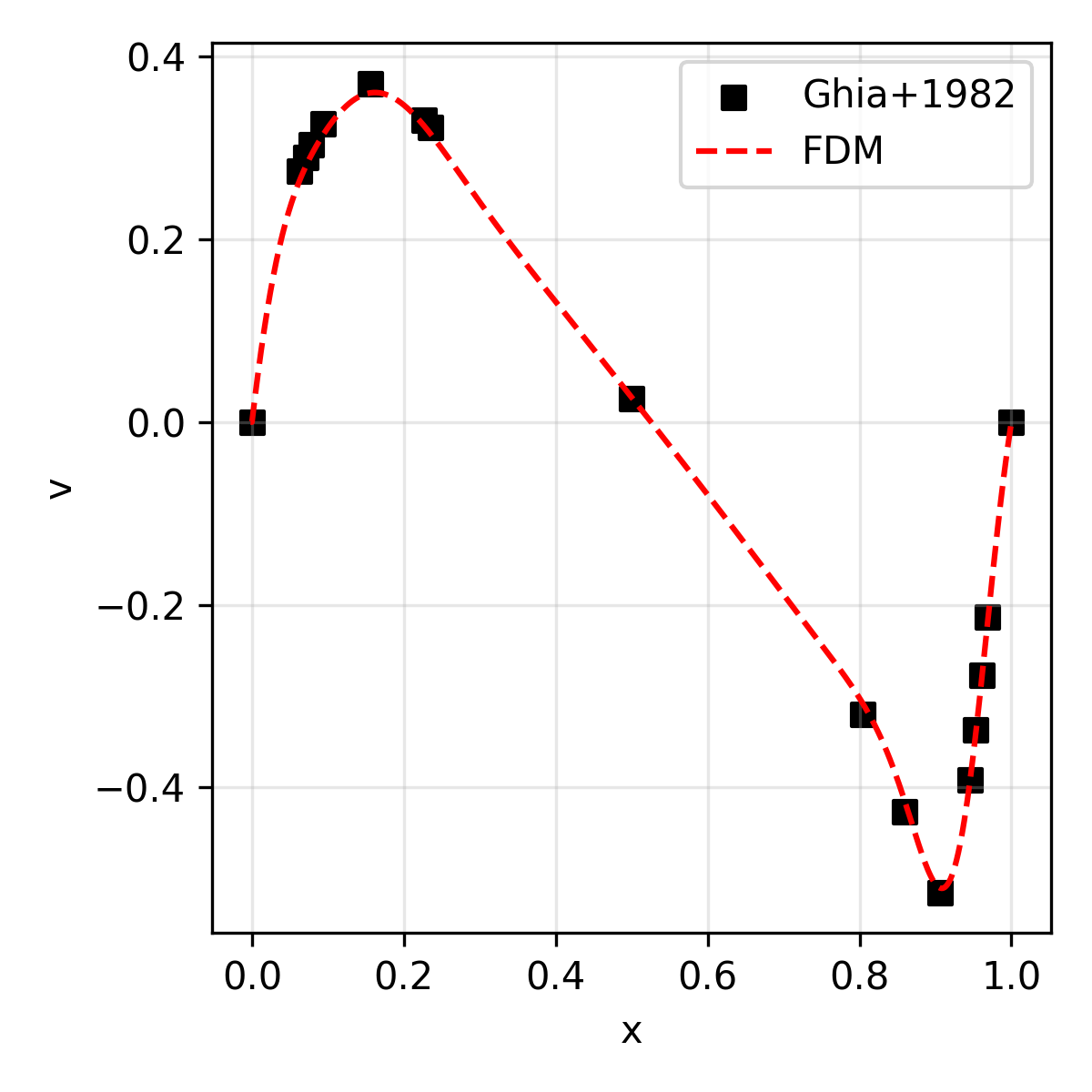
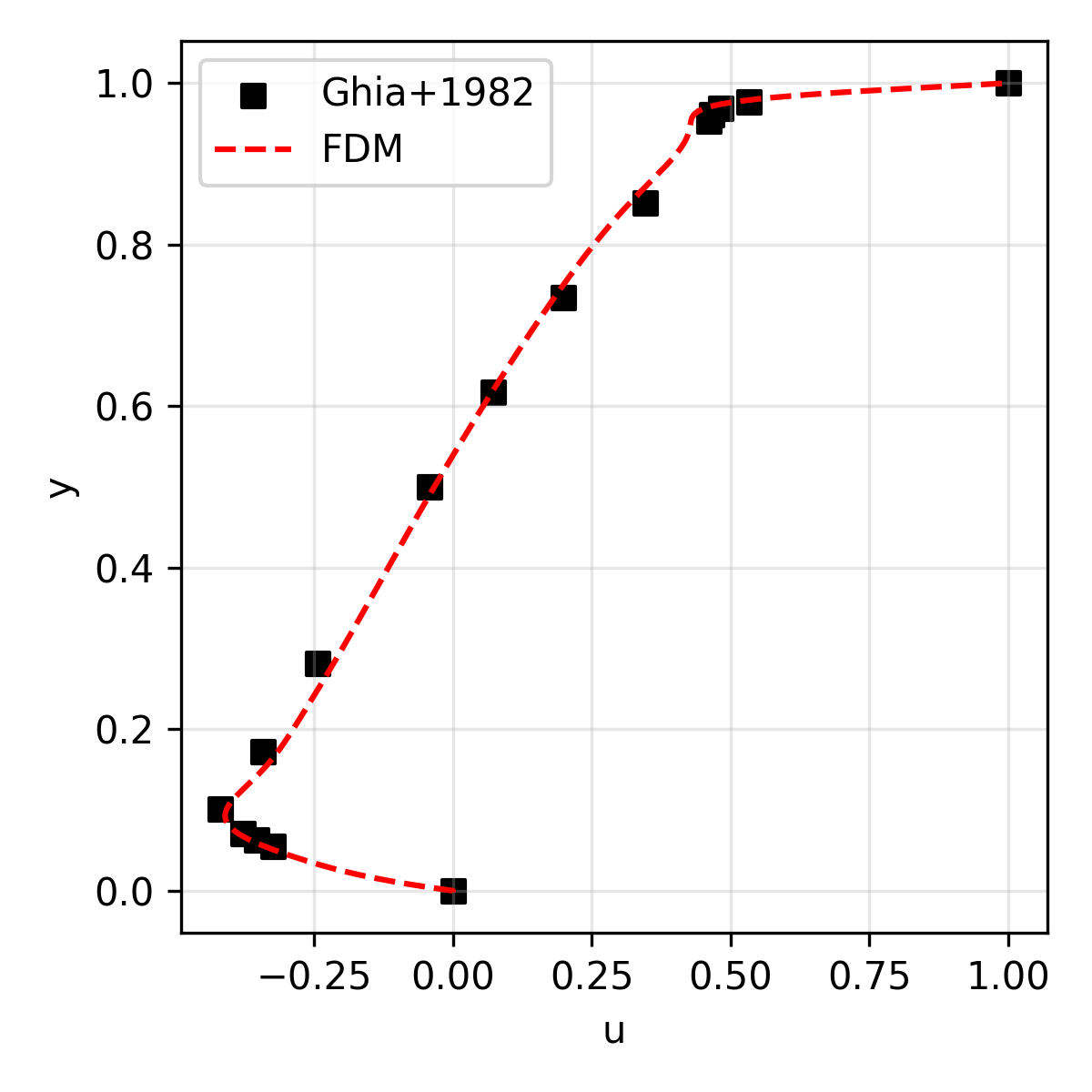
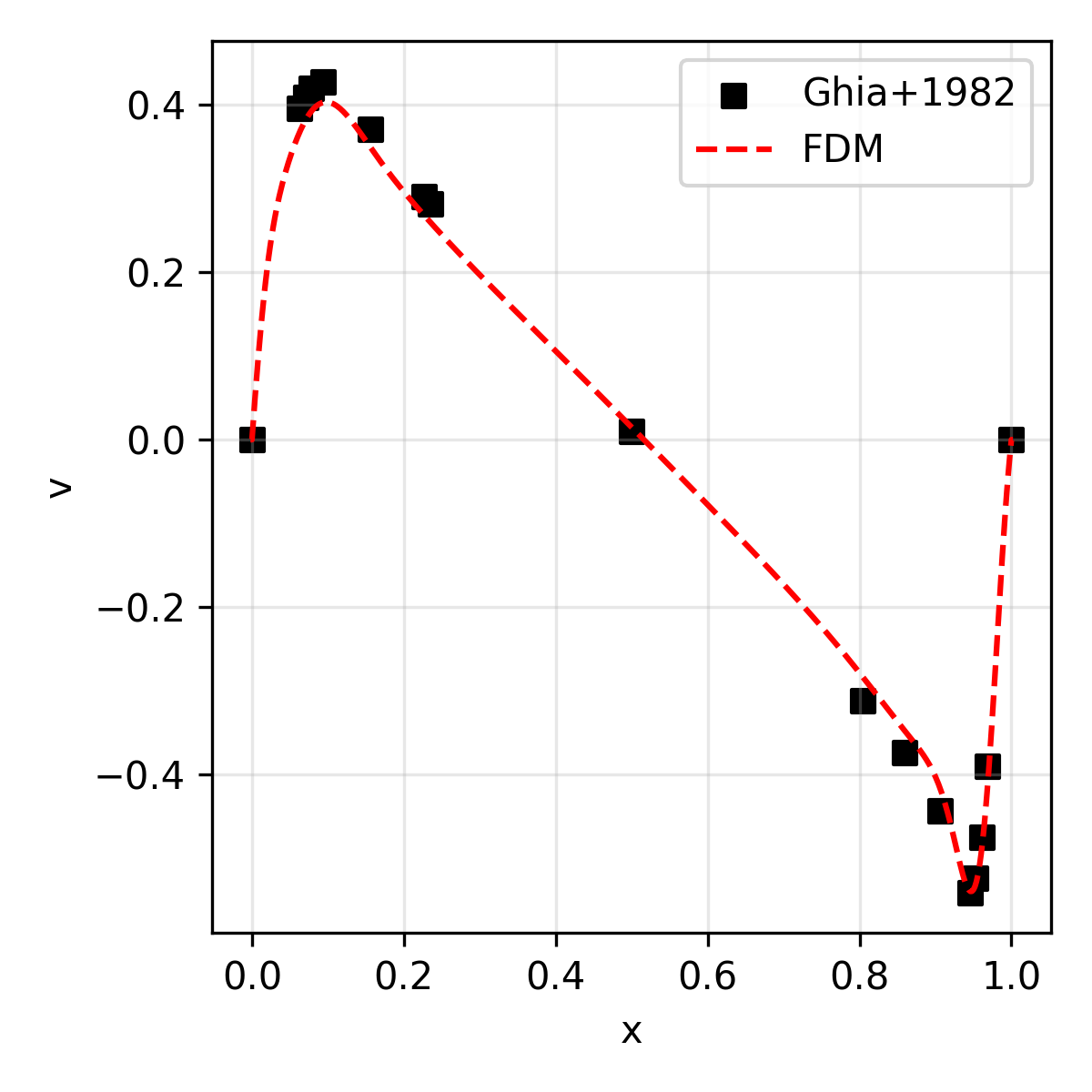
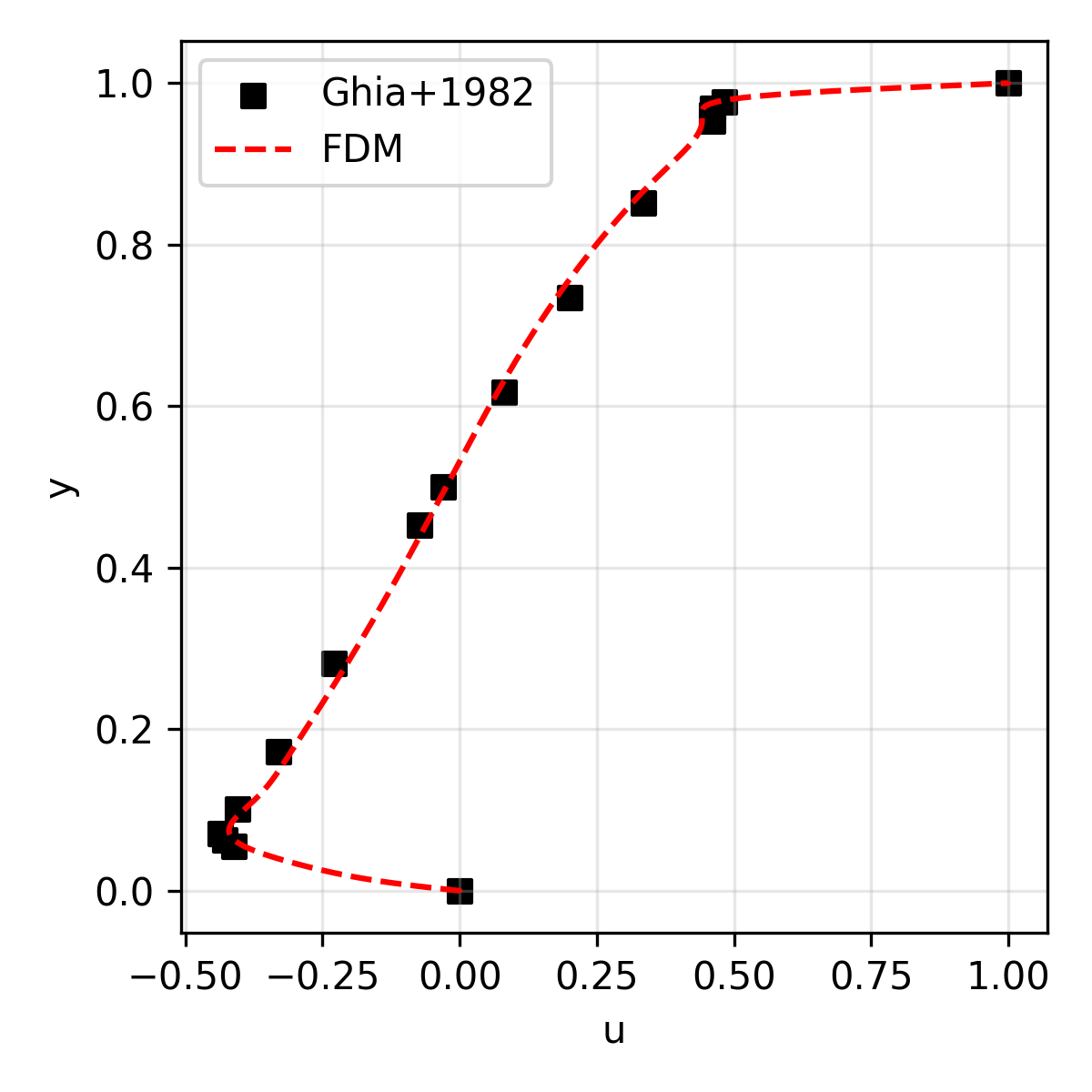
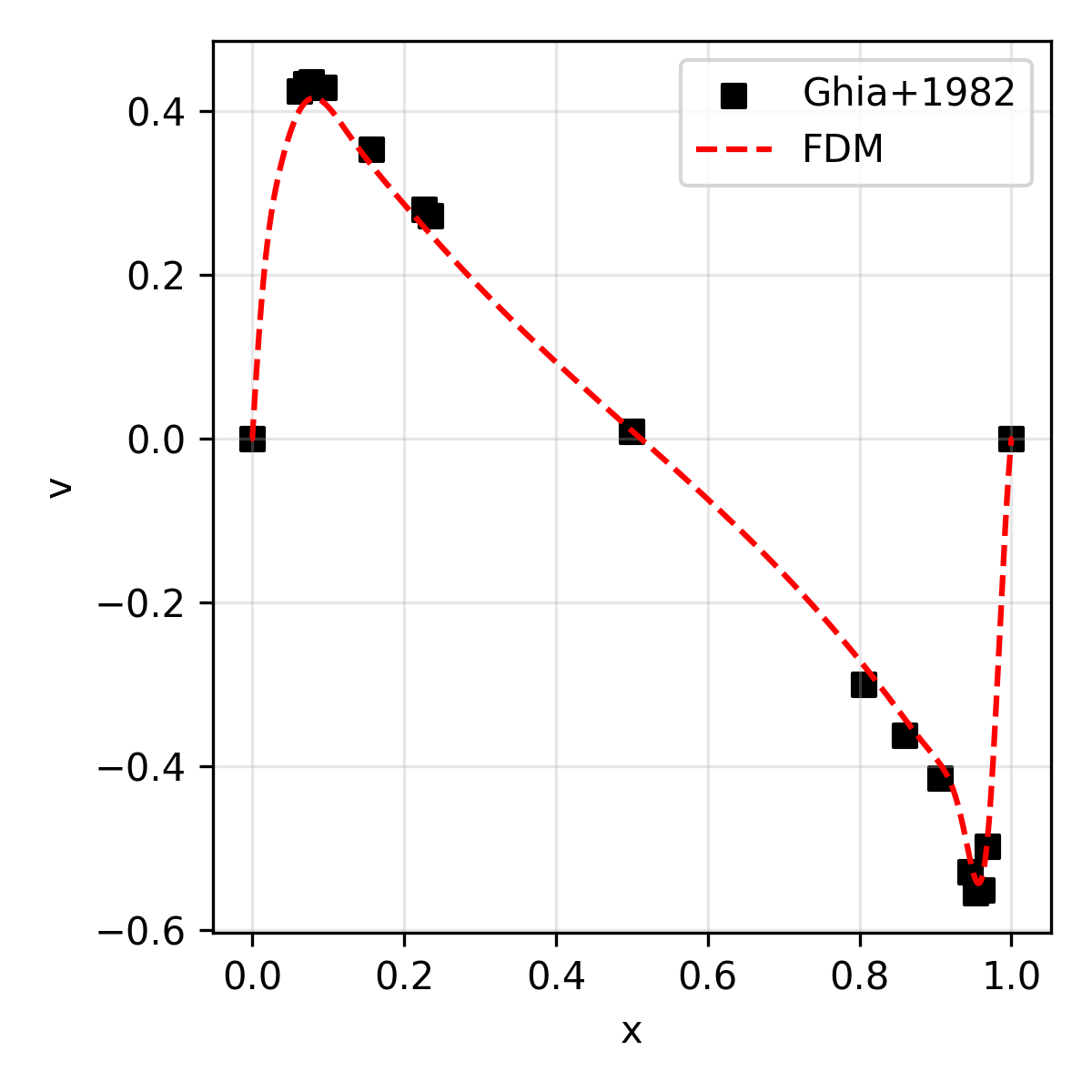
The results are compared with the reference solution (for velocity) presented in Ghia+1986.
Cavity flow is a steady problem. We consider that the field has reached to a steady state when the following is satisfied:
where
The following summarizes results at different Reynolds numbers and different resolutions.
| Column name | Description |
|---|---|
| Re | Reynolds number (inertia vs viscosity) |
| t | Dimensionless time until the convergence (when velocity residual |
| u | Horizontal velocity along the geometric center |
| v | Vertical velocity along the geometric center |
| Re | t | Velocity norm | Pressure | u | v |
|---|---|---|---|---|---|
| 100 | 15.4 | 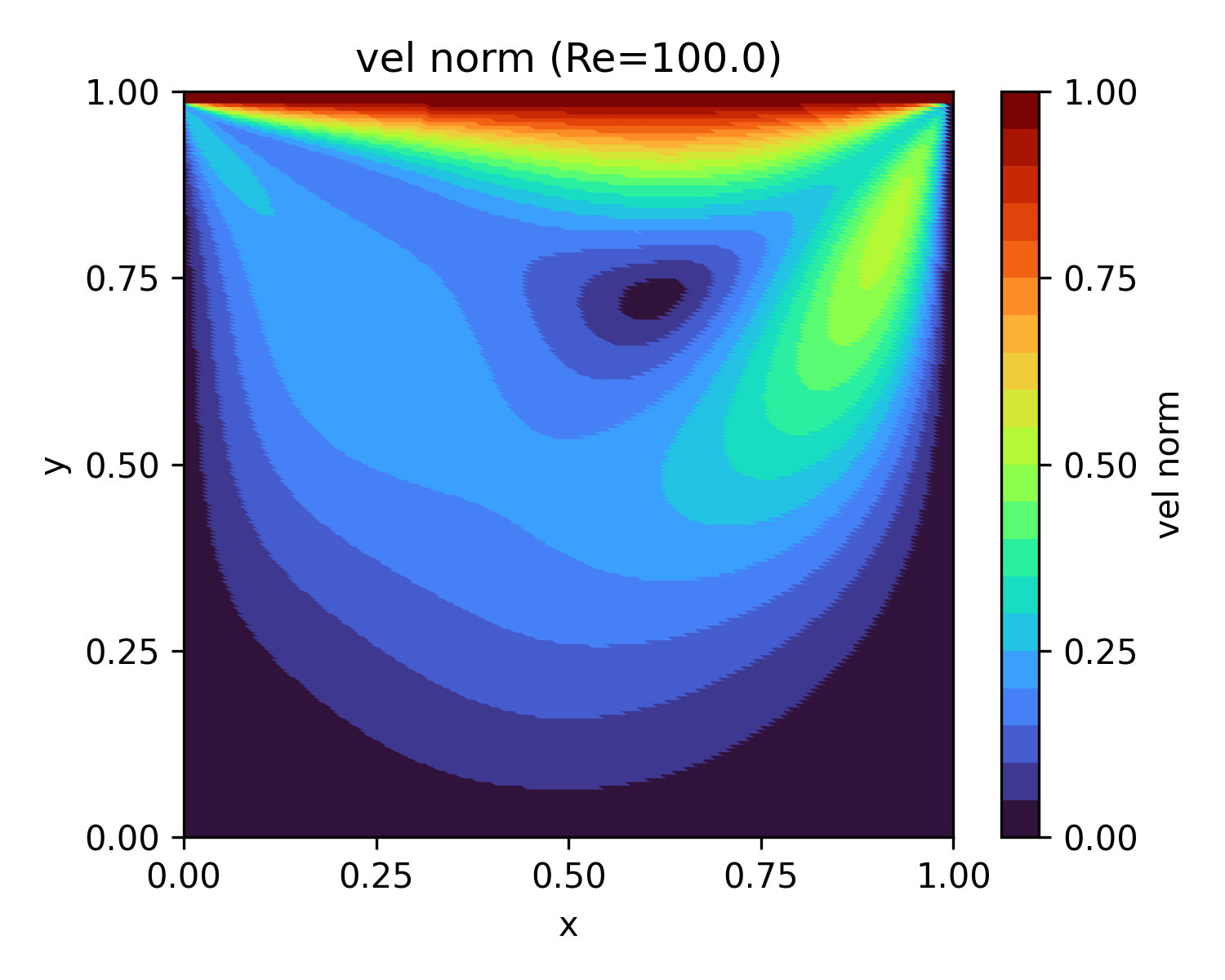 |
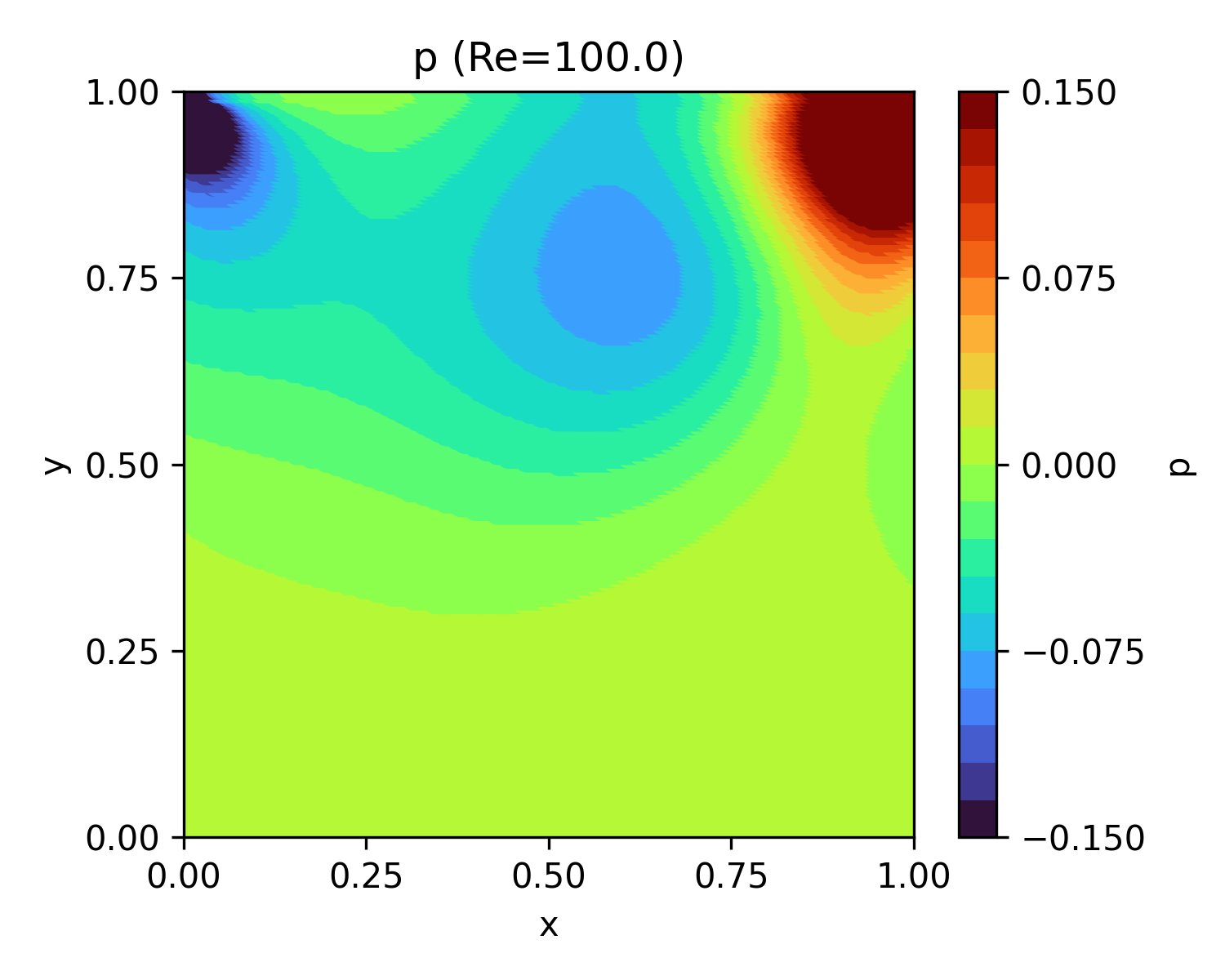 |
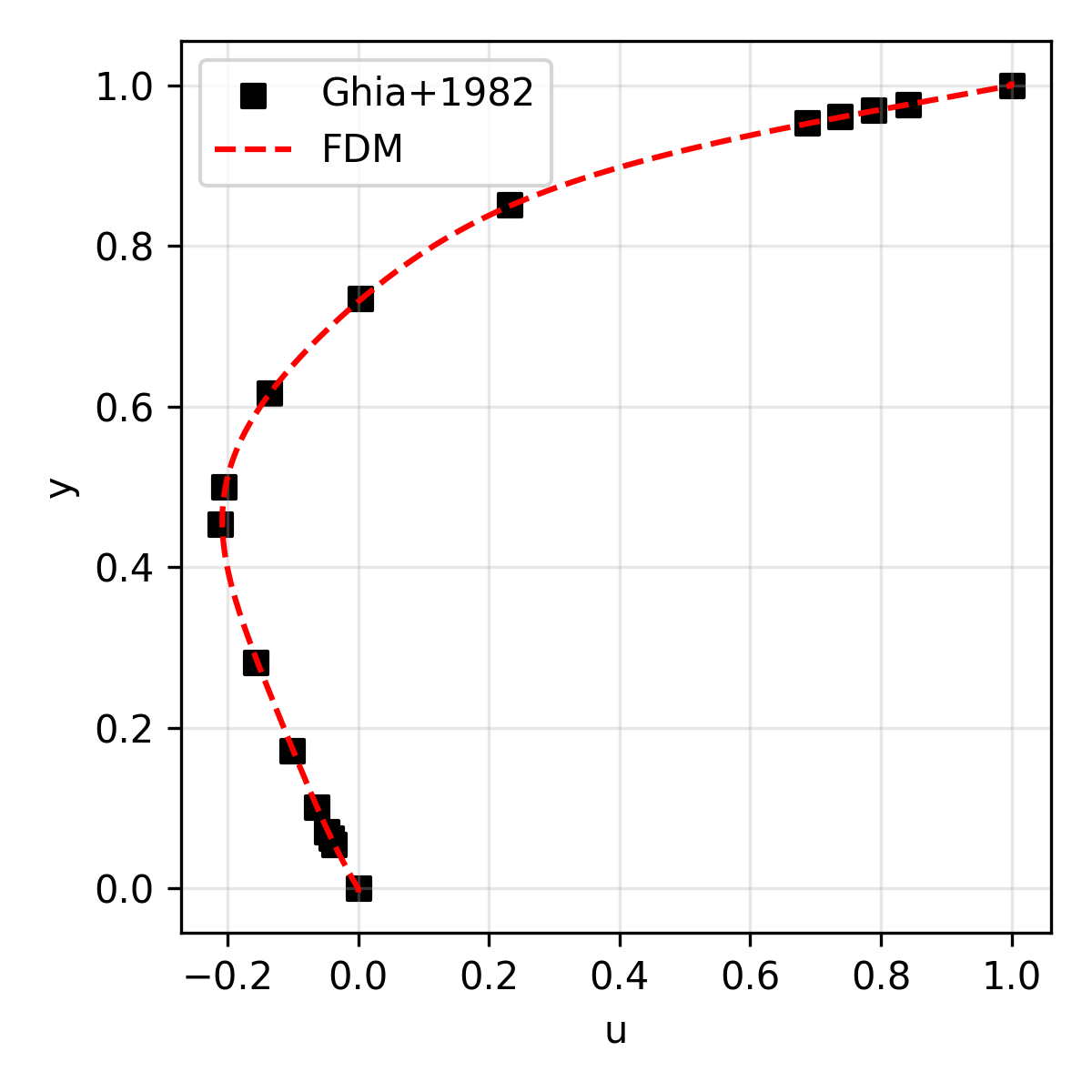 |
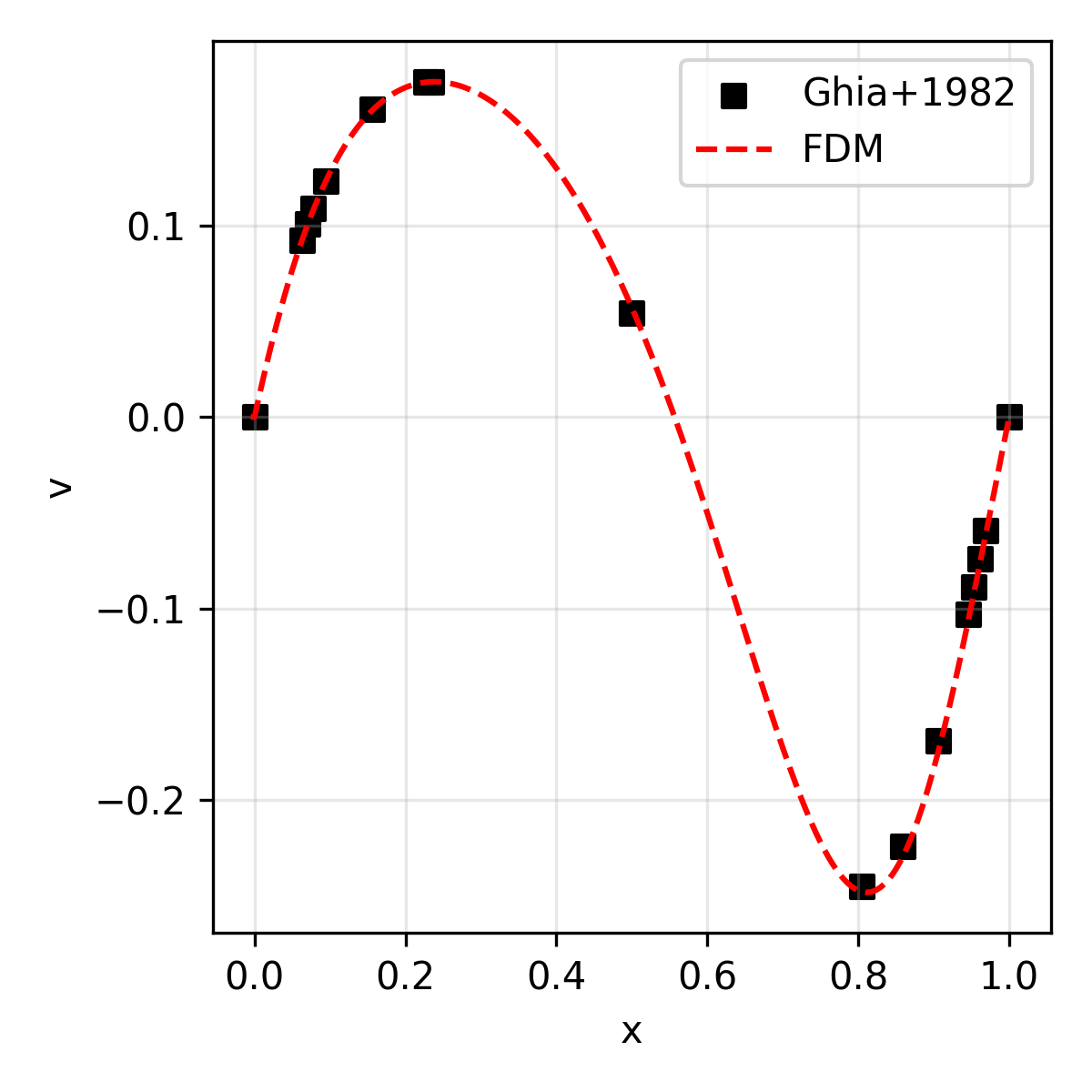 |
| 400 | 26.8 | 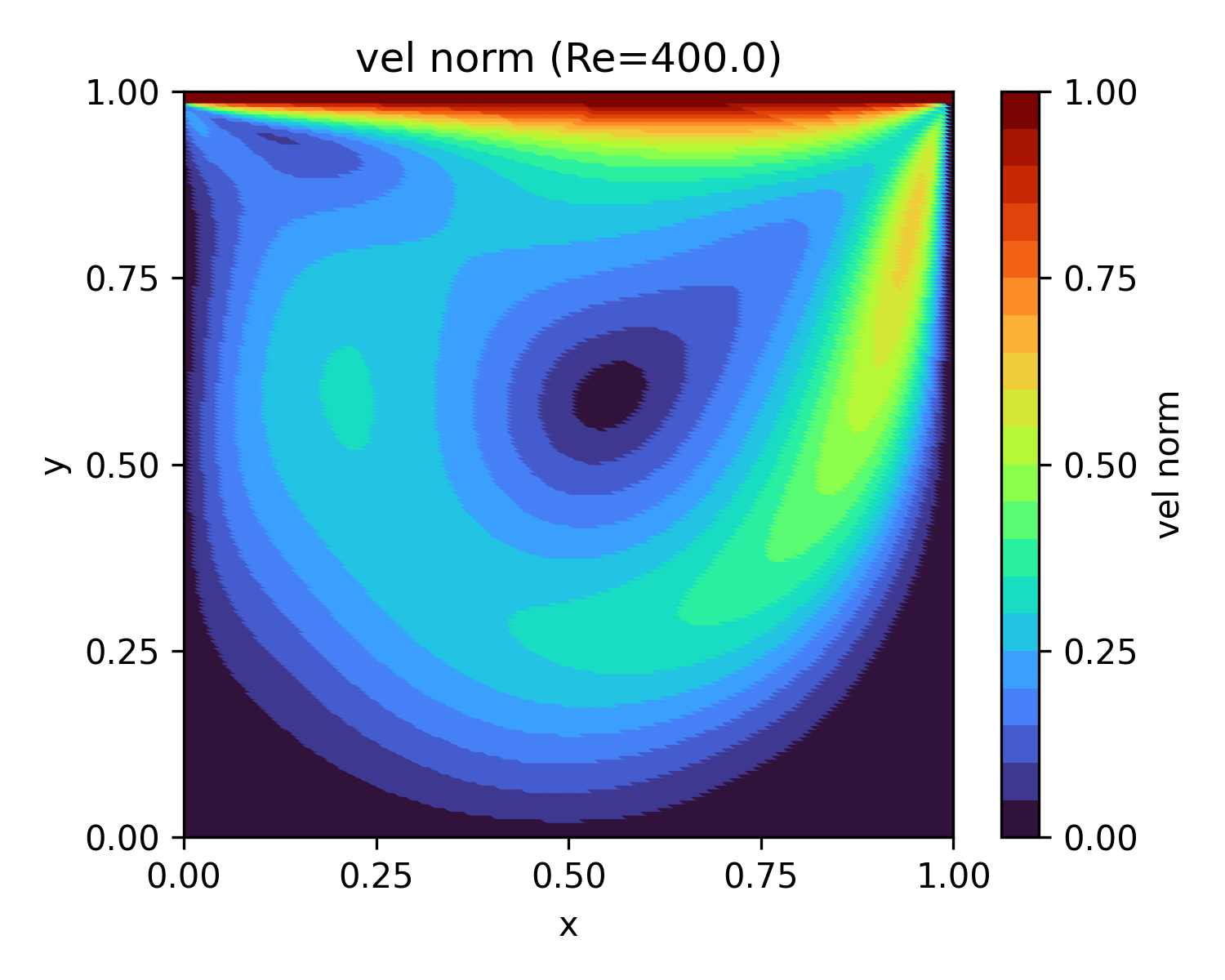 |
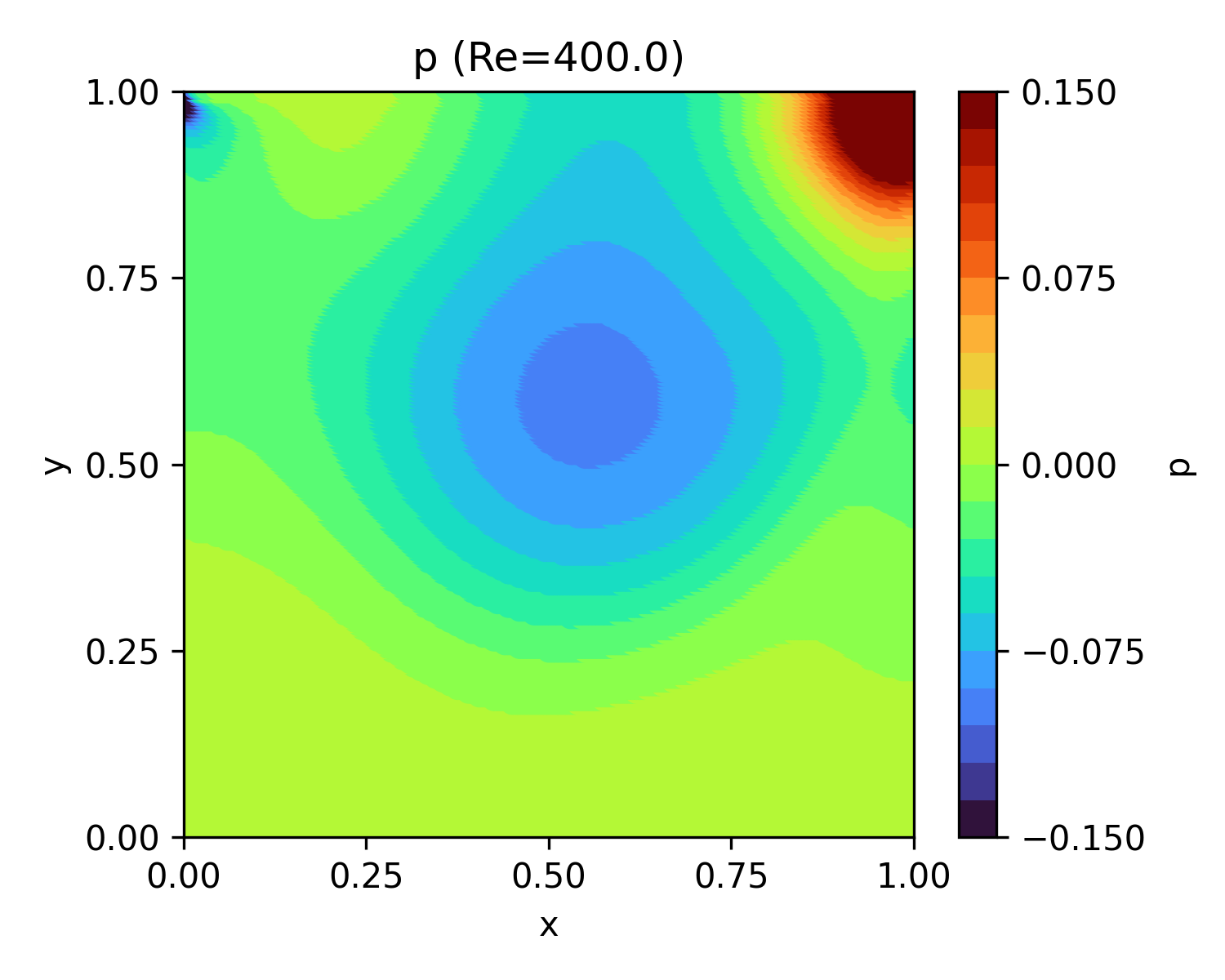 |
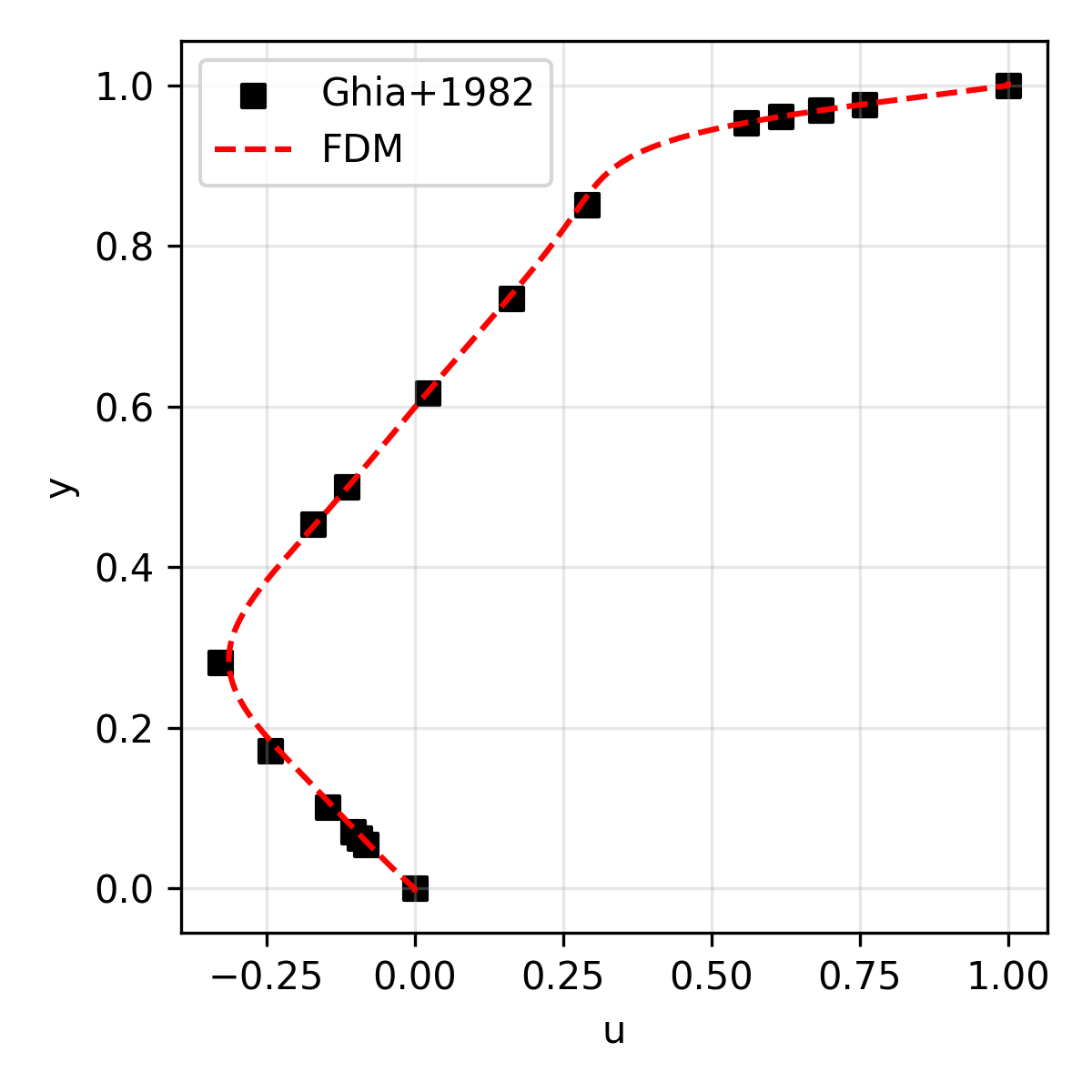 |
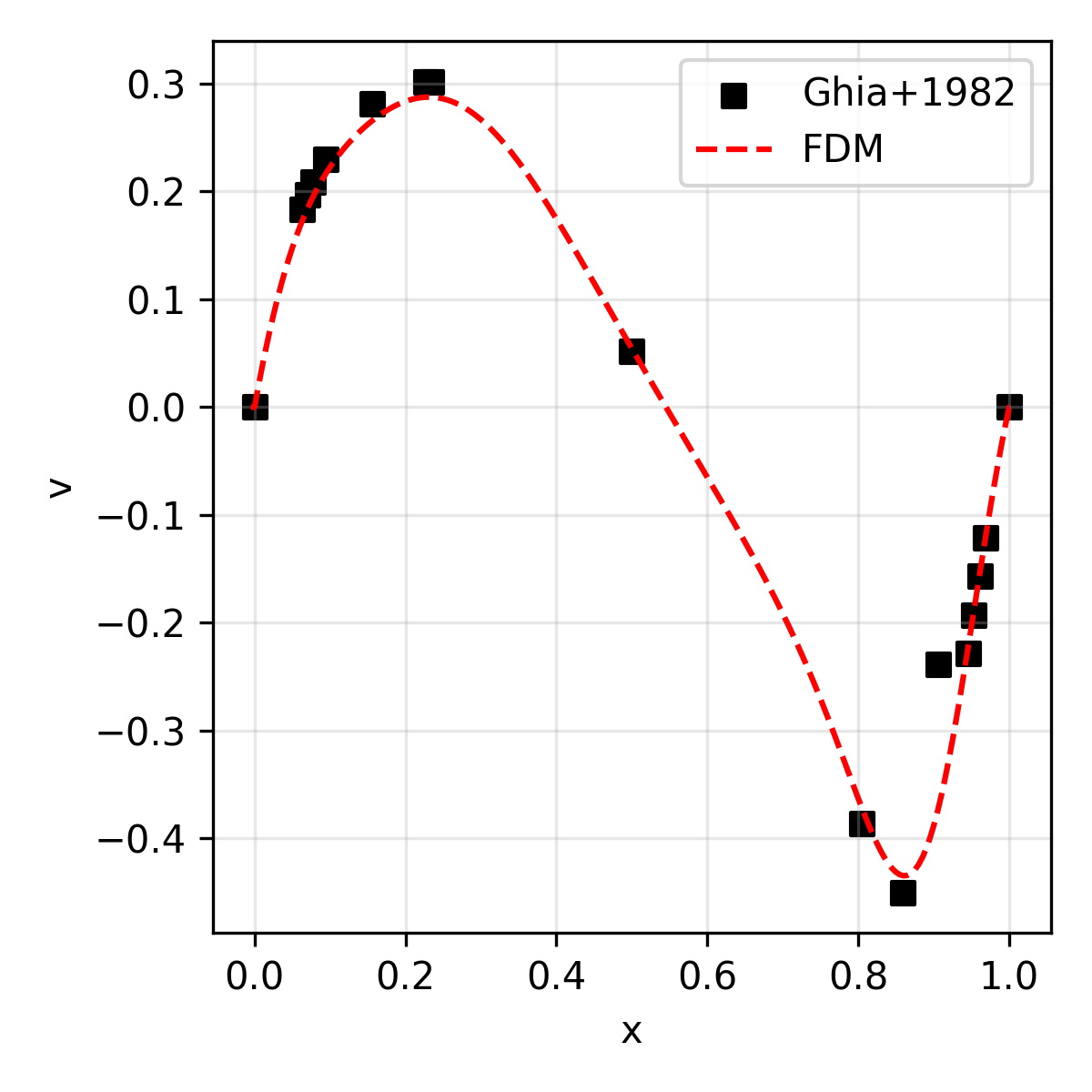 |
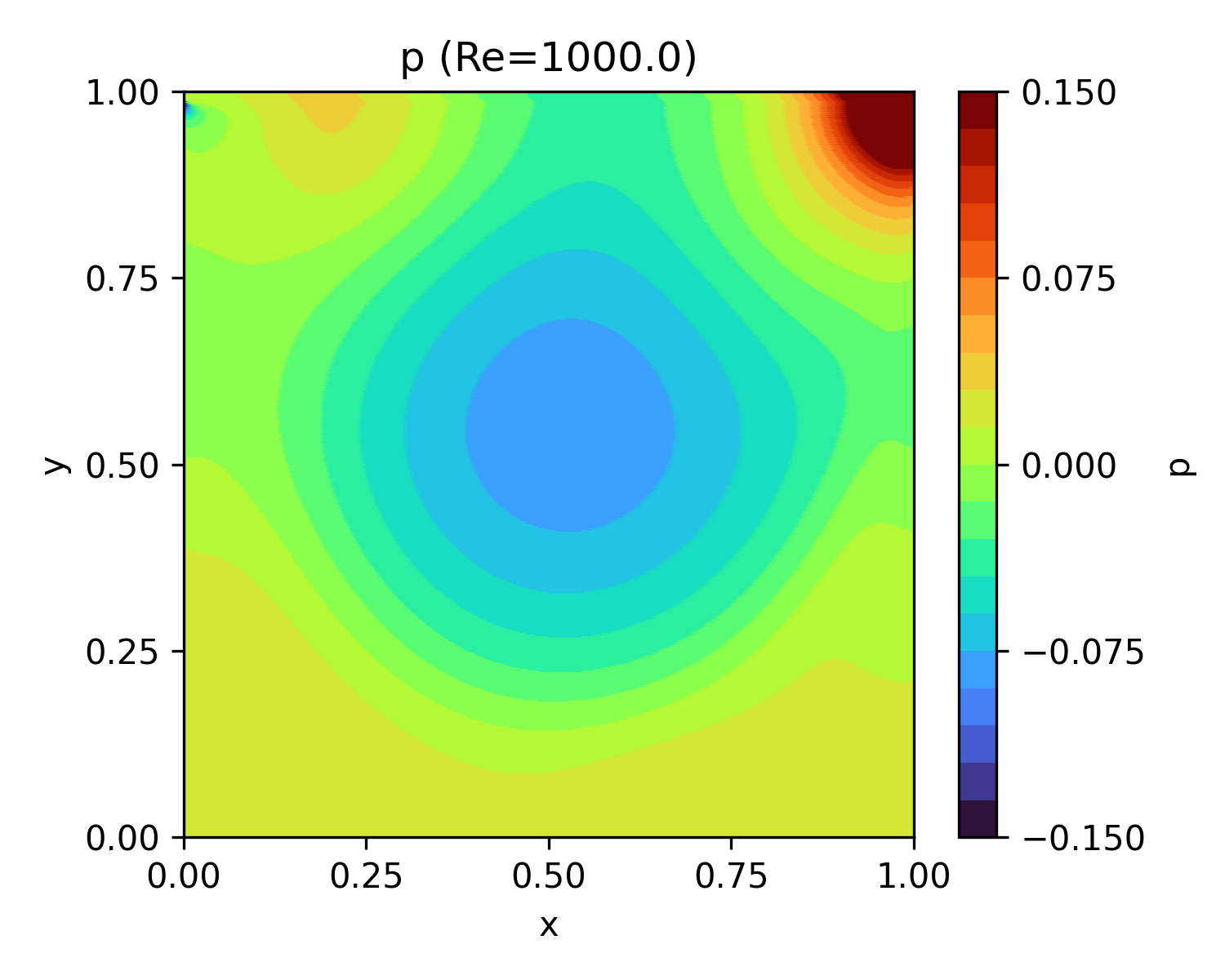
| 1,000 | 36.4 | 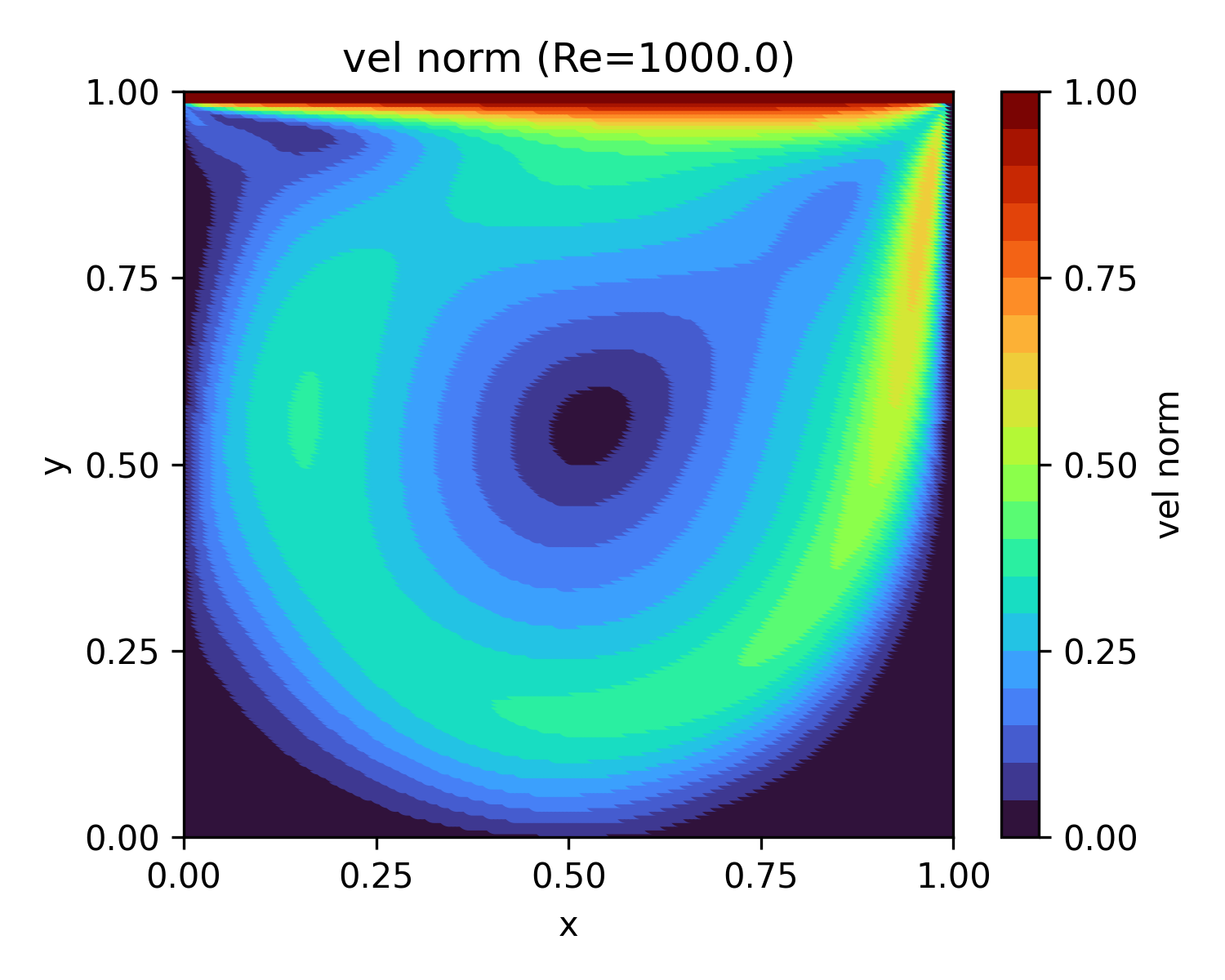 |
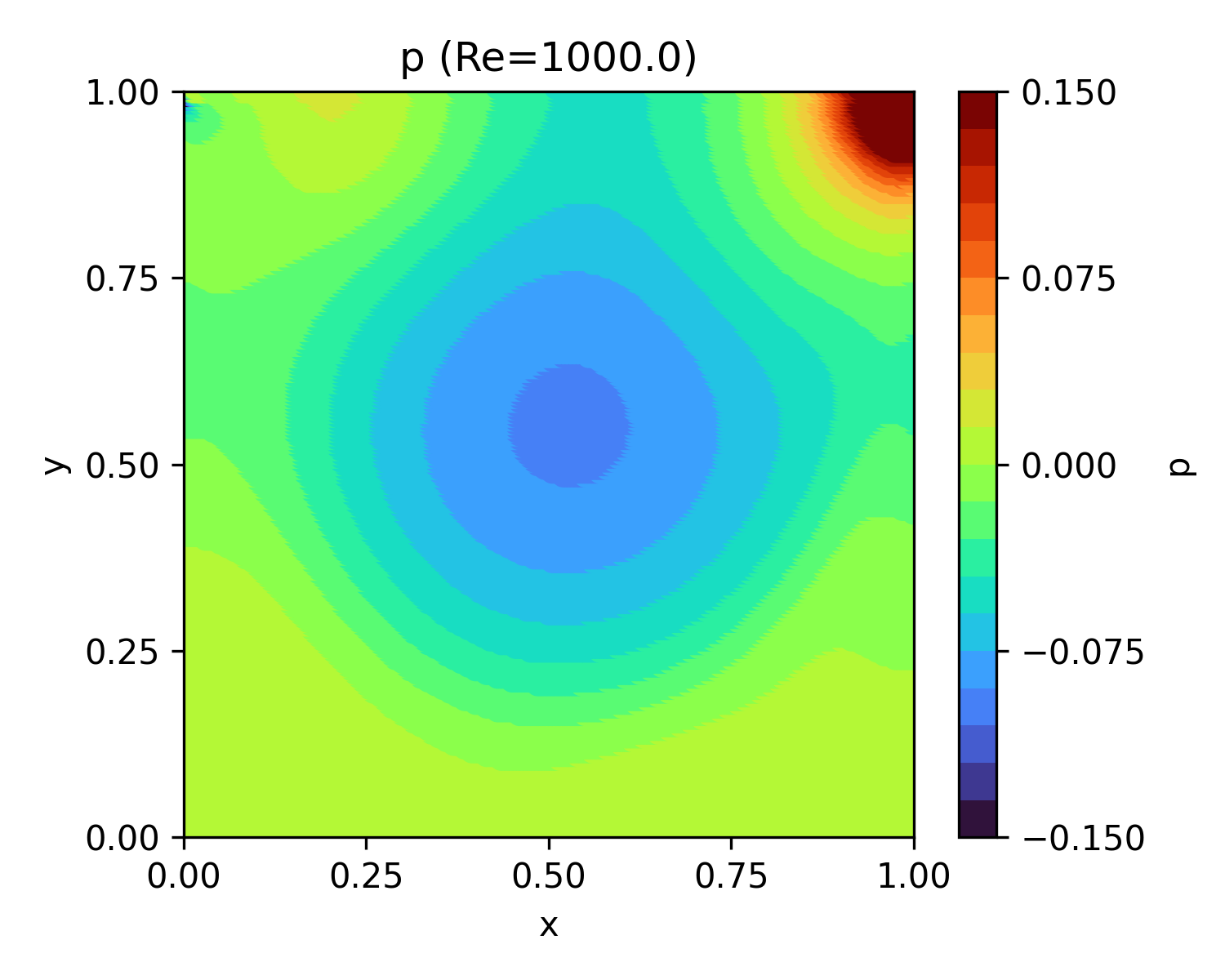 |
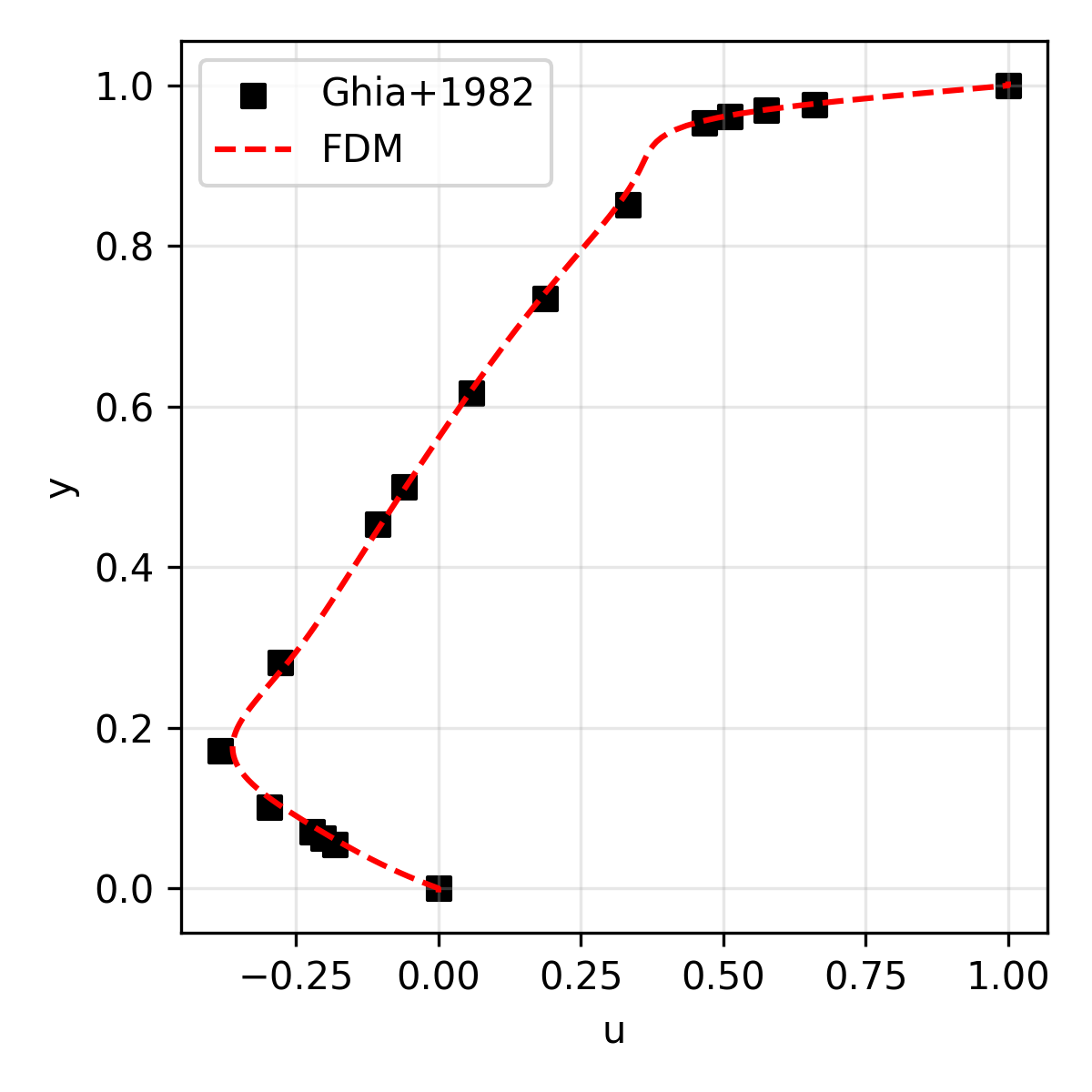 |
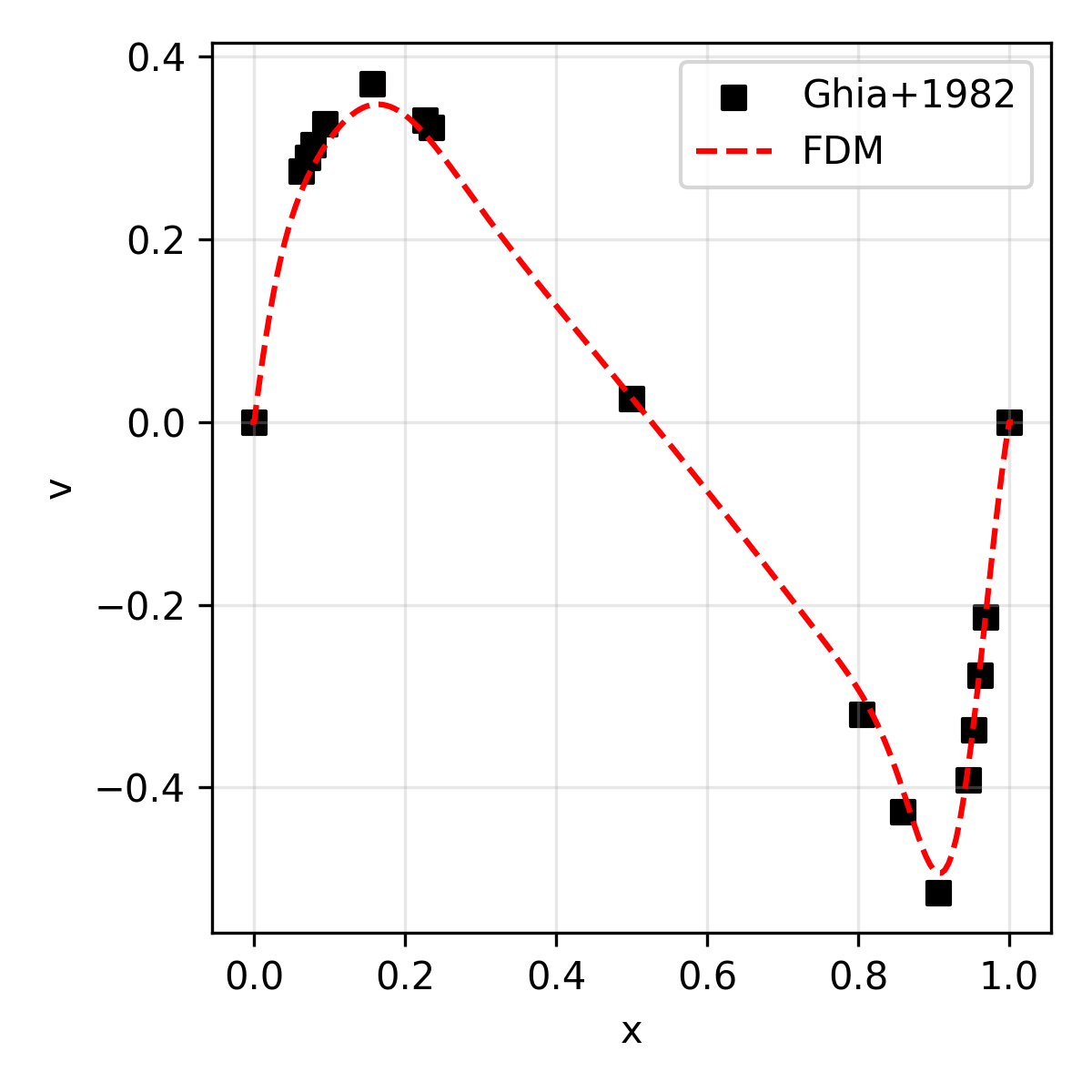 |
| 3,200 | 87.5 | 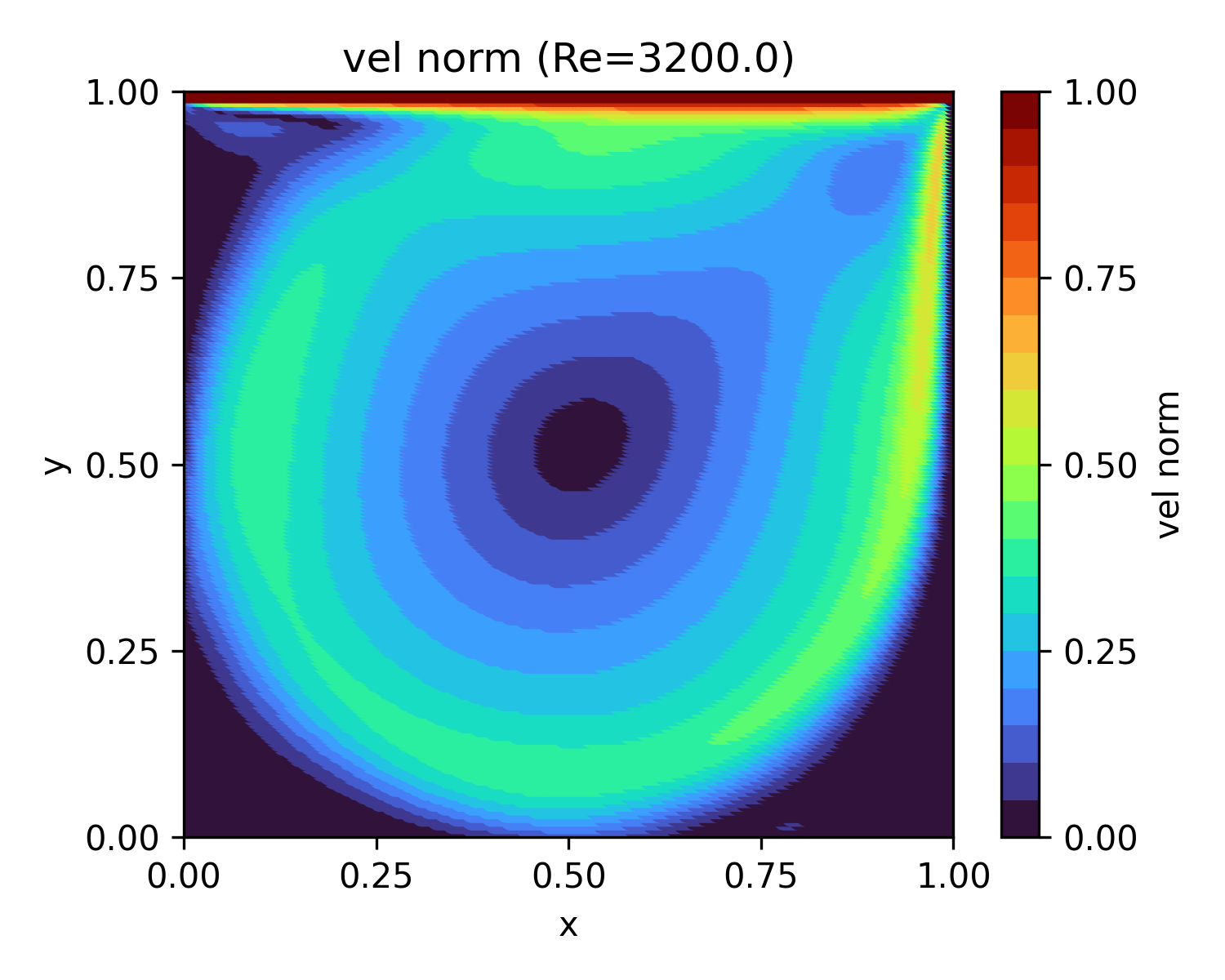 |
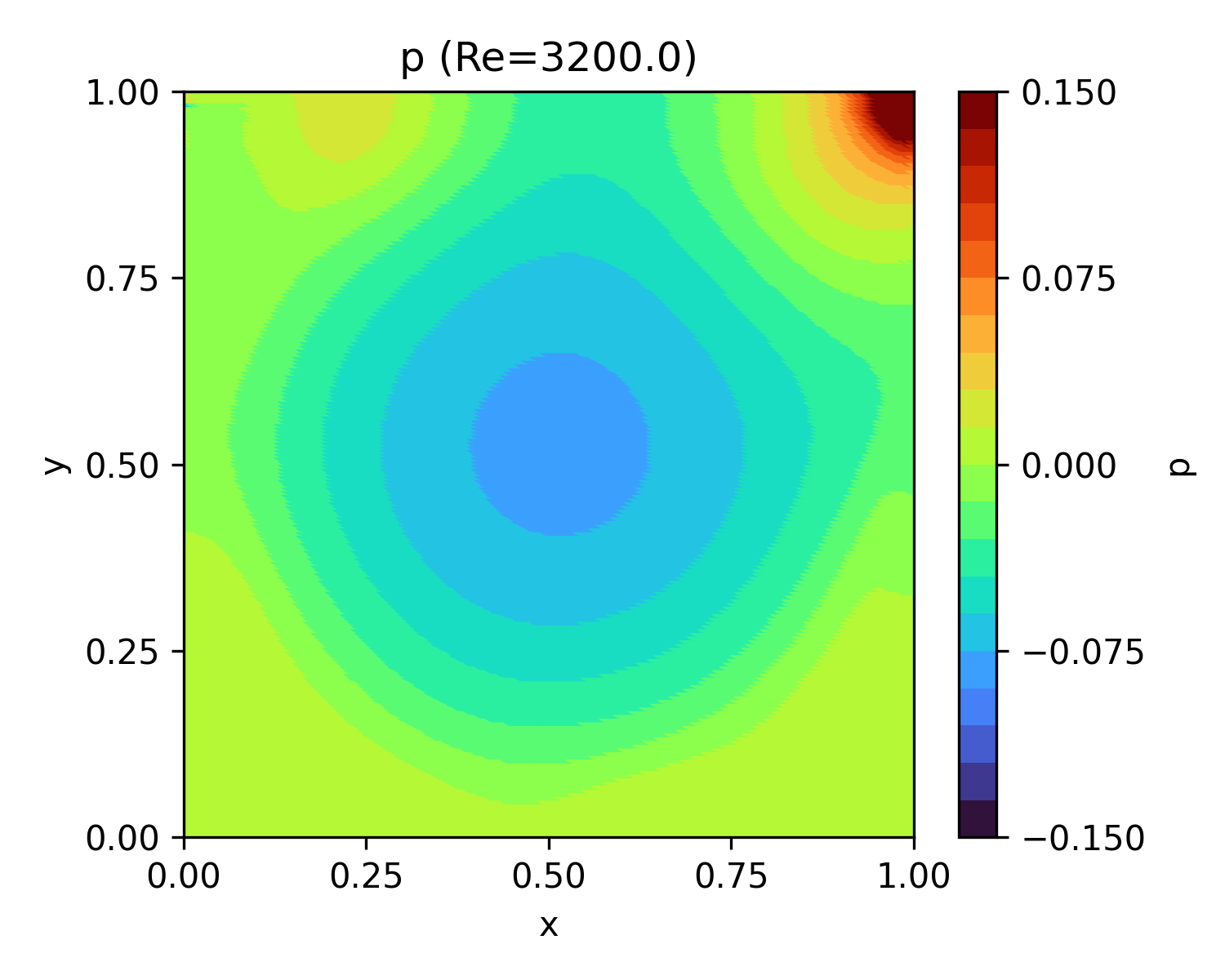 |
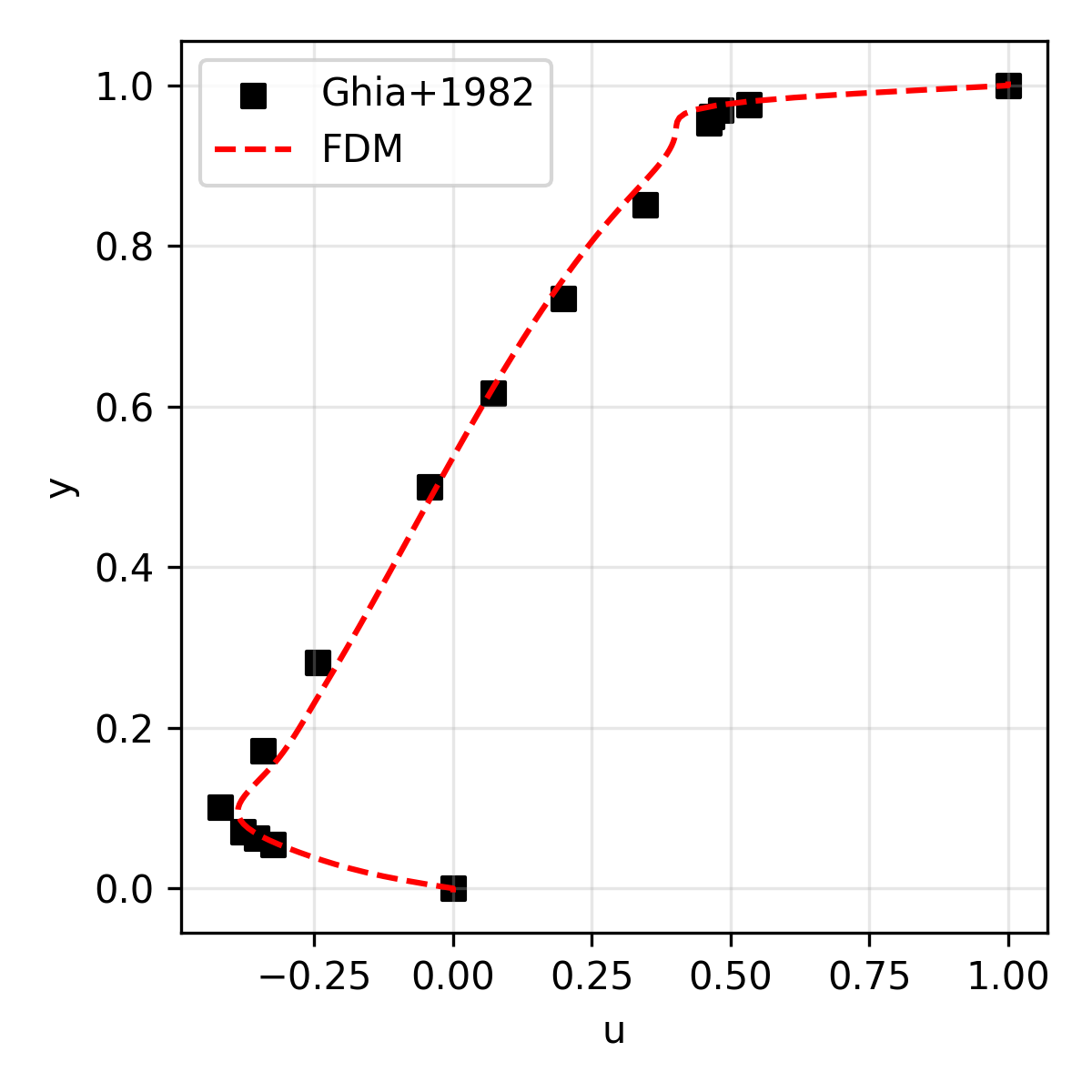 |
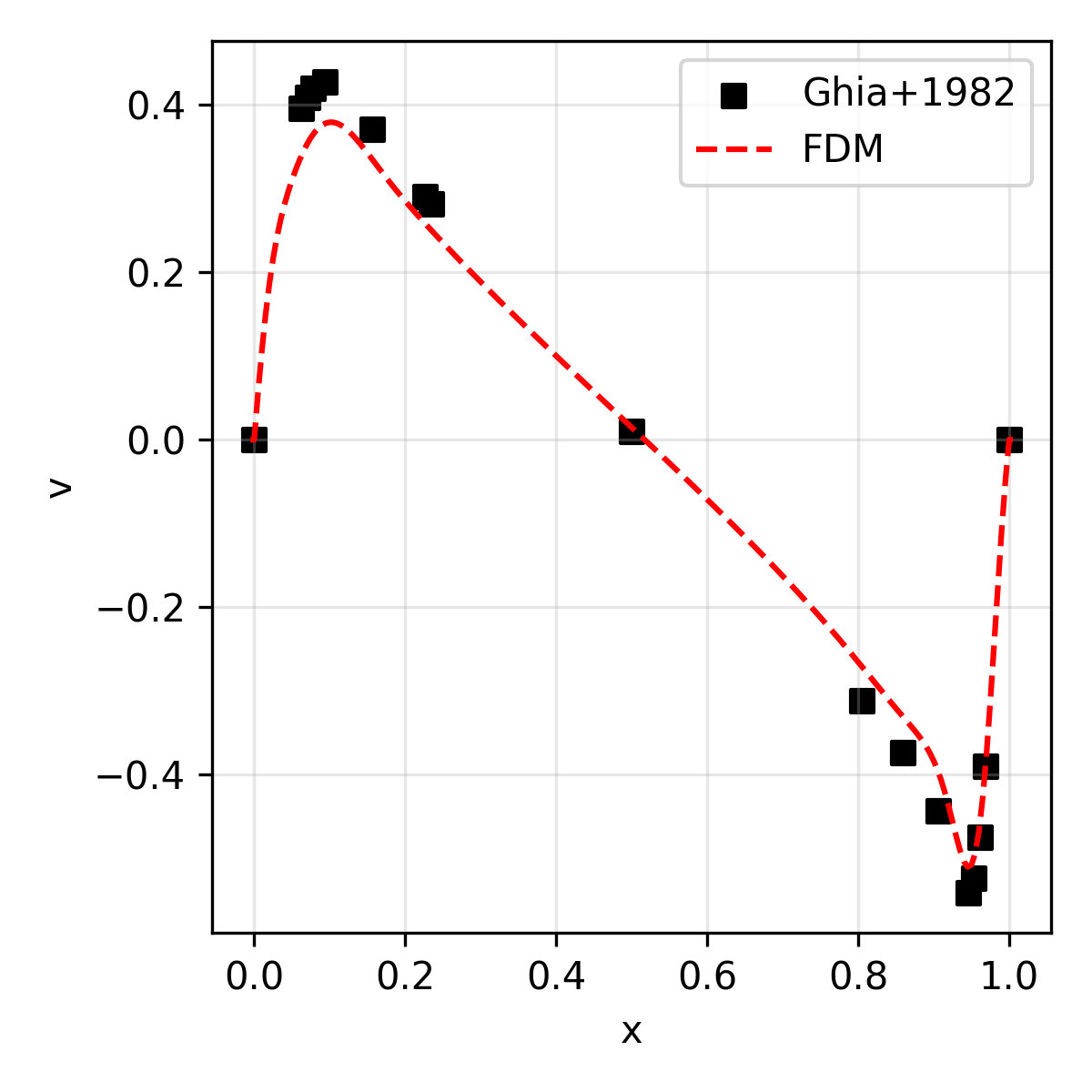 |
| 5,000 | 148.5 | 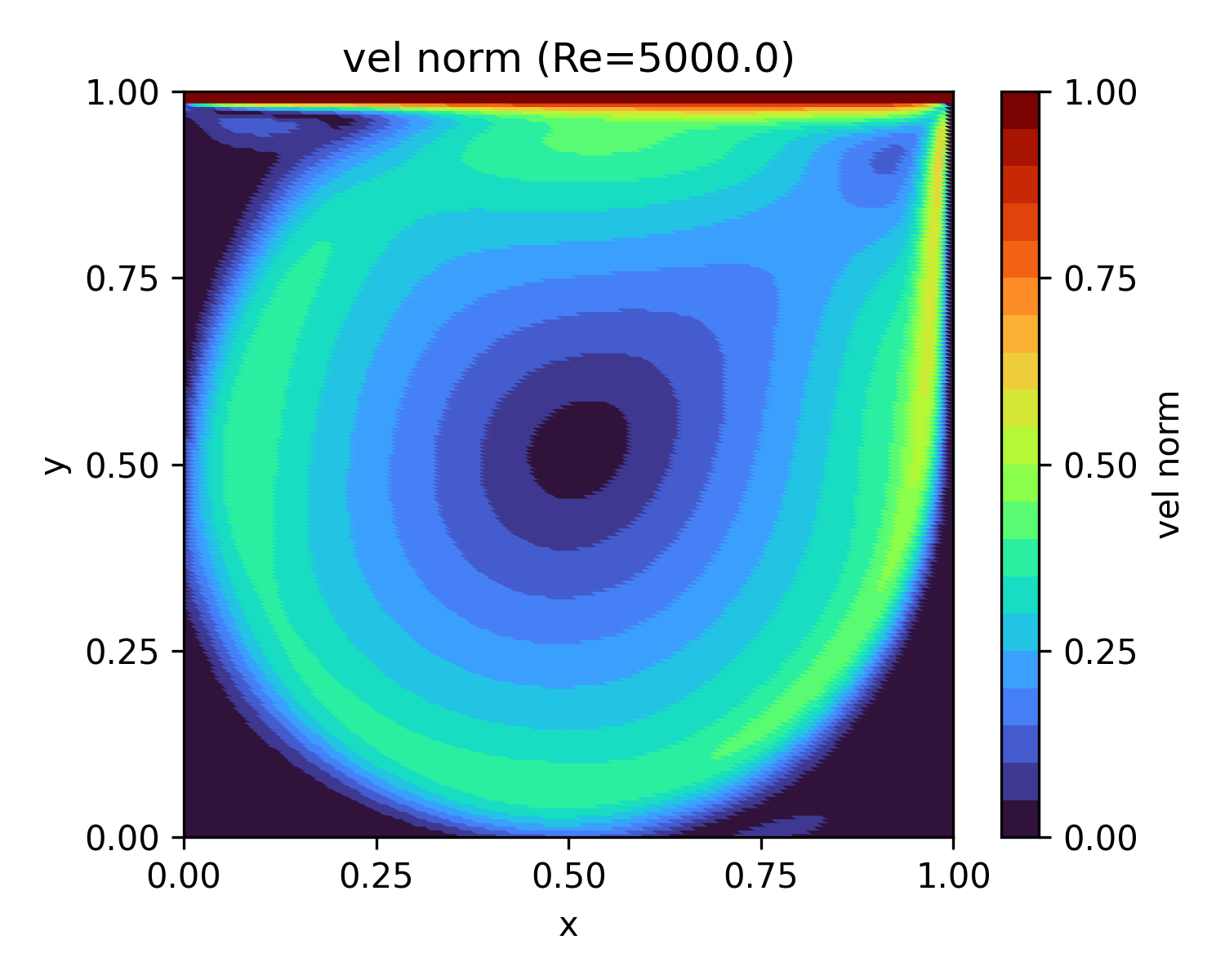 |
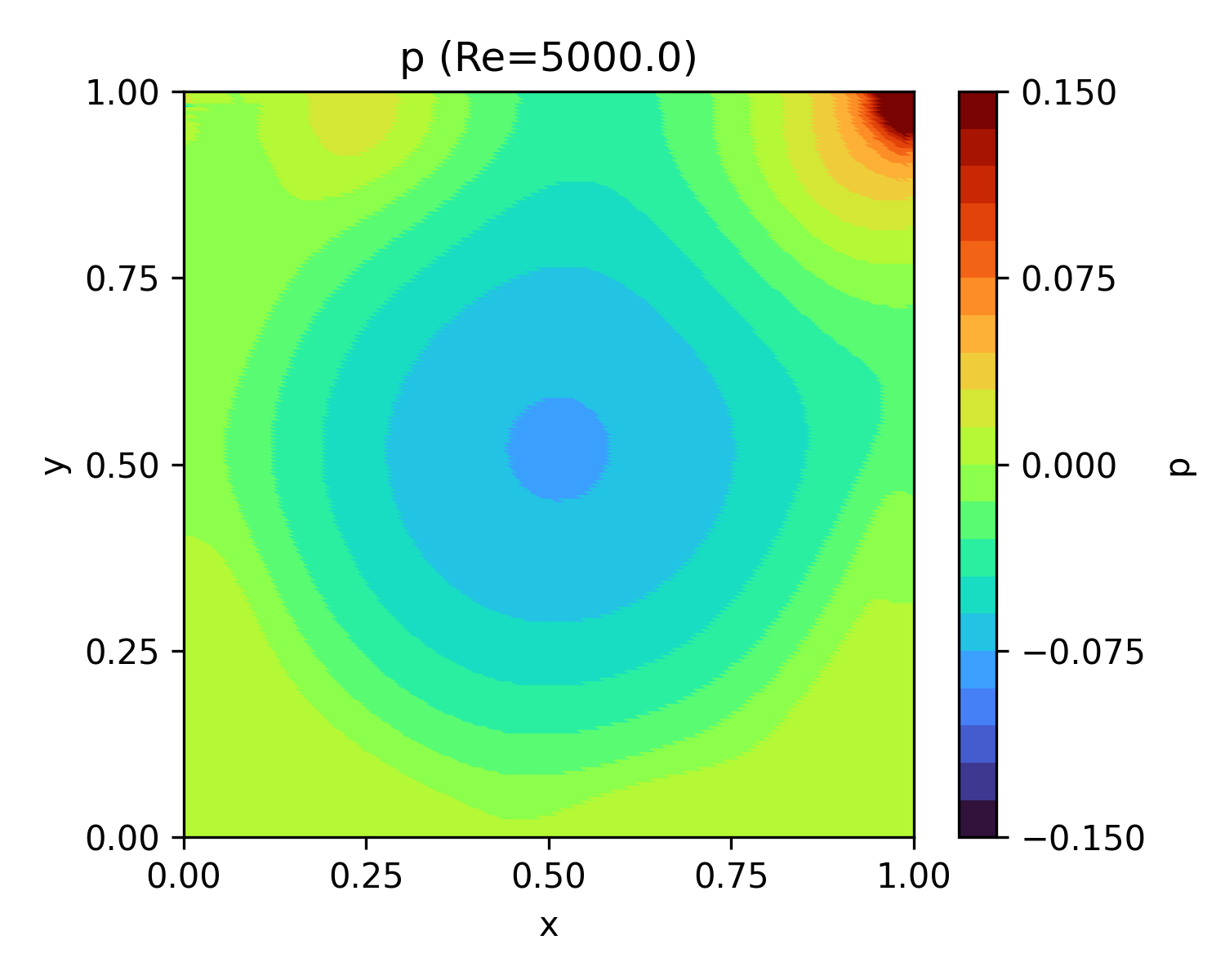 |
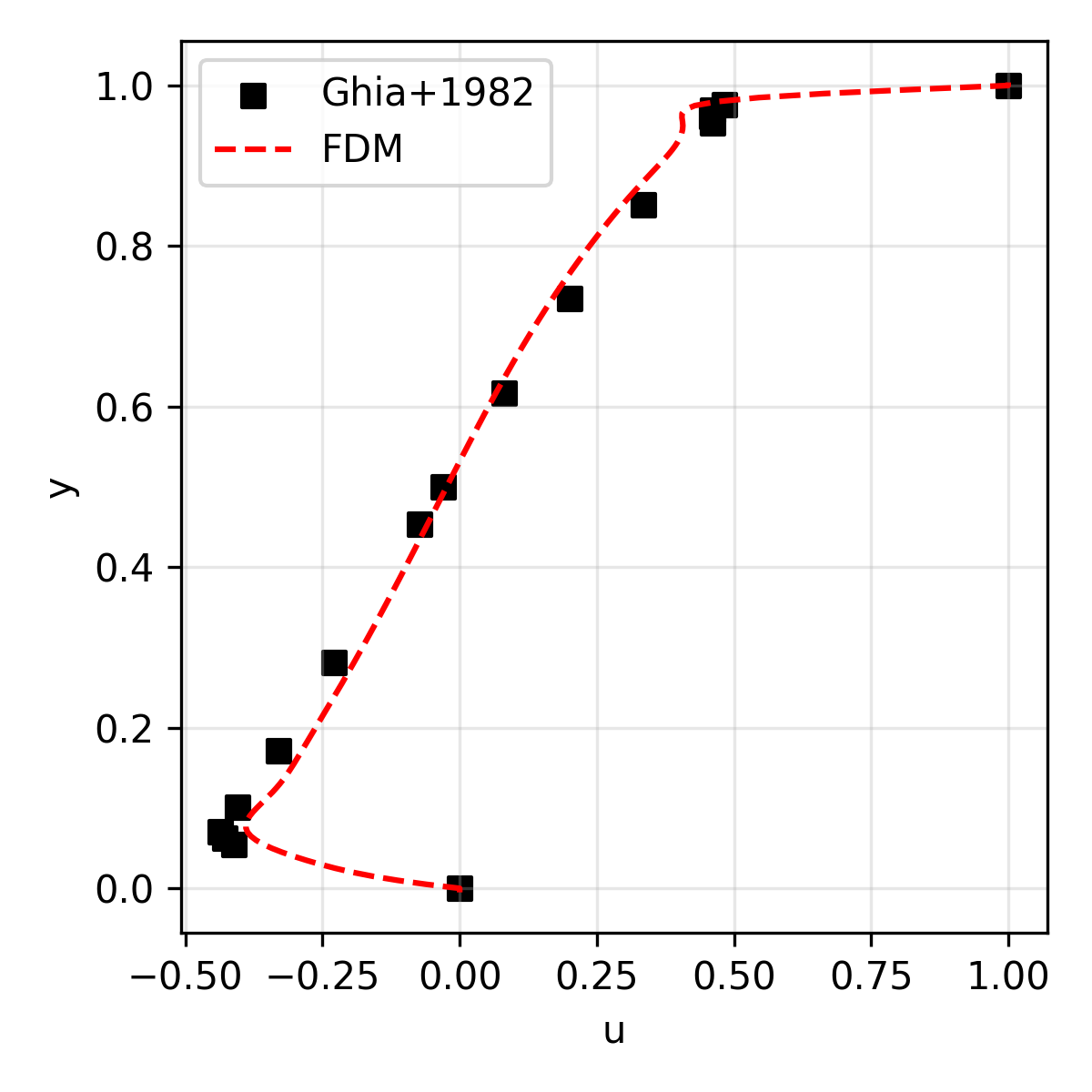 |
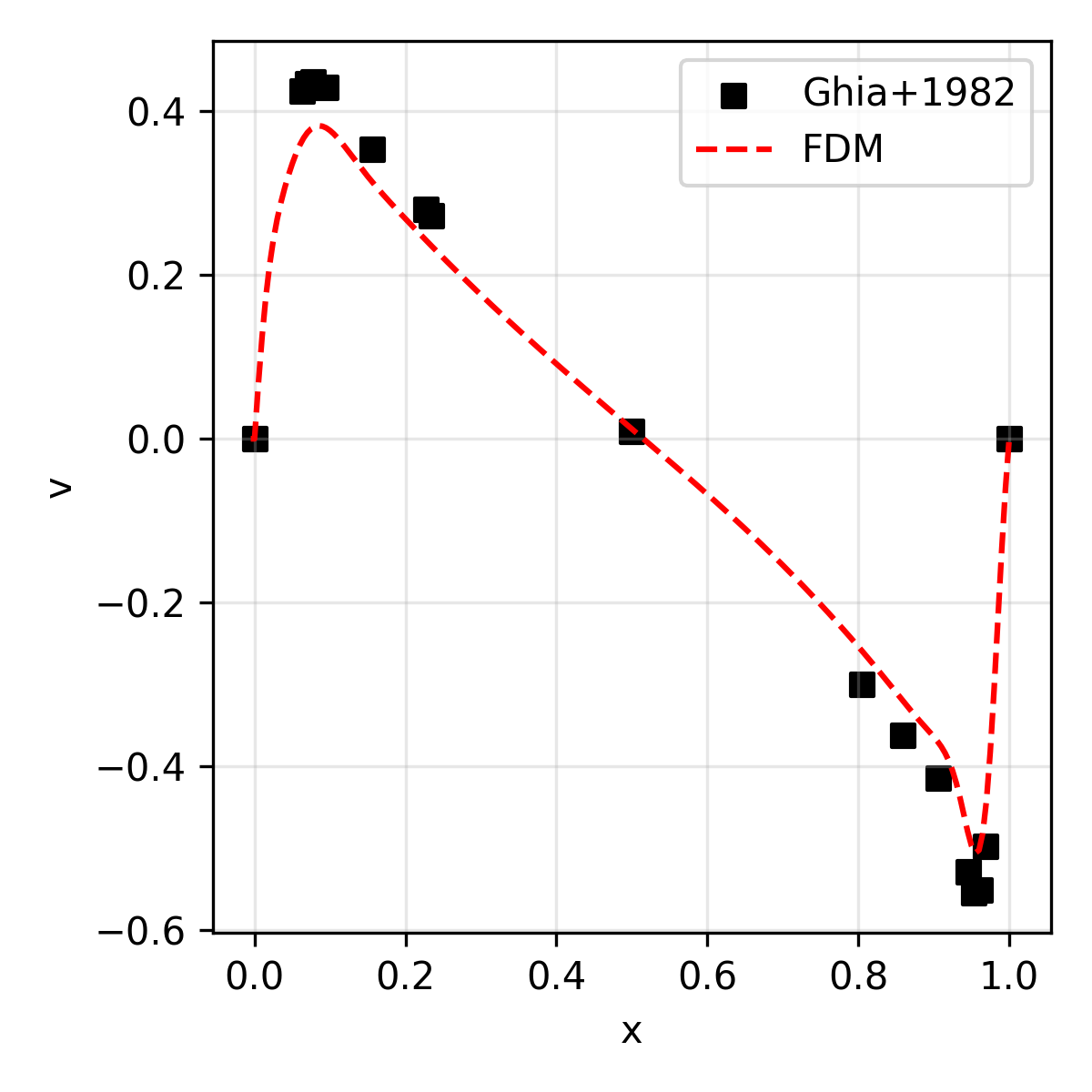 |
| Re | t | Velocity norm | Pressure | u | v |
|---|---|---|---|---|---|
| 100 | 13.7 | 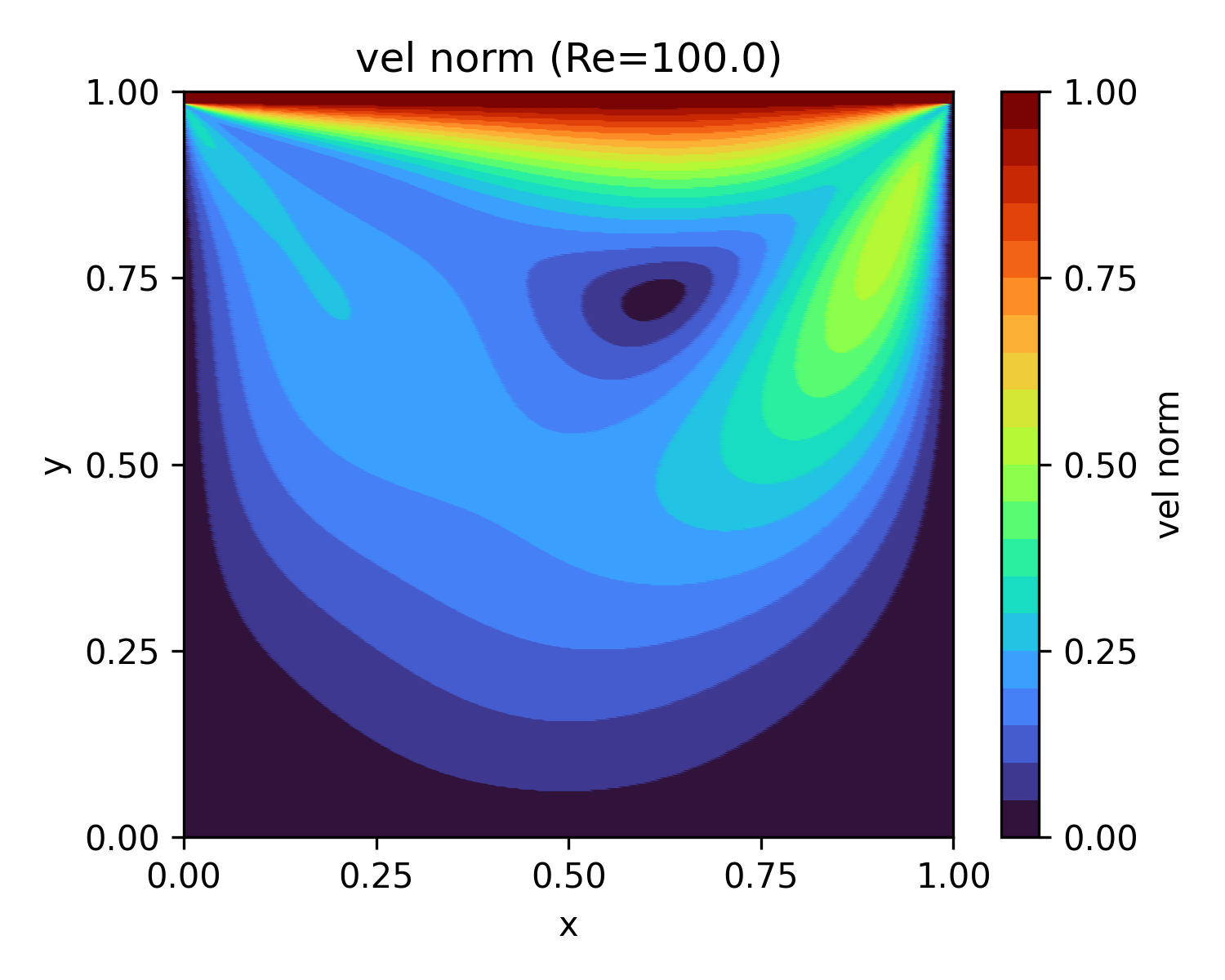 |
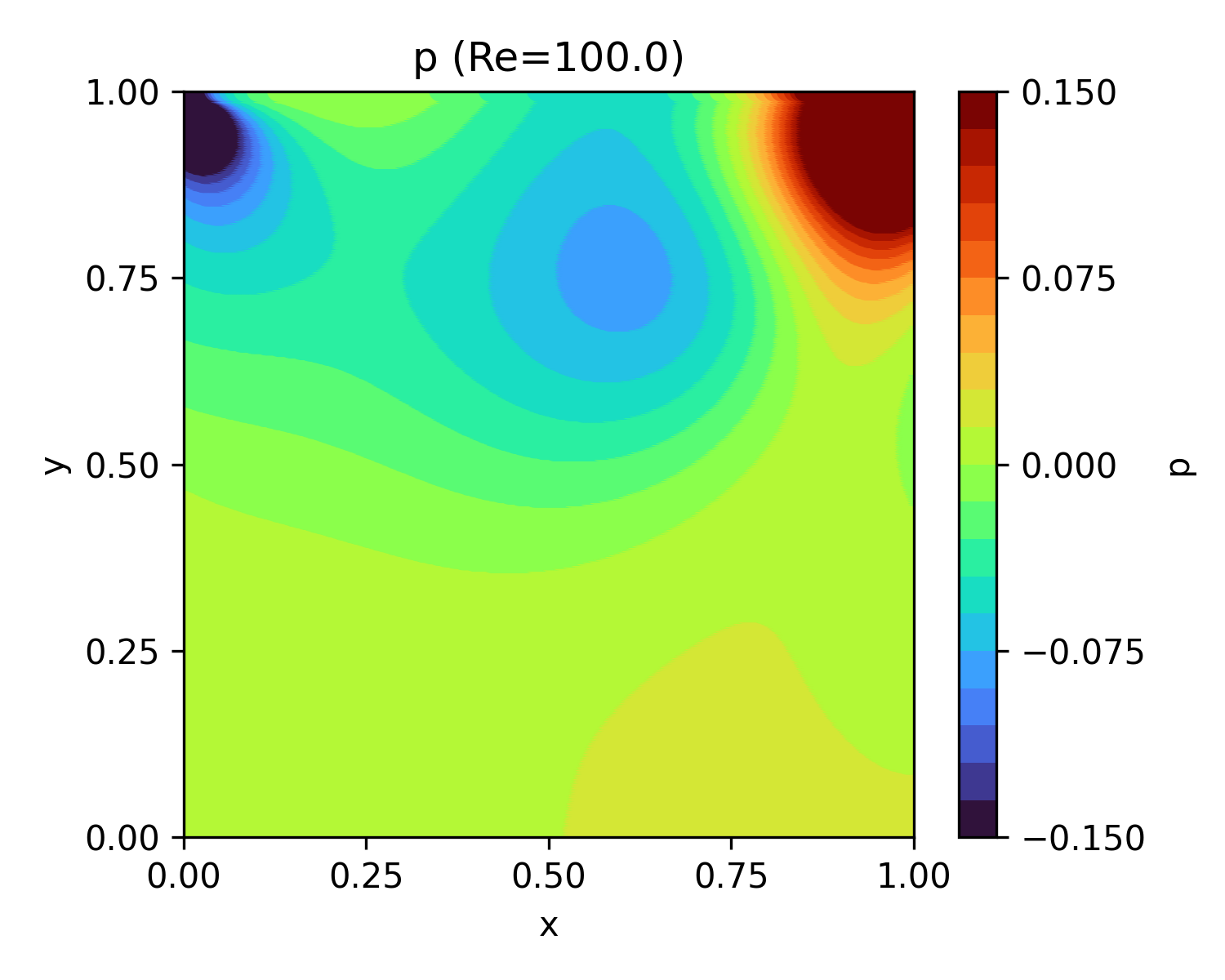 |
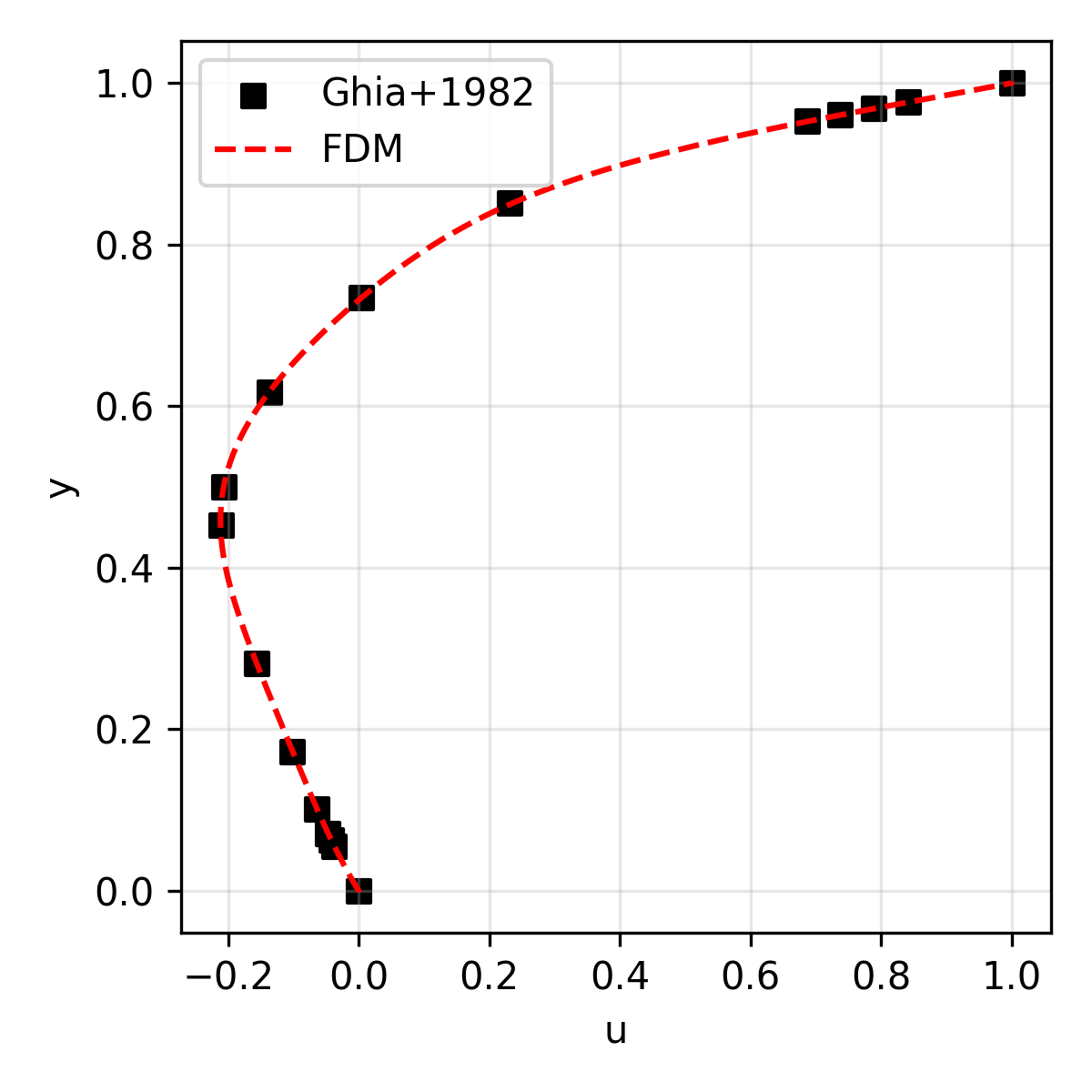 |
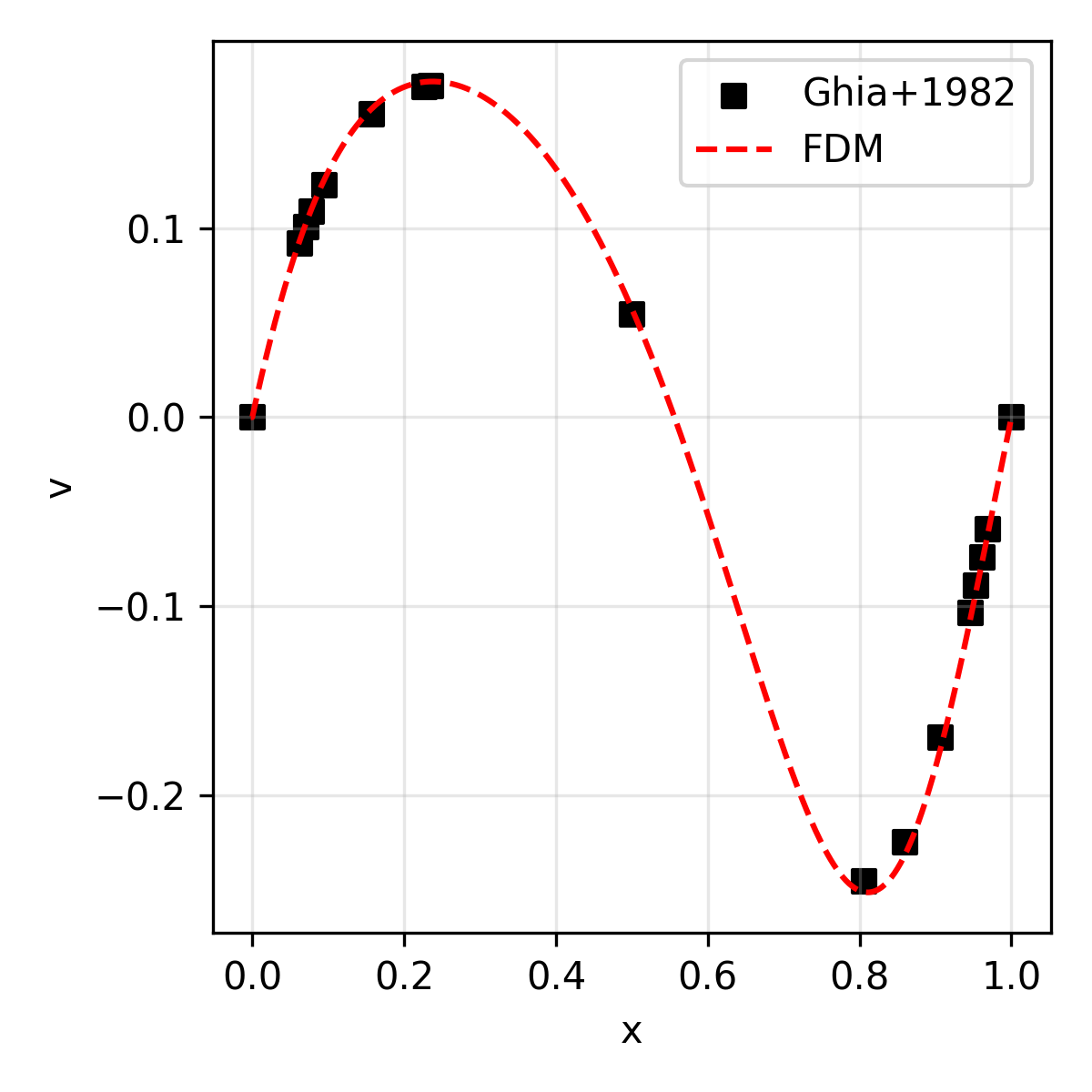 |
| 400 | 19.2 | 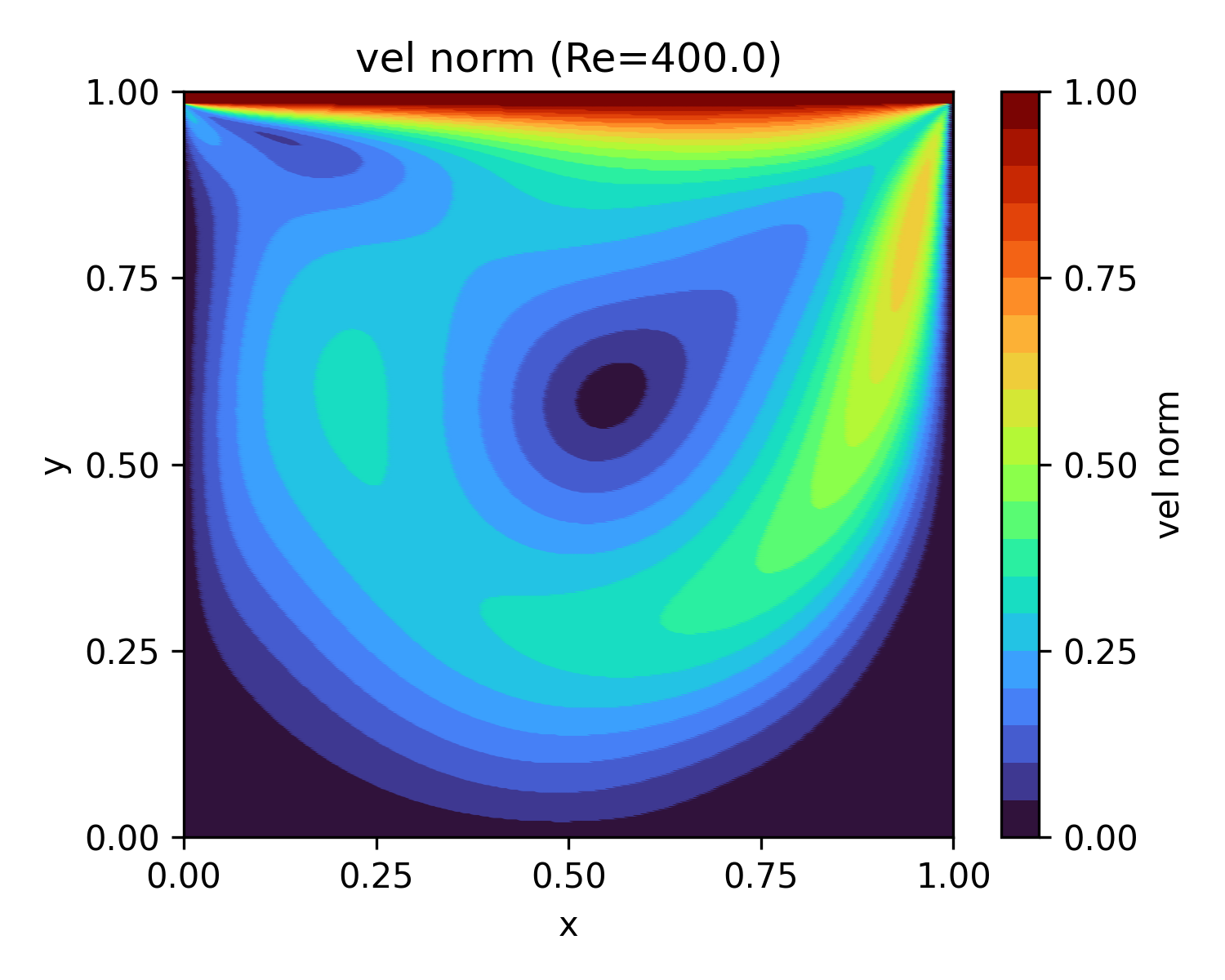 |
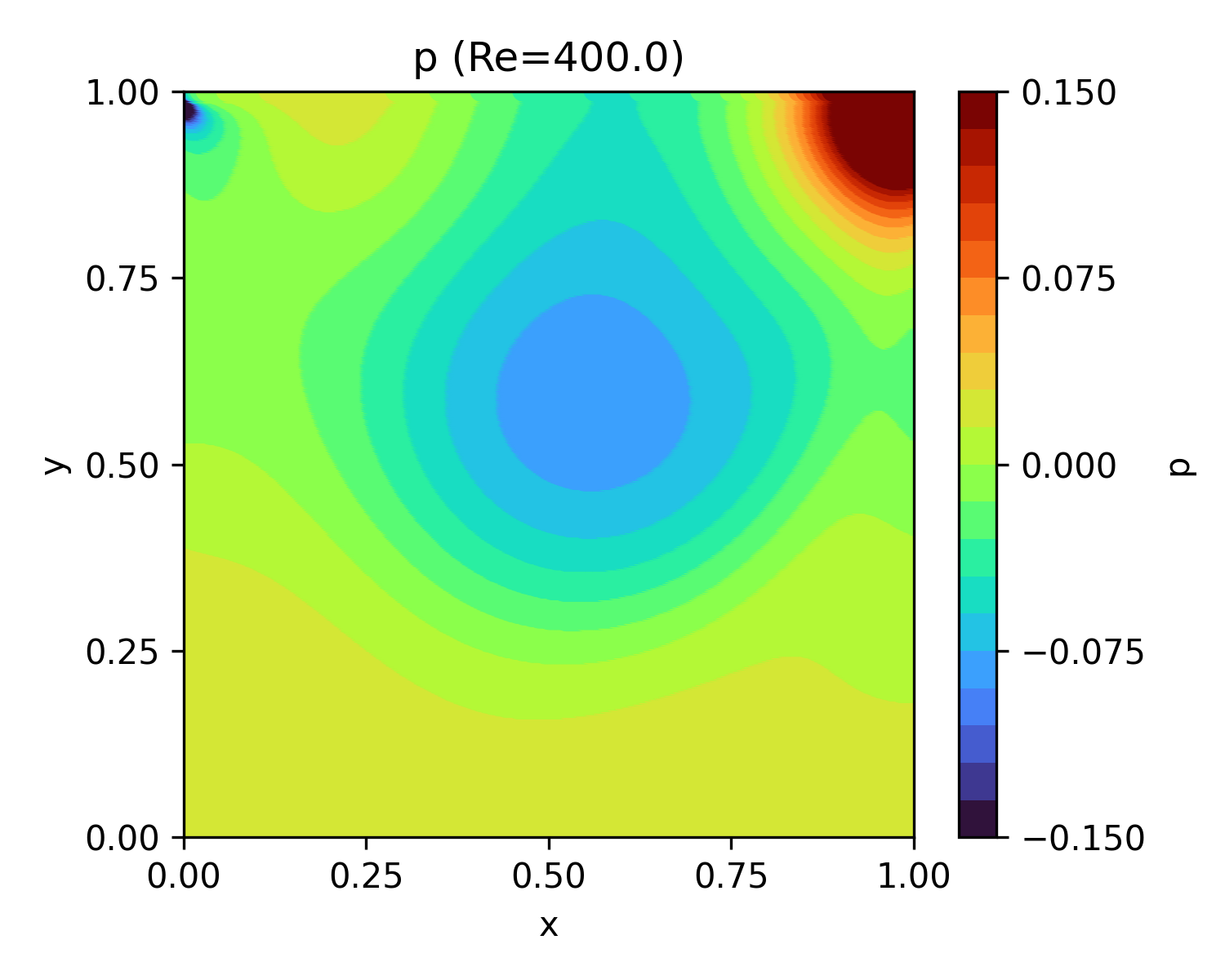 |
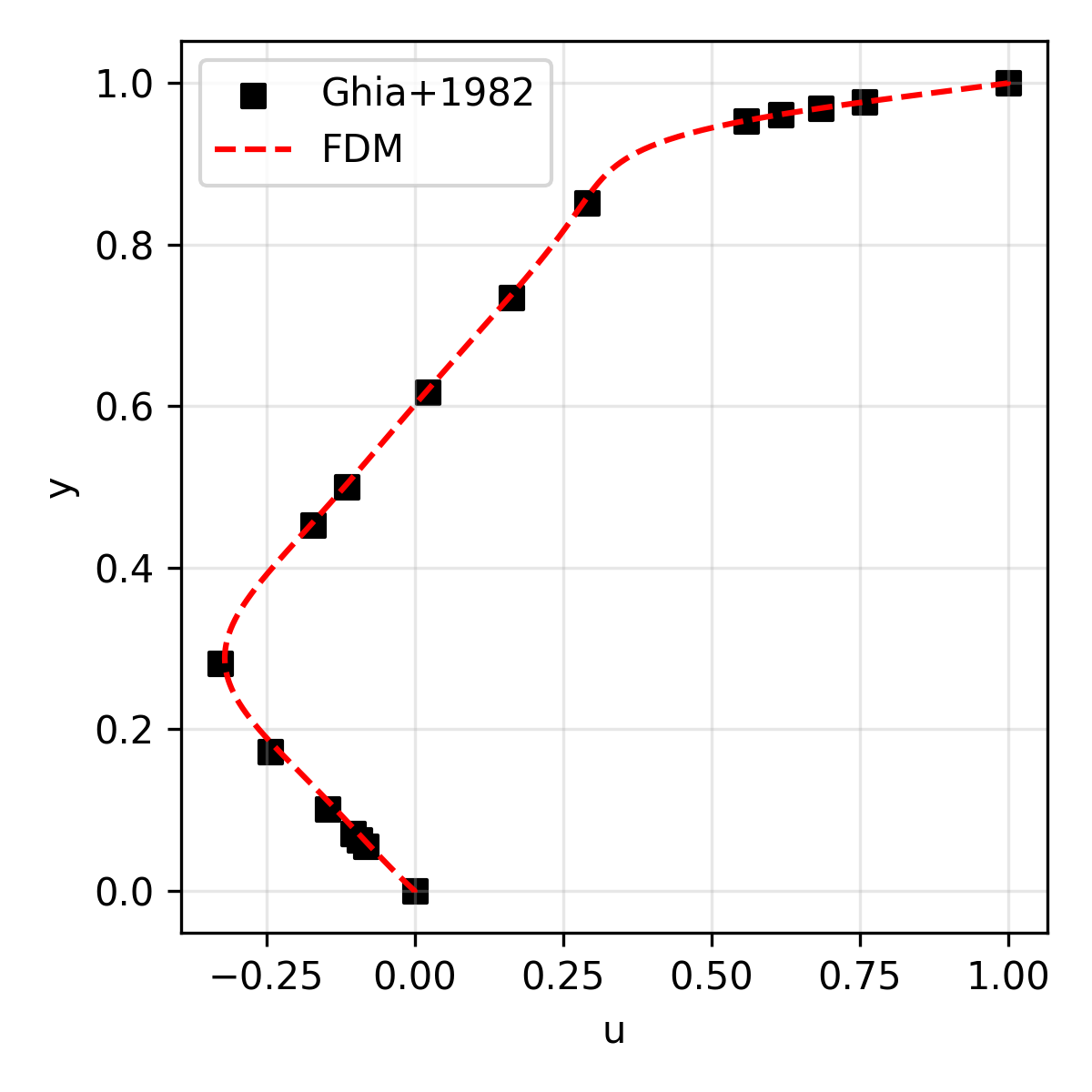 |
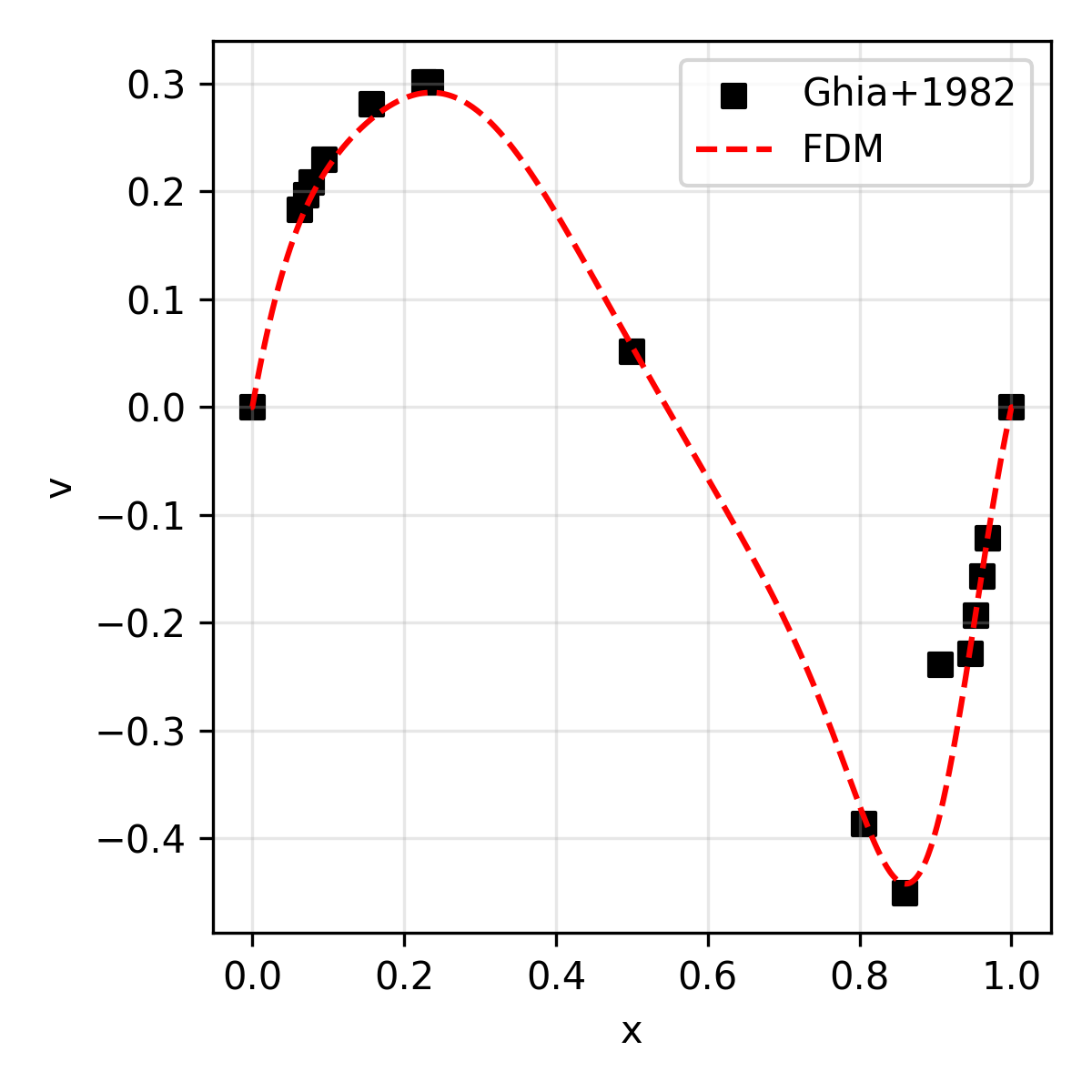 |
| 1,000 | 30.7 | 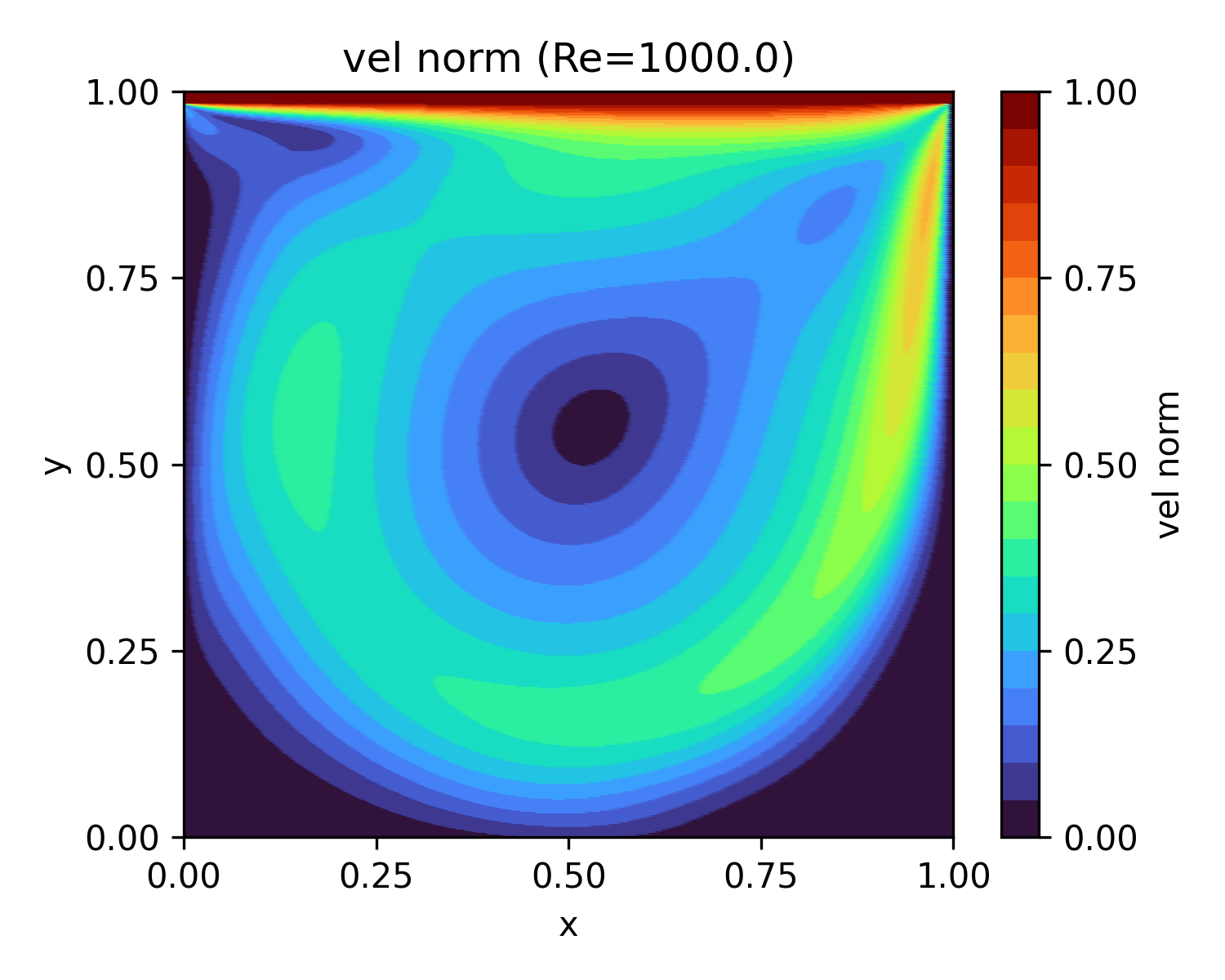 |
 |
 |
 |
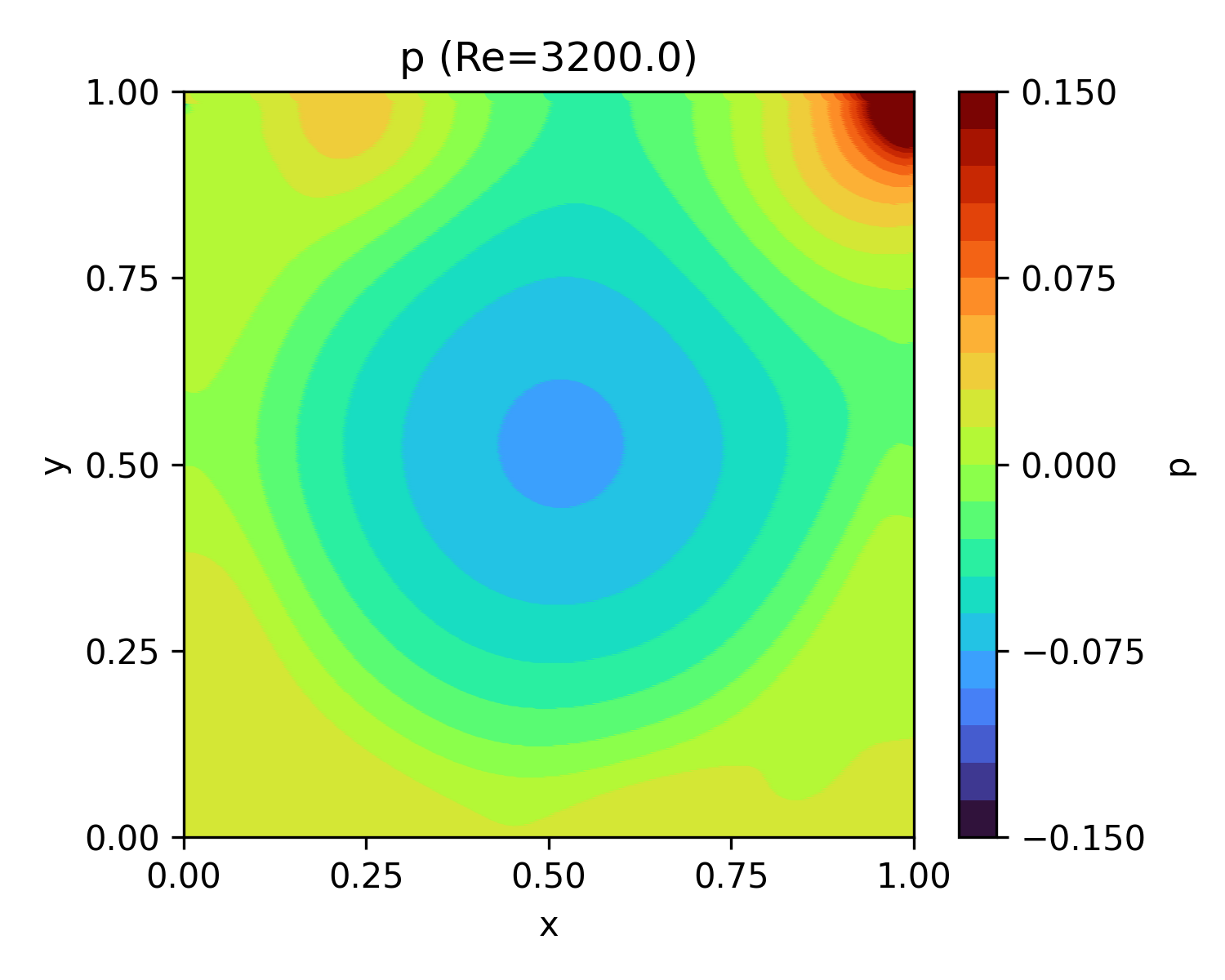
| 3,200 | 68.4 | 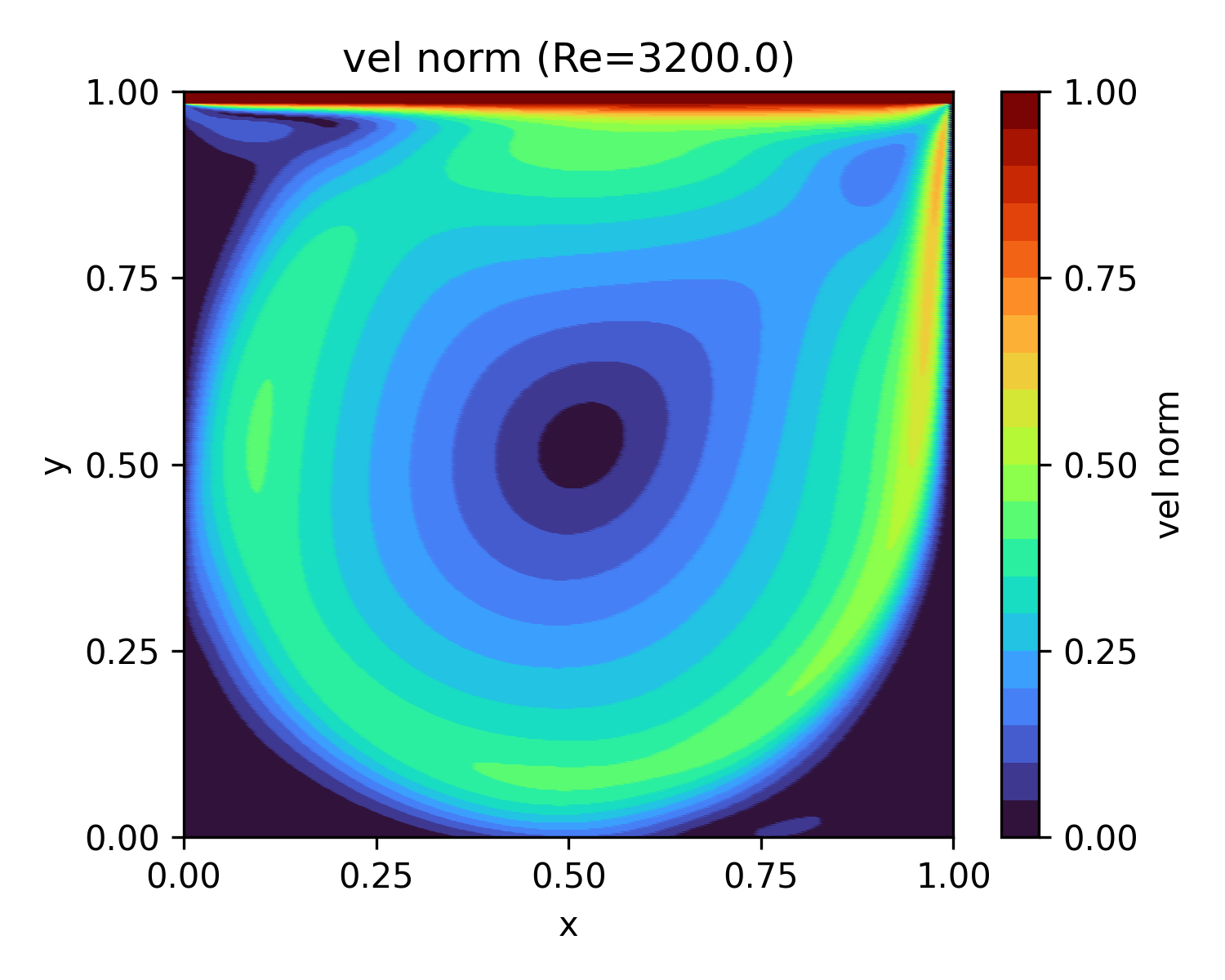 |
 |
 |
 |
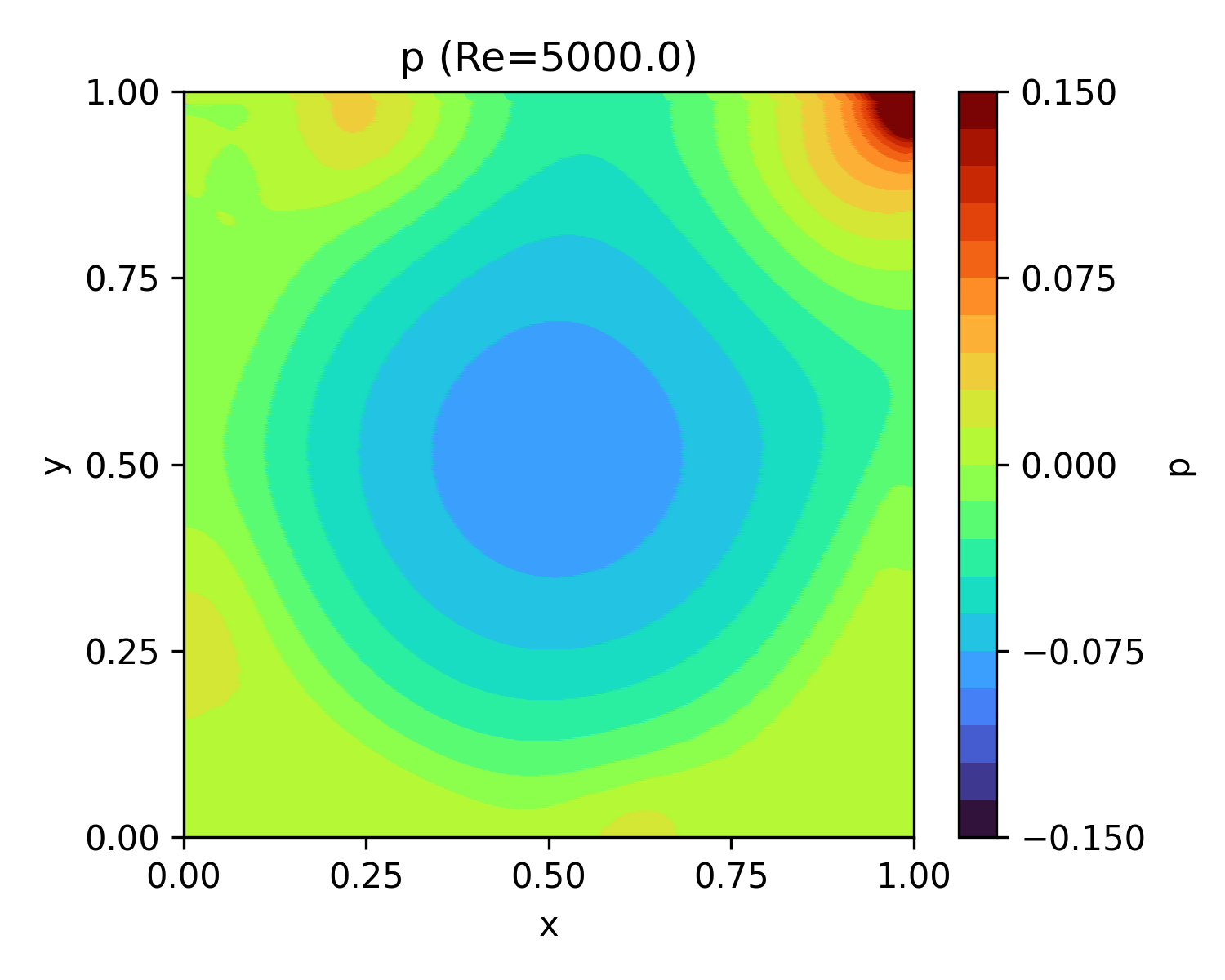
| 5,000 | 134.1 | 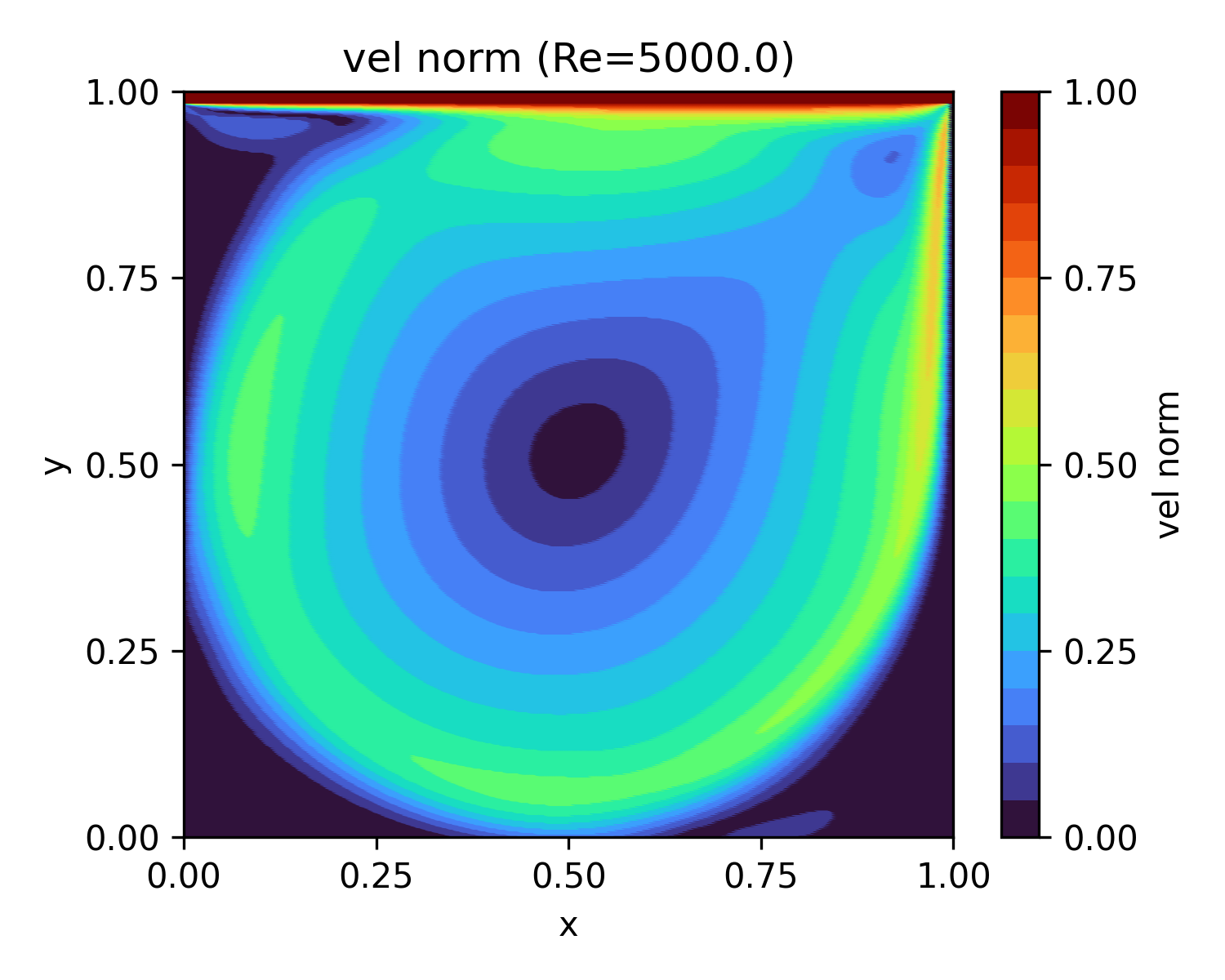 |
 |
 |
 |
Tested environment:
- numpy == 1.22.4
- matplotlib == 3.5.2
MIT License