pqc-attacks

Introduction

This repository contains Qiskit code to implement the quantum version of the heuristic GaussSieve algorithm proposed in [1] by Micciancio and Voulgaris to solve the Shortest vector problem (SVP) on lattices. First, we present the GaussSieve algorithm and a modification that uses hashing techniques. We then proceed with a brief high-level explanation of our code as well as the bottlenecks of our approach. Note that this code serves as a proof of concept and a starting point for a more thorough resource estimation of these types of quantum attacks. For a more detailed and technical overview of the code please refer to the documentation.

GaussSieve (with hashing)

We now present the pseudocode of GaussSieve (taken from [1]) along with a version that uses hashing (colored in blue). For more details on how hashing can be used to speed up GaussSieve and which hash families $\mathcal{H}$ provide speedups, refer to [2]. The constants $k$ and $t$ are dependent on the hash family $\mathcal{H}$ while a good value for the number of collisions $c$ can be experimentally determined (the original paper suggests $c=500$ is good enough).

Notice how GaussReduce is implementing two searches. In the quantum setting, by replacing them with Grover's algorithm we achieve a (theoretical) quadratic speedup over the classical version. This is what the code in this repository is implementing.

Encoding vectors

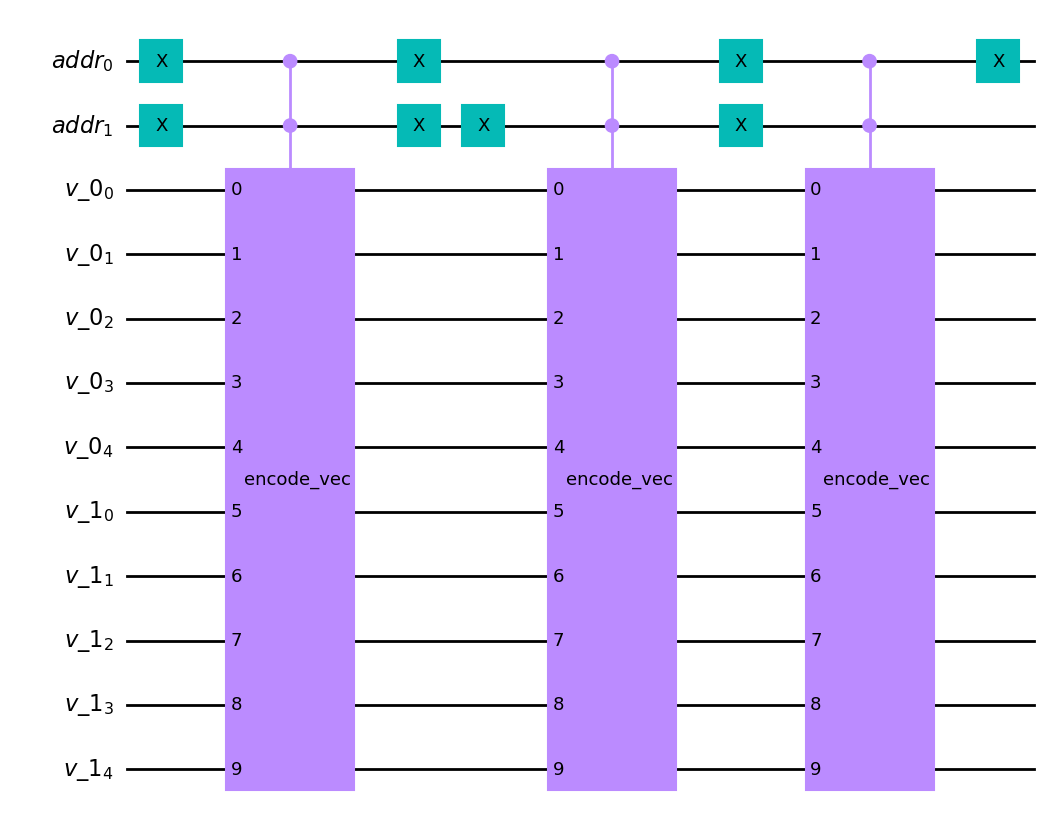
Since vectors can have negative elements, encoding them into a quantum computer is not as simple as just encoding their binary representations. To handle the signs we store an extra (qu)bit for each vector element representing its sign. This is known as the sign-magnitude representation of a signed integer. Therefore, the number of bits used for the storage of integers needs to be specified in advance. For example, the representation of $-2$ using $5$ bits in sign-magnitude format is $\textcolor{red}{1}0010$ whereas $2$ is represented as $\textcolor{red}{0}0010$. All arithmetic operation oracles such as norm calculation, addition, subtraction as well as comparison oracles are implemented with that representation in mind.

Note: No overflow test is performed. The user should select an appropriate number of bits beforehand, accounting for all operations.

Quantum RAM

To store the list $L$ in a quantum computer the use of quantum random access memory (qRAM) is required. We opted to implement a simple qRAM model with an address and a memory register that "loads" each element to its corresponding position. The qRAM circuit for a list containing three vectors of dimension 2, where each vector elements is encoded in $5$ bits, looks like this:

Grover search

The main part of this project is the implementation of oracles to perform the searches in the GaussReduce procedure. The code implementing those oracles is located in attacks/grover/oracles.py. These oracles are meant to be used with the built-in AmplificationProblem class in Qiskit. Following the notation of the linked tutorial, state_preparation consists of the qRAM circuit with Hadamard gates on the address register, a register encoding $\mathbf{p}$ as well as the necessary ancillas (to match the ancillas of the oracle). Finally, is_good_state is a function that (classically) checks if the returned list element has the required property. The pseudocode for is_good_state (for either one of the two searching problems) would look like this:

def is_good_state(measured_bitstring):
    isolate the solution vector L[i] from measured_bitstring
    isolate the vector p from measured_bitstring
    calculate the norms of L[i], p and p-L[i]
    if the norms satisfy the searching condition:
        return True
    return False

Bottlenecks

Due to the large number of qubits needed to perform all the operations the code cannot be executed in a simulator, even for small instances of the problem.
Due to the limited capabilities of quantum SDKs, implementing a fully capable qRAM is extremely difficult. The current architecture cannot handle list updates without having to rebuild the qRAM from scratch. This of course eliminates any quantum advantage since we already need $\mathcal{O}(|L|)$ time just to prepare the Grover circuit. We argue however that an actual (future) quantum computer will have these capabilities, much like a classical computer.
In the same spirit, we assume that stacks and hashtables will be easy to implement in a quantum computer without significant extra cost, even though we chose not to implement them here.

Testing the code

Since simulating the full code is beyond the capabilities of standard HPC clusters we opted to test each oracle separately. Because all of them are classical in nature (there is no entanglement), we can simulate them easily using Qiskit's matrix product state simulation method. The tests we wrote can be found in the tests/ directory and are run automatically every time new code is pushed to the repository, thus providing assurance on the correctness of the code.

References

[1] Daniele Micciancio and Panagiotis Voulgaris. Faster exponential time algorithms for the shortest vector problem. In Proceedings of the twenty-first annual ACM-SIAM symposium on Discrete Algorithms, pages 1468–1480. SIAM, 2010

[2] Thijs Laarhoven. Search problems in cryptography: from fingerprinting to lattice sieving. 2016.

Scinawa / pqc-attacks