BzMeshBandsDos

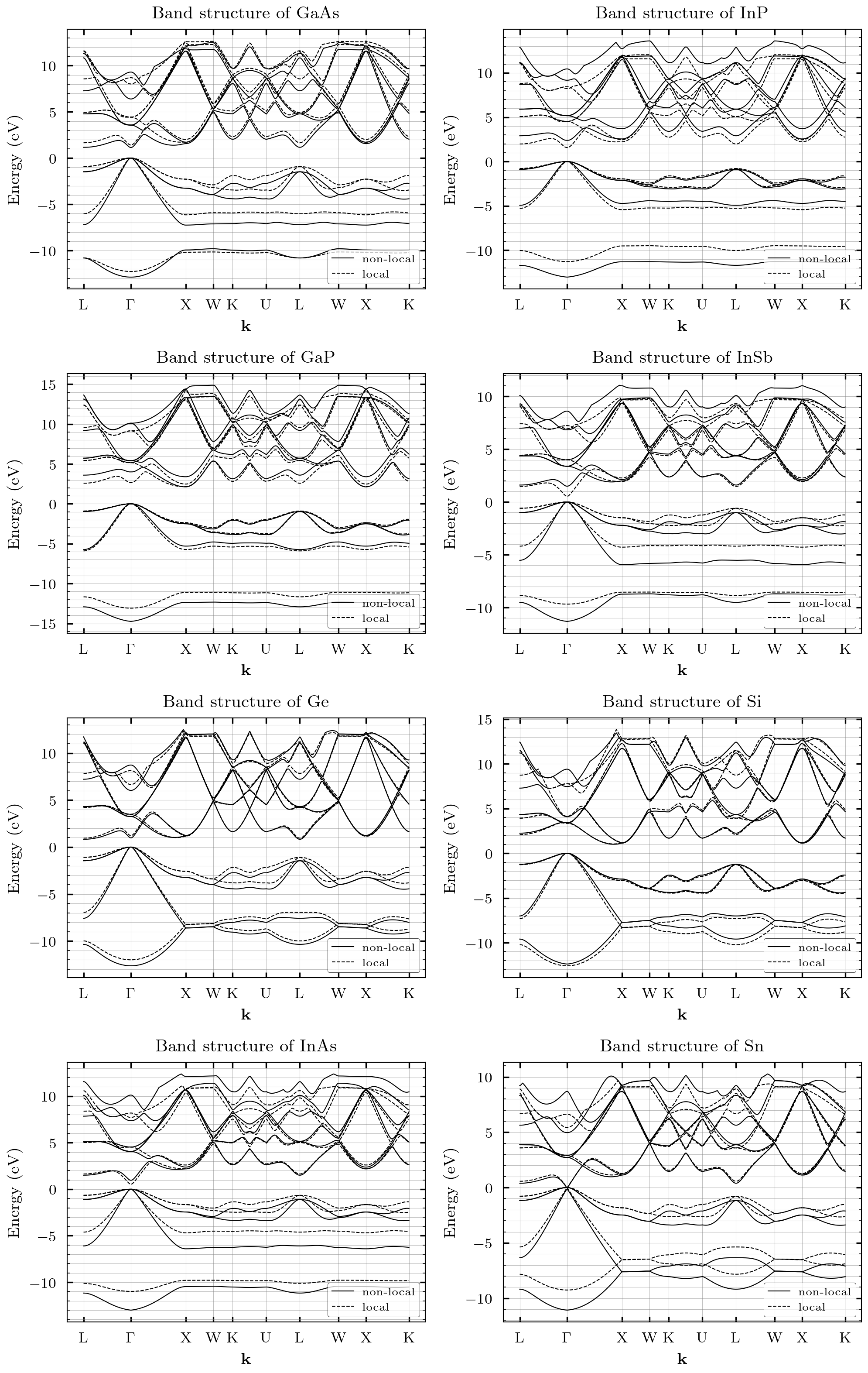
Band structure and DOS computation using empirical pseudopotentials on the full Brillouin-Zone. It includes the following features:

Standard EPM over high symmetry k-points in the Brillouin zone.
Calculation of the band structure and DOS on a mesh of k-points in the Brillouin zone.
Nonlocal corrections to the EPM.
Spin-orbit coupling (SOC) for the EPM band structure.
MPI and OpenMP parallelization.

This repository was initially a fork from : EmpiricalPseudopotential of Adrian Roman.

Features

You can do four types of calculations:

Band structure over a path of high-symmetry points in the Brillouin zone.
Band structure over all k-points of an input mesh of the Brillouin Zone (or a fraction of it).
Density of states over the all Brillouin Zone.
Dielectric function computation (q-dependent).

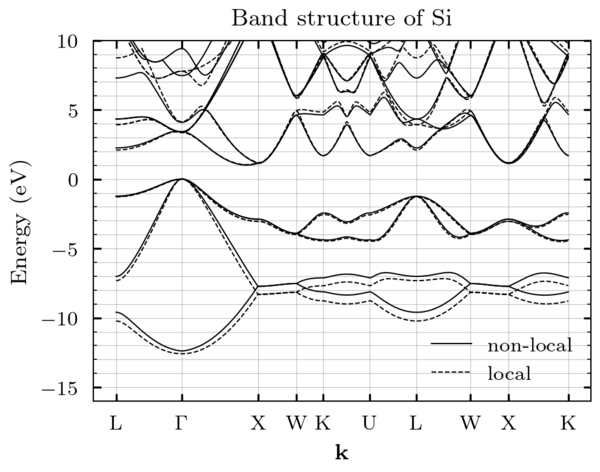
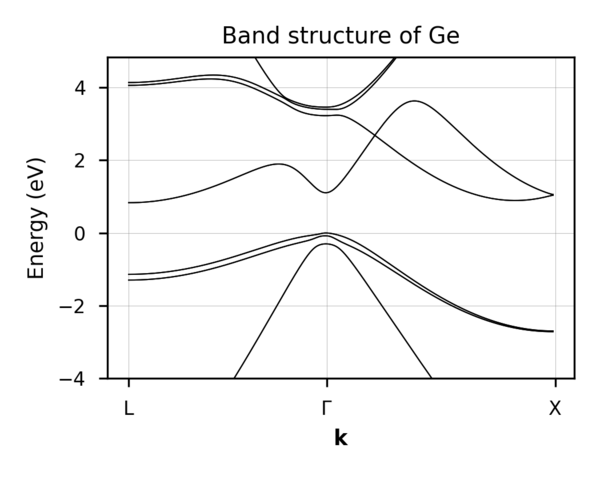
Compute the electronic band structure over a path of high-symmetry points (e.g. $L \Gamma XWKULWXK \Gamma$) for a given material, and plot the results.

The SOC can be included in the computation:

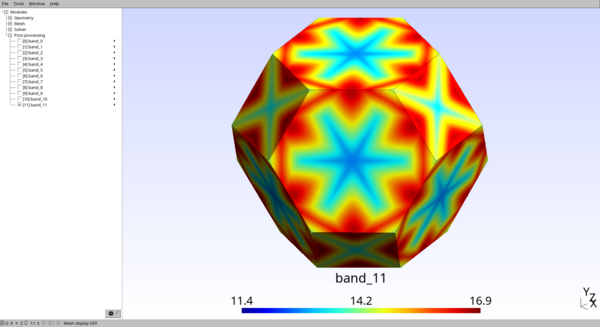
Compute the electronic band structure over all k-points of an input mesh of the Brillouin Zone (or a fraction of it). The result can then be visualized, for example, through iso-energy surface.

Compute the density of states over the all Brillouin Zone.

Dielectric function computation (q-dependent)

Build and Compilation

Dependencies

This project relies on these libraries:

You will also need standard packages such as CMake, Make, a C++ compiler, etc. A minimal installation command would look like:
sudo apt-get update && sudo apt-get install -y apt-utils cmake g++ libopenmpi-dev

If you don't have Eigen install on your system, the sources will be automatically fetched by CMake when you'll compile the project. You don't need to do anything. Eigen Website.

The tclap library is headers-only and embedded in the sources of the project. You do not need to install it.

You can install GMSH from sources straightforwardly :
Go wherever you want to install the library and run:
git clone https://gitlab.onelab.info/gmsh/gmsh.git && cd gmsh && mkdir build && cd build && cmake -DCMAKE_BUILD_TYPE=Release -DENABLE_BUILD_SHARED=1 -DENABLE_PRIVATE_API=1 .. && make -j 8 shared && make install/fast && cd .. && rm -rf gmsh
Find more informations on GMSH Website.

Compilation

git clone https://github.com/RemiHelleboid/EmpiricalPseudopotential.git
cd EmpiricalPseudopotential
mkdir build && cd build
cmake ..
make

Usage

Band structure plot over a path of high symmetry points

To plot the band structure over a path $LKW \Gamma XWL \Gamma K$ for a given materials, use:
./apps/EmpiricalPseudoPotentialMain -m Si -b 16 -N 2000 -n 10 -r output_dir -j 4 -p LGXWKULWXKG -C -P

The -m Si sets the material on which the band structure is computed to Silicon.
The -b 16 option means to compute and export 16 bands.
The -N 2000 option means that the path will be discretized in 2000 points.
The -n 10 option specifies the number of nearest neighbors used to compute the band structure.
The -C option means that the nonlocal corrections are used.
The -r output_dir means that the results of the computation will be stored in the output_dir directory (it is created if it does not exist yet).
The -j 4 option requires the computation to be run with parallelization on 4 CPUs.
The -p LGXWKULWXKG option specifies the path on which the band structure must be computed. G stands for $\Gamma$.
The -P option will trigger a call to a python script that will plot the calculated band structure after it has been computed.

Additional possibilities

If you don't specify the material with the -m SymBol option, the computation will be done for all the available materials.
If you want to get all material on many different paths, use the -A option, and don't specify either material or path.
Use ./apps/EmpiricalPseudoPotentialMain --help to display the help of the program.

Outputs

The energies at each point in the path, for each band, is stored in a file with the form EEP_Si_nb_bands_16_path_LGXWKULWXKG_size_basis_137.txt.
If the -P option was set, the plot of the band structured is also stored as .png and .pdf files.

Band structure computation over a mesh of the Brillouin Zone

To compute the electronic band structure over a mesh of the Brillouin zone, the command is:
./apps/BandsOnBZ -f bz_mesh.msh -m Si -b 12 -n 10 -C -j 8 -o output_file

The -m Si sets the material on which the band structure is computed to Silicon.
The -C option means that the nonlocal corrections are used.
The -b 12 option means to compute and export 16 bands.
The -j 8 option requires the computation to be run with parallelization on 8 CPUs. (OpenMP)
-o output_file can be used to set the name of the output file.

MPI
This program has an MPI version, for the same arguments as previously, the command is:
mpirun -np 8 ./apps/mpiBandsOnBZ -f bz_mesh.msh -m Si -b 12 -n 10 -o output_file

The parallelization is performed over the k-points of the BZ mesh.

Output

The result of the computation, i.e. the energy of each band at each vertex of the input mesh, is stored as follows: for each band the energies are store as a gmsh "view" which is the name for the physical data (scalar, vector field, tensor, ...) in the mesh.

Density of States Computation

The command to compute the Density of State is:
./apps/DOS_MeshBZ -f input_mesh_with_bands.msh -m Si -b 12 -e 500 -j 8 -P

The -f input_mesh_with_bands.msh the mesh file with the energy bands computed, resulting from the computation with BandsOnBZ program.
The -m Si sets the material on which the band structure is computed to Germanium.
The -b 12 the number of bands to consider, here: 16 bands.
The -e 500 option sets the number of energies with whom the energy range of each band is discretized.
The -j 8 option requires the computation to be run with parallelization on 8 CPUs.
The -P option will trigger a call to a python script that will plot the density of states after it has been computed.
-o output_file can be used to set the name of the output file.

MPI
This program has an MPI version, for the same arguments as previously, the command is:
mpirun -np 8 ./apps/mpiDOS_MeshBZ -f input_mesh_with_bands.msh -m Si -b 12 -e 500 -P

The parallelization is performed over the bands and the energies.

Performances

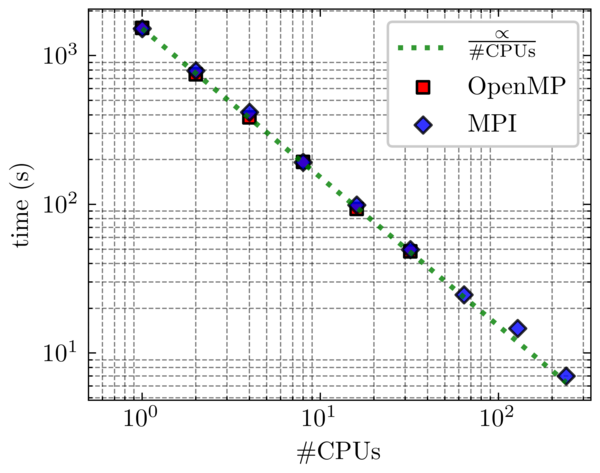
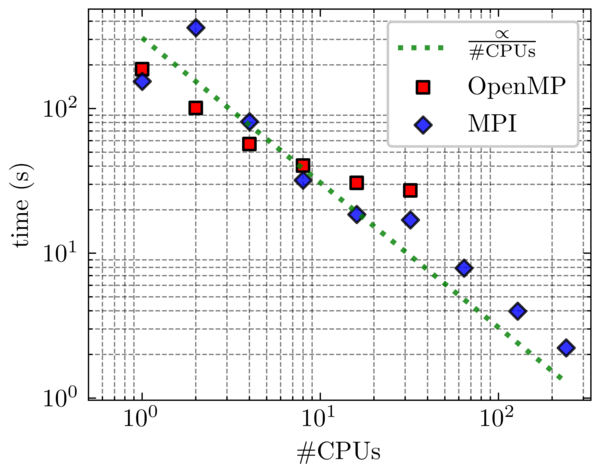
This section reports some performances of the code. We show comparison between parallelization with OpenMP and MPI. The numbers are shown only as a rough estimation, and one should not rely to much on the accuracy here.

Band structure computation

Band structure computation of Silicon for 16 bands, on a full BZ mesh of around 300K points with local EPM.

For band structure code, the parallelization is done over the k-points. Computation for every k-points is completely independent from the others, which leads to a very good scaling, as the above image shows. MPI enables to reach higher number of cores, so that the total computation time falls under one minute.

Density of states computation

Brillouin Zone Meshing

To get the required mesh of the Brillouin Zone, you can use the BZ.py script from the great J. Grebot, there: fcc-bz-mesh.

Available Materials

If you have data for materials that are not yet available in the code, feel free to contact us, we would be glad to add it.

Material	Local	Nonlocal
Si	Yes	Yes
Ge	Yes	Yes
GaP	Yes	Yes
GaAs	Yes	Yes
AlSb	Yes	No
InP	Yes	Yes
InAs	Yes	Yes
InSb	Yes	Yes
AlAs	Yes	No
ZnSe	No	Yes
CdTe	No	Yes

Comparison of the standard EPM with the nonlocal EPM for 8 materials.

References

Cohen, M. L. & Bergstresser, T. K. Band Structures and Pseudopotential Form Factors for Fourteen Semiconductors of the Diamond and Zinc-blende Structures. Phys. Rev. 141, 789–796 (1966).
Chelikowsky, J. R. & Cohen, M. L. Nonlocal pseudopotential calculations for the electronic structure of eleven diamond and zinc-blende semiconductors. Phys. Rev. B 14, 556–582 (1976).
Pötz, W. & Vogl, P. Theory of optical-phonon deformation potentials in tetrahedral semiconductors. Phys. Rev. B 24, 2025–2037 (1981).

Acknowledgements

Adrian Roman for the initial version of the code.
Jeremy Grebot for the BZ meshing script.
Marco Pala and Alessandro Pilotto: support for the non-local corrections.

RemiHelleboid / UltimateEPM