Kahsolt / Adiabatic-Linear-Solver-QPanda

Block Encodings & Quantum Discrete Adiabatic Linear-systems Solver implemented in QPanda (C++)

Adiabatic-Linear-Solver-QPanda

Block Encodings & Quantum Discrete Adiabatic Linear-systems Solver implemented in QPanda (C++)
第三届CCF“司南杯”量子计算编程挑战赛-通用赛道 决赛

---

比赛页面: 第三届CCF“司南杯”量子计算编程挑战赛通用赛道 队名: 我吃两个
得分: 85.67 (复赛) / 81.67 (答辩)
获奖: 三等奖 (wtf???

👉 初赛的 repo 在这里：CCF-3rd-Pilot-Cup-first-stage

Quickstart

• git clone https://github.com/Kahsolt/QLSDA-QPanda
  • add --recursive if you want QPanda as well
• install the C++ version QPanda, building from source... 😈
  • modify QPANDA_INSTALL_DIR in CMakeLists.txt according to your installation
• just run make or bash ./run.sh 😀🎉

This is the demo run for final linear solver solution:

ℹ Note that there are two folders containing source files:

• /playground: pennylane tutorials, pure numerical simulations for quick idea verification, debugging scipts
• /src: the real quantum logical circuit implementation in QPanda (C++) and PyQPanda (python)

Implementation

⚪ block encoding

👉 详细文档参见 BlockEncoding.md
😈 BlockEncoding 可能是一个非常危险的突破性技术：以后人们只是基于线性代数去设计算法，然后调用 block_encode + matrix_decompose 来在量子计算机上运行一切程序

Method	restriction	gate implementation	sub-normalizer	ancilla qubits	complex-value support
QSVT-like	$ σ_{max} = ||A||_2 \leq 1 $	use matrix_decompose methods (cannot generally implement with $ \mathcal{O}(poly(n)) $ gates)	-	1	✅
LCU	$ A = \sum\limits_{k=0}^{N-1} \alpha_k U_k $	$ U_A = \mathrm{PREP}^\dagger \cdot \mathrm{SEL} \cdot \mathrm{PREP} $	$ 1 / \sum_k |\alpha_k| $	$ \lceil log_2(k) \rceil $	❌
ARCSIN	$ d $-sparse $, |a_{ij}| \le 1 $	$ U_A = (I_1 \otimes H^{\otimes n} \otimes I_n) (I_1 \otimes \mathrm{SWAP}) O_A (X \otimes H^{\otimes n} \otimes I_n) $	$ 1 / 2^n $	$ n + 1 $	✅
FABLE	$ d $-sparse $, |a_{ij}| \le 1 $	$ U_A = (I_1 \otimes H^{\otimes n} \otimes I_n) (I_1 \otimes \mathrm{SWAP}) O_A (I_1 \otimes H^{\otimes n} \otimes I_n) $	$ 1 / 2^n $	$ n + 1 $	❌

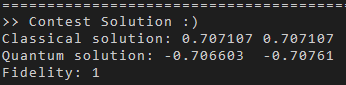
Precision Check	Generated Circuit

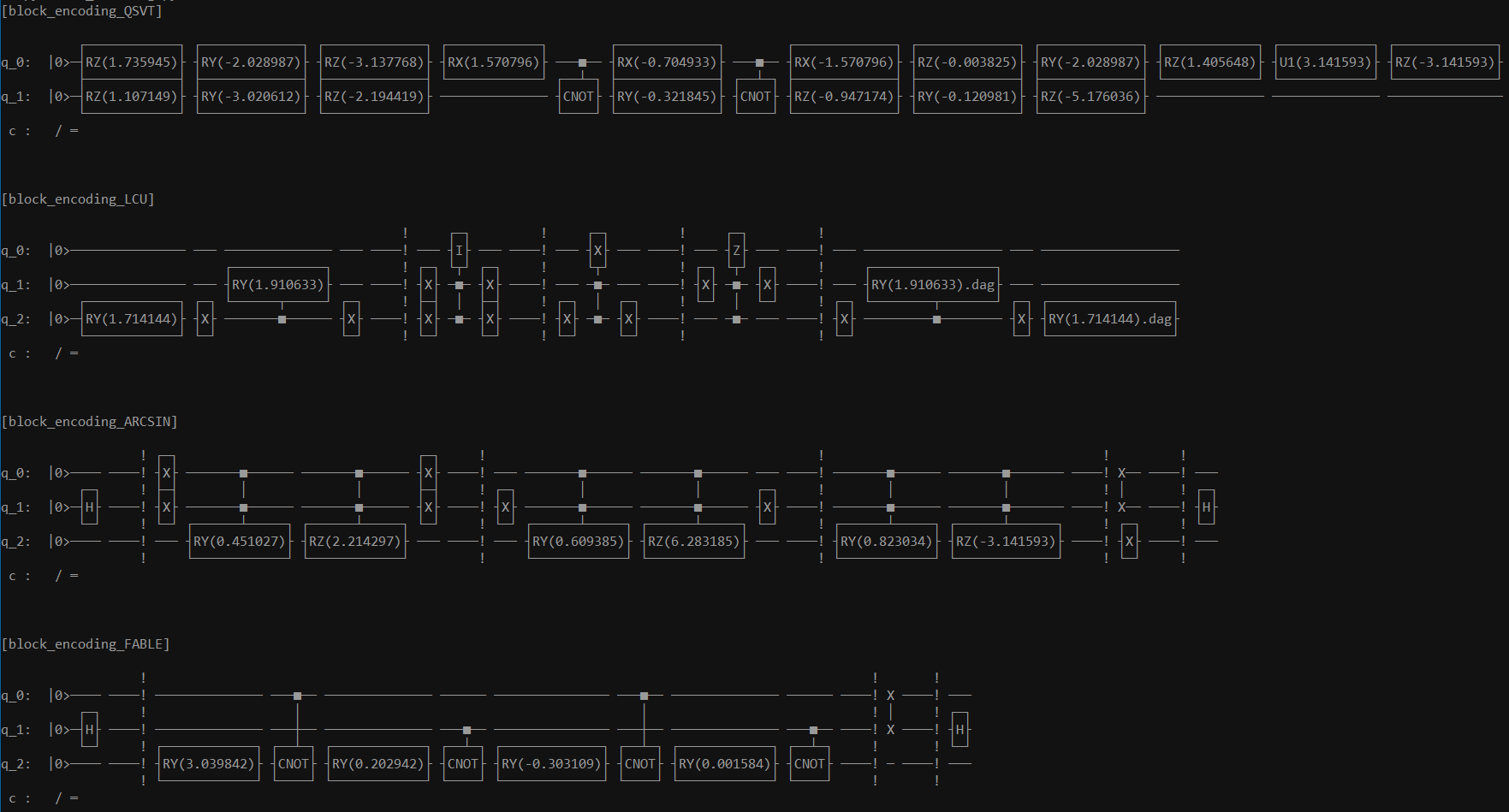⚪ adiabatic-inspired linear system solver

👉 详细文档参见 LinearSolver.md

Method	year	sched func $ f(s) $	time complexity	query complexity (EF paper listed)	query complexity (QDA paper listed)
RM (algo-1)	2018	$ \text{v-func} $	$ \mathcal{O}(\kappa^2 \mathrm{log}(\kappa) / \epsilon) $	$ \mathcal{O}(\kappa / \epsilon) $
RM (algo-2)	2018	$ \text{v-func} $	$ \mathcal{O}(\kappa \mathrm{log}(\kappa) / \epsilon) $	$ \mathcal{O}(\kappa / \epsilon) $	$ \mathcal{O}(\kappa \mathrm{log}(\kappa) / \epsilon) $
vanilla AQC	2019	$ \text{linear} $	$ \mathcal{O}(\kappa^3 / \epsilon) $	$ \mathcal{O}(\kappa^2 / \epsilon) $
AQC(P)	2019	$ \text{poly} $	$ \mathcal{O}(\kappa / \epsilon) \sim \mathcal{O}(\kappa \mathrm{log}(\kappa) / \epsilon) $	$ \mathcal{O}(\kappa \mathrm{log}(\kappa) \mathrm{loglog}(\kappa)) $ for $ \mathcal{O}(1) $ precision
AQC(EXP)	2019	$ \text{exp} $	$ \mathcal{O}(\kappa \mathrm{log}^2(\kappa) \mathrm{log}^4(\mathrm{log}(\kappa)/\epsilon)) $	$ \mathcal{O}(\kappa \mathrm{polylog}(1 / \epsilon)) $	$ \mathcal{O}(\kappa \mathrm{polylog}(\kappa / \epsilon)) $
EF (partial)	2019	$ \text{poly} $		$ \mathcal{O}(\kappa \mathrm{log}(1 / \epsilon)) $	$ \mathcal{O}(\kappa \mathrm{log}(\kappa / \epsilon)) $
QDA (partial)	2021	$ \text{poly} $			$ \mathcal{O}(\kappa \mathrm{log}(1 / \epsilon)) $
EQLS (partial)	2023	$ \text{v-func} $	$ \mathcal{O}(\kappa \mathrm{log}(\kappa / \epsilon)) $

ℹ Note that $ \mathcal{\Omega}(\kappa \mathrm{log}(1 / \epsilon)) $ is the theoretical lower bound for sparse QLSP

Obviously there is an argument between QDA and EF, that EF overlooked a factor by $ \mathrm{log}(k) $? 🤔

• EF := AQC(P) + EF = $ \mathcal{O}(\kappa \mathrm{log}(\kappa) \mathrm{loglog}(\kappa)) + \mathcal{O}(\kappa \mathrm{log}(1 / \epsilon)) $
• QDA := QWalk + EF = $ \mathcal{O}(\kappa) + \mathcal{O}(\kappa \mathrm{log}(1 / \epsilon)) $
• EQLS: = RM + EF OK then, QDA might be right: EF forgot to count for its AQC(p) part

references

• dev
  • QPanda (C++): https://github.com/OriginQ/QPanda-2
  • Eigen lib: https://eigen.tuxfamily.org/dox/index.html
  • pennylane: https://github.com/PennyLaneAI/pennylane
• thesis
  • [1] Optimal scaling quantum linear systems solver via discrete adiabatic theorem: https://arxiv.org/abs/2111.08152
    • report lecture (2022): https://www.youtube.com/watch?v=qEA37SfxPEs
  • [3] Quantum algorithm for systems of linear equations with exponentially improved dependence on precision: https://arxiv.org/abs/1511.02306
    • report lecture (2015): https://www.youtube.com/watch?v=IdCCn2X5dW4
  • [4] Hamiltonian Simulation by Qubitization: https://arxiv.org/abs/1610.06546
  • [5] Quantum linear system solver based on time-optimal adiabatic quantum computing and quantum approximate optimization algorithm: https://arxiv.org/abs/1909.05500
    • report lecture (2020): https://www.youtube.com/watch?v=RiRaHGEvlZE
  • The discrete adiabatic quantum linear system solver has lower constant factors than the randomised adiabatic solver: https://arxiv.org/abs/2312.07690
    • report lecture (2024): https://www.youtube.com/watch?v=WfByvOf3N3Y
  • Quantum Computation by Adiabatic Evolution: https://arxiv.org/abs/quant-ph/0001106
  • Quantum state preparation by phase randomization: https://arxiv.org/abs/0903.1652
  • Quantum algorithms for systems of linear equations inspired by adiabatic quantum computing: https://arxiv.org/abs/1805.10549
  • Optimal polynomial based quantum eigenstate filtering with application to solving quantum linear systems: https://arxiv.org/abs/1910.14596
  • Efficient quantum linear solver algorithm with detailed running costs: https://arxiv.org/abs/2305.11352
• Block Encoding
  • pennylane tutorials
    • Intro to QSVT: https://pennylane.ai/qml/demos/tutorial_intro_qsvt/
    • QSVT in Practice: https://pennylane.ai/qml/demos/tutorial_apply_qsvt/
    • Linear combination of unitaries and block encodings: https://pennylane.ai/qml/demos/tutorial_lcu_blockencoding/
    • Block encoding with matrix access oracles: https://pennylane.ai/qml/demos/tutorial_block_encoding/
  • Lecture - The block-encoding: https://www.ias.edu/sites/default/files/Tang%20qsvt_lect_1.pdf
  • Hamiltonian simulation with nearly optimal dependence on all parameters: https://arxiv.org/abs/1501.01715
  • Explicit Quantum Circuits for Block Encodings of Certain Sparse Matrices: https://arxiv.org/abs/2203.10236
  • FABLE: Fast Approximate Quantum Circuits for Block-Encodings: https://arxiv.org/abs/2205.00081

---

by Armit 2024/05/13