3x3-2D-transformations_demo

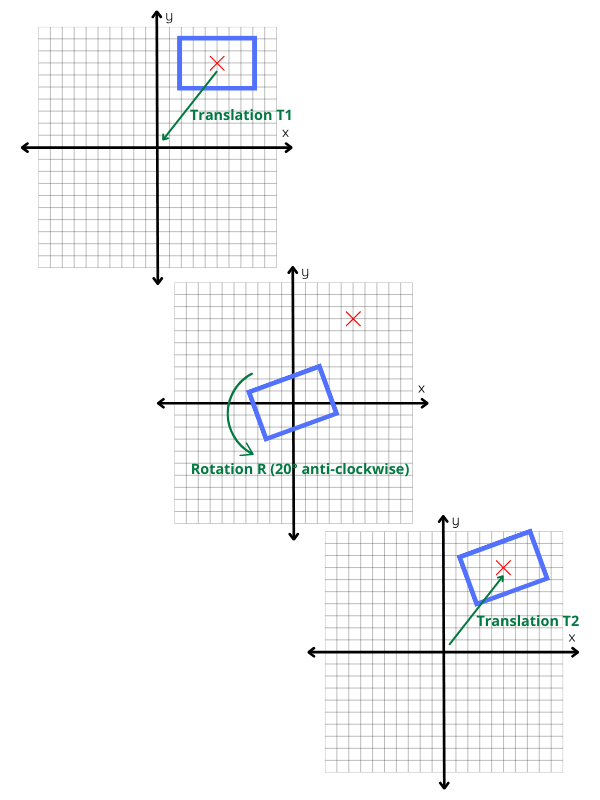
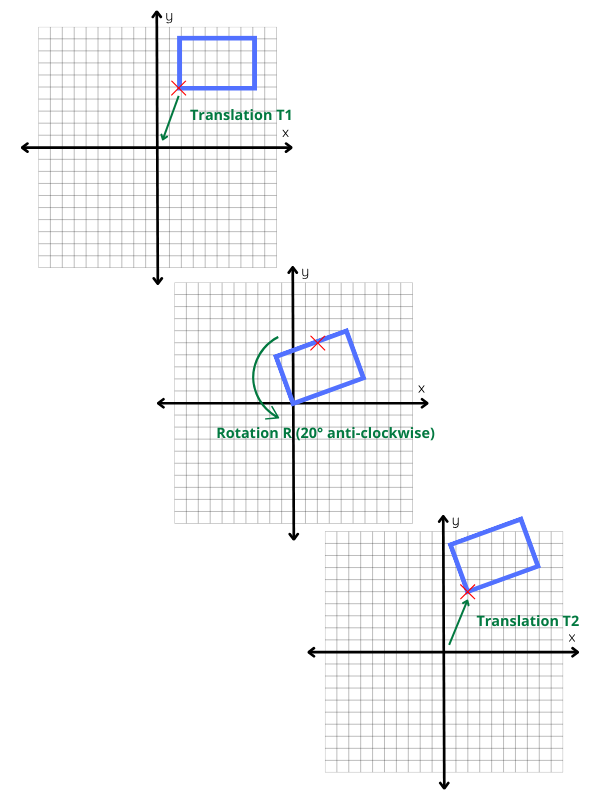
Shows 3x3 matrices use for simple 2D transformations (translation, rotation, scaling…)

The translation problem

As seen here we can use 2x2 matrices to performs some 2D transformations (rotations, flips…) but this method has major drawbacks : we can’t perform translation, some transformations lead to unwanted translations, and the transformations are relative to the coordinates origin/axes.

How could we uses matrices to perform translations ?

Point translation of 10 units along the x axis and 8 units along the y axis, we can just be expressed by :

$$ x_t = x + 10 $$

$$ y_t = y + 8 $$

but 2x2 matrices can’t express such transformation by multiplication (I will represent coordinates by a row vector, when using a column vector just transpose the matrices used) :

$$ \begin{bmatrix} x & y \end{bmatrix} . \begin{bmatrix} a & b \\\ b & c\end{bmatrix} = \begin{bmatrix} x.a + y.b & x.c + y.d\end{bmatrix} $$

Each term is either a multiple of x or a multiple of y. We can’t add a constant.

Note : Of course, this operation is trivial if we add two 2x1 matrices, but the point here is to limit to product operation only, because we then could chain transformations by chaining multiplications.

However, if we note that

$$ x + 10 = x.1 + y.0 + 1.10 $$

we can write :

$$ \begin{bmatrix}x & y & 1\end{bmatrix} . \begin{bmatrix} 1 \\ 0 \\ 10 \end{bmatrix} = \begin{bmatrix} x + 10 \end{bmatrix} $$

for y :

$$ \begin{bmatrix}x & y & 1\end{bmatrix} . \begin{bmatrix} 0 \\ 1 \\ 8 \end{bmatrix} = \begin{bmatrix} y + 8 \end{bmatrix} $$

and finally :

$$ \begin{bmatrix}x & y & 1\end{bmatrix} . \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 \end{bmatrix} $$

So, if we accept to add a third term equal to 1 at the coordinates (that will be ignored when drawing figures) we can perform translation with a 3x3 matrix multiplication :

$$ \begin{bmatrix} x & y & 1 \end{bmatrix} . \begin{bmatrix} 1 & 0 & 0 \\\ 0 & 1 & 0 \\\ t_x & t_y & 1 \end{bmatrix} = \begin{bmatrix} x + t_x & y + t_y & 1\end{bmatrix} $$

2D coordinates with such a third term are called homogenous coordinates, with a condition on the third term :

$$ \begin{bmatrix} h.x & h.y & h \end{bmatrix} $$

h=1 is often a convenient choice in 2D (other values can be better choices in 3D)

3x3 matrices for other transformations

Following the same process, we can build 3x3 matrices for the transformations seen before :

Rotation (clockwise)

$$ \begin{bmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

Rotation (anti-clockwise)

$$ \begin{bmatrix} \cos \theta & \sin \theta & 0 \\ -\sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

Note : to obtain an anti-clockwise rotation, we could also just use -θ with the clockwise rotation matrix

Horizontal flip

$$ \begin{bmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

Vertical flip

$$ \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

Scaling

$$ \begin{bmatrix} S_x & 0 & 0 \\ 0 & S_y & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

x-axis shearing/tearing

$$ \begin{bmatrix} 1 & 0 & 0 \\ S_x & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

y-axis shearing/tearing

$$ \begin{bmatrix} 1 & S_y & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$

All those 3x3 matrices correspond to axes/origin centered transformations, as with 2x2 matrices. Let’s see how the new possibility of translation can help us to generalise those transformations, via a combination of transformations.

Generalized transformations

To process a rotation centered on any point, we just have to follow a 3 steps process : translate the figure to bring the rotation point to the origin, rotate, and translate back the figure to its original position

this 3 steps process is correct for any chosen point, here the bottom left vertex of the rectangle :

How do we combine those 3 transformations ? By successively applying the corresponding transformation matrices (translation consist to bring the point C - center of the rotation - of coordinates $$\begin{bmatrix} C_x & C_y \end{bmatrix} $$ to the origin $$ \begin{bmatrix} 0 & 0 \end{bmatrix} $$

Perform the rotation and then translate back the figure to C. It means that C_x and C_y are not only the coordinates of C, but also the parameters of the translation.

$$ \begin{bmatrix} x & y & 1 \end{bmatrix} . T1 . R . T2 = \\ \begin{bmatrix} x & y & 1 \end{bmatrix} . \begin{bmatrix} 1 & 0 & 0 \\\ 0 & 1 & 0 \\\ -C_x & -C_y & 1 \end{bmatrix} . \begin{bmatrix} \cos 20\degree & \sin 20\degree & 0 \\ –\sin 20\degree & \cos 20\degree & 0 \\ 0 & 0 & 1 \end{bmatrix} . \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ C_x & C_y & 1 \end{bmatrix} $$

We can of course multiply the transformations matrices together to obtain a combined transformation matrix, using the associative property of matrix product. Just be aware that matrix product however is non-commutative : the order is important.

$$ T1 . R . T2 = \\ \begin{bmatrix} \cos 20\degree & \sin 20\degree & 0 \\ -\sin 20\degree & \cos 20\degree & 0 \\ C_x(1-\cos 20\degree) + C_y \sin 20\degree & C_y(1-\cos 20\degree) - C_x \sin 20\degree & 1 \end{bmatrix} $$

We can apply the same logics to all transformations.

See the source code comments for more details !

How to

To run the demo :

make run

Build .js executable for the web :

make js

To do

Give user the ability to move (translate) only the figure
Explicit the chaining of transformation/multiplication. Why not record all transformations in a string given by the user, for exemple 'rmtsr' -> rotate / translate (move) / shear (tear) / scale / rotate) and show the resulting transformation matrix obtained by multiplications of primitives/transformation matrix ?

Issues

The .js version seems to have some issues detecting simultaneous key press.
For simplicity, a lot of transformations parameters are hard coded, not very elegant.

Jehadel / 3x3-2D-transformations_demo