COMPSCI4004 Artificial Intelligence H - Coursework
We will explore an approach to select an optimal set of training instances for supervised learning. Specifically, we are going to work with the MNIST 1 dataset, a popular dataset for hand-written digit recognition. Some examples of the images in the MNIST dataset are illustrated in Figure 1.
Figure 1: Examples of the images in the MNIST dataset.
Classifying the images in MNIST is no longer a big challenge since a lot of advanced deep learning models have been proposed over the years and the top performers can achieve a classification accuracy of over 99% (see Image Classification on MNIST).
Having said that, most of the existing methods are based on the assumption that the annotation of the data is reliable and train the model accordingly. However, it is possible that the dataset contains inaccurate annotation due to human mistakes or even contaminated data. As a result, the performance of the trained model will be degraded.
We implemented a simulated workflow of learning with corrupted labels 1, which will act as a starting point for implementing your own solutions.
The notebook provides functions to corrupt labels with common types of mistakes (specific to this hand-written digit classification task), such as labelling a “3” as a “8” (and vice versa), a “1” as a “4” or “7” etc. A parameter that controls how many annotations will be corrupted in the dataset (i.e., how noisy is the data) by specifying a value for noise probability (
Some utility functions to start the supervised (parametric) training with the (noisy) labelled examples using trainAndEvaluateModel() are provided.
Points to note:
- We are not going to change the model architecture. This is considered frozen.
- We are going to investigate if changing the dataset (seeking to leave out the noise from the training set) improves the accuracy over the test set.
You don’t need to understand how the classification model really works (it’s a one-layer 2D convolution network, which is covered in the Deep Learning and Computer Vision courses). The model’s reference implementation is to be used only to evaluate the quality of your training data (the better the trained model performs on the test set, the better is the quality of the training set).
This report discusses using a Genetic Algorithm (GA) to improve the model performance on the MNIST dataset using a supervised approach. The problem at hand involves dealing with potentially corrupted data within the dataset, impacting the performance of trained models. The methodology embraces a unique approach, tailoring the initial population of the GA by considering the class frequency differences within the corrupted MNIST dataset. This strategic bias towards underrepresented classes aims to enhance classification accuracy. The report outlines the steps involved in the algorithm, from initialising the population to transitioning to subsequent generations, incorporating key processes such as selection, crossover, and mutation. The focus is ensuring a diverse and efficient search through the solution space, balancing computational resources with the potential for reaching optimal or near-optimal solutions.
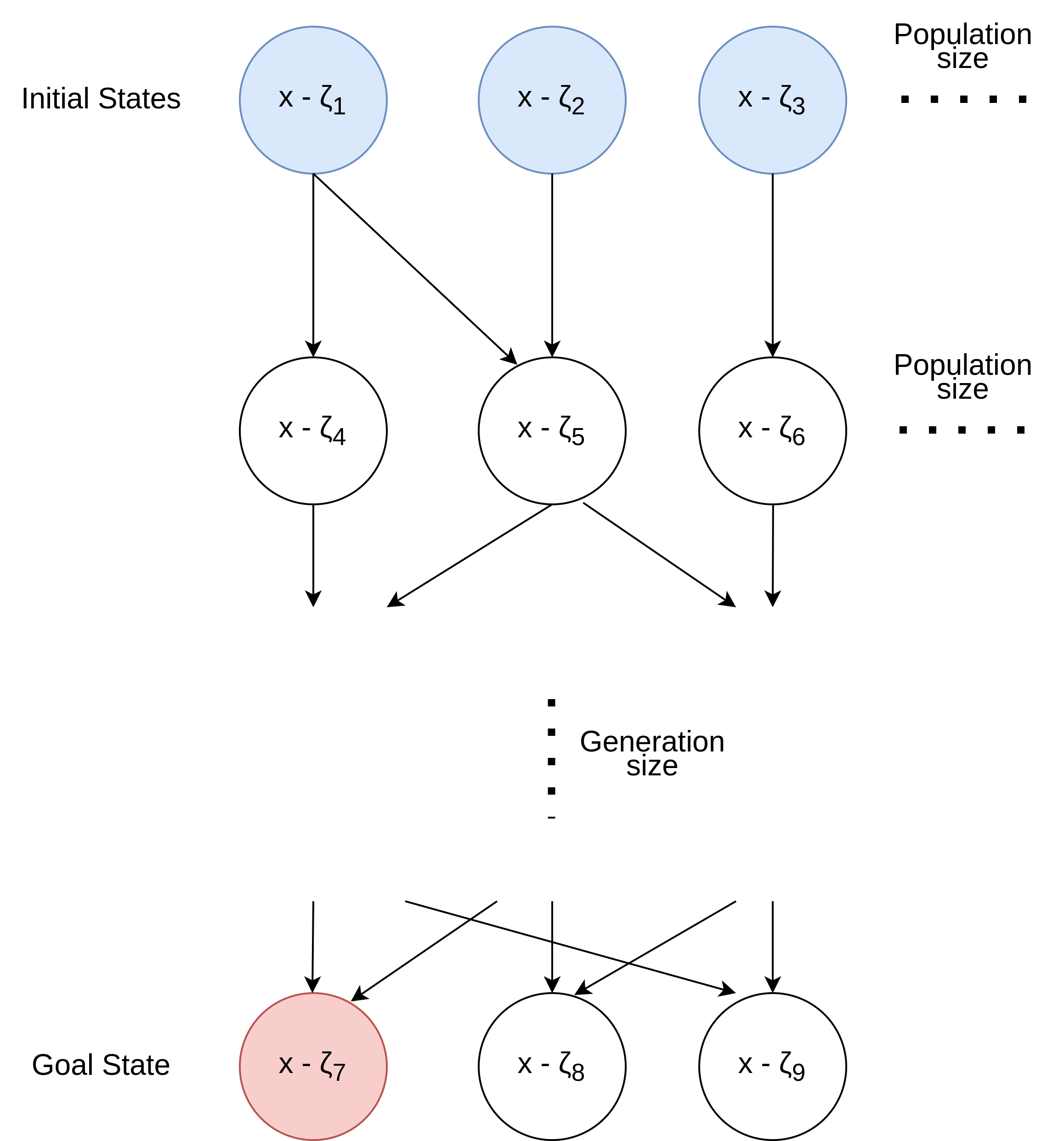
I chose to use the Genetic Algorithm to find the best possible state (goal state). As shown in Figure 1, we start with multiple initial states (in terms of the GA algorithm, they are called individuals in the population). The initial states are started almost randomly but not quite. Further details about this are discussed later in Section 3. These initial states create the first population in the generation.
The following actions create the subsequent generations: Selections, Crossover and Mutation.
Figure 1 shows the transition between the states.
This is done by selecting
My solution exploits the fact that the MNIST data set has roughly an equal number of data points for each digit class. Therefore, after corruption, the difference in frequency of the digits will only get bigger. This is shown in Table 1
| Digit | Before | After | Difference |
|---|---|---|---|
| 0 | 5923 | 6003 | 80 |
| 1 | 6742 | 6561 | -181 |
| 2 | 5958 | 5906 | -52 |
| 3 | 6131 | 6073 | -58 |
| 4 | 5842 | 6339 | 497 |
| 5 | 5421 | 5782 | 361 |
| 6 | 5918 | 5624 | -294 |
| 7 | 6265 | 5949 | -316 |
| 8 | 5851 | 5900 | 49 |
| 9 | 5949 | 5863 | -86 |
Table: Digit frequency in the MNIST data set
In the following sections, I will explain my implementation of the Genetic Algorithm.
Population in the Genetic Algorithm is a collection of individuals in a
generation. Individuals are the states representing (
By using the knowledge from Table 1, we can estimate the noise difference and, then, bias toward the underrepresented classes for better classifications. This calculations are done when creating the initial population (states) and is demonstrated in the following section of the code:
def create_population(population_size, input_size, y_train, bias_strength=100):
...
classes, freq = np.unique(y_train, return_counts=True)
class_frequencies =
max_freq = max(class_frequencies.values())
prioritisation_scores =
for _ in range(POPULATION_SIZE):
individual = np.ones(INPUT_SIZE, dtype=int)
...
if random.random() < ((prioritization_scores[class_label] / max_freq)*bias_strength):
individual[i] = 0
...
population = [tuple(individual) for individual in population]
return population
The "Prioritisation scores" is a dictionary of the weights of every digit in the data set. It looks like this:
Where the keys are the digit classes and the values are their weights (frequency relative to other classes).
Then we normalised it by dividing this value by the
When creating the population, we also don't allow duplicates (identical individuals). This will enable us to prevent processing identical individuals twice and improve the diversity in our initial states. In addition, we start with individuals, primarily 1s (i.e., prune most indexes). This makes the initial computations faster and allows us to perform more generations.
Afterwards, we evaluate the "fitness" of each individual by calling
the
I used caching to ensure fast training time with the
from functools import lru_cache
@lru_cache(maxsize=None)
def evaluate_fitness(model, individual):
...
return accuracy
After this, for every generation, the
In the selection step, we select $selection_size$ number of individuals
to stay to the next generation. The $selection_size$ is less than the
This is demonstrated in the following section of the code:
def select_individuals(population, fitness_scores, selection_size, battle_participants, elite_num):
...
while len(selected_individuals) < selection_size:
participants = random.sample(list(zip(population, fitness_scores)), battle_participants)
sorted_participants = sorted(participants, key=lambda x:x[1], reverse=True)
# append individual only, not fitness score:
selected_individuals.append(sorted_participants[0][0])
return selected_individuals
Elitism is performed before tournament selection to ensure that
This is shown in the following code:
def find_top_N_elements(population, fitness_scores, N):
...
for _ in range(N):
max_index = np.argmax(fitness_scores)
top_N.append(population[max_index])
fitness_scores[max_index] = -1
return top_N
def select_individuals(population, fitness_scores, selection_size, battle_participants, elite_num):
...
selected_individuals.extend(find_top_N_elements(population, fitness_scores, elite_num))
...
return selected_individuals
After selecting $selection_size$ individuals to carry over to the next
generation, we need to re-create the population to keep it at the
To do the crossover, we select two random individuals from the selected
individuals list and swap over
def crossover(individual_1, individual_2, crossover_rate, crossover_points):
if random.random() < crossover_rate:
crossover_points = random.sample(range(1, len(individual_1)), crossover_points)
crossover_points.sort()
new_individual_1 = individual_1[:crossover_points[0]] + individual_2[crossover_points[0]:crossover_points[1]] + individual_1[crossover_points[1]:]
new_individual_2 = individual_2[:crossover_points[0]] + individual_1[crossover_points[0]:crossover_points[1]] + individual_2[crossover_points[1]:]
return new_individual_1, new_individual_2
else:
return individual_1, individual_2
The mutation step is done on every new individual after the crossover
step. In the mutation step, we iterate over all the bits (called genes
in terms of GA) and flip that bit (mutate)
def mutate(individual, mutation_rate):
new_individual = []
for gene in individual:
if random.random() < mutation_rate:
new_individual.append(1 - gene) # flip the gene
else:
new_individual.append(gene)
return new_individual
After mutation, the accuracy (fitness) is re-evaluated on the new generation, and then we transition to the next generation by repeating the "selection" step. When the new population returned is exactly the same as the old population, this means that the algorithm has found the maximum value. This value is likely not optimal (global maximum) but rather a local maximum. Further analysis about the performance is done in Section 5.
The maximum accuracy after every generation is written to a "GA_0.csv" file to enable us to compare different hyperparameters and their effect on the algorithm performance.
The Genetic Algorithm is non-deterministic. This means that the results vary a bit at every run because of its random nature in the selection, crossover and mutation steps. That said, my solution achieved an accuracy of over 60% on some runsand more than 55% most of the time, which is above the baseline solution where indexes are pruned randomly, achieving an accuracy of about 49%.
The hyperparameters I used are listed in Table 2 alongside the values I chose for each.
| Parameter | Value | Description |
|---|---|---|
| Bias Strength | 100 | Bias strength |
| Population Size | 200 | Number of individuals in population |
| Selection Size | 160 | Number of individuals to select for next generation |
| Mutation Rate | 0.1 | Probability of mutating each individual |
| Crossover Rate | 0.5 | Probability of crossing over two individuals |
| Crossover Points | 3 | Number of crossover points |
| Generations | 100 | Number of generations |
| Battle Participants | 4 | Number of individuals to participate in a tournament |
| Elite Number | 1 | Number of elite individuals to keep from one generation to the next |
Table: Digit frequency in the MNIST data set
I will explain why I chose each of these values.
Bias strength is a multiplier to define how biased we should be toward the underrepresented classes in the dataset. It mainly affects the initial population because it is used only when creating the first generation (initial states). I tested a range of values from 1 to 1000, and my results are shown in Figure 2.
As shown in the plot, with a bias strength of 100, it is possible to get individuals in the initial population with accuracy level just below 60%. This means that the initial population already performs well. This helps us determine the maximum accuracy faster after generations as we don't start with random individuals but rather with individuals that already perform better than random.
As I mentioned, a bigger population means a higher diversity of solutions in the generation. However, this comes at a computational time cost. In Figure 6, I compared having the initial population sizes at 200, 100 and 10 and found that, more than 200 individuals, the computational time to calculate their accuracy (fitness) was getting much longer with a little accuracy improvement.
Therefore, around 200 was the best choice for the
A selection size is chosen to keep the best-performing individuals at every generation. I tried selection sizes of 30%, 50% and 90% of population size. Figure 10 shows the difference between them.
As shown in the plots, a larger selection size led to better results because most of the best candidates are maintained for later generations, increasing the population's overall performance. It is worth mentioning that a larger selection size means less computational time due to the decreased number of points that need to crossover or mutate. In addition, all choices of selection sizes lead to convergence at around generation 10, but the real difference appears in the computational time required to perform each of them. With 90% selection size, it took only 5 mins, while it took about 13 mins for 30% selection size and 10 mins for 50% selection size. The accuracy is also slightly better with higher selection size values as we can see about 1 to 2% improvement.
Crossover rate, crossover points and battle participants were selected
by trial and error. Crossover points decide how many sections from one
individual we should swap with another (e.g. 1 means one section, which
means half of the individual). This ensures that a variety of solutions
can be achieved, aiming to escape the local maximum. However, like
everything else, more points require more computational time. I chose
the values in Table 3, which gave me the best
The crossover step happens
The
| Parameter | Value |
|---|---|
| Crossover Rate | 0.5 |
| Crossover Points | 3 |
| Battle Participants | 4 |
Table: Crossover values
Mutation helps us escape a local maximum by discovering random variation of an individual (by mutating one or more of their genes), which might lead to the global maximum. This was also decided by trial and error, and I found that a relatively high value of 0.1 or 10% leads to better results compared to low values such as 0.01 or 0.05 (1 or 5%). So I chose to use 0.1.
In my solution, the population always converged before the 20th generation. I chose 100 generations as the top limit but never reached that limit. Further analysis of why this is the case is in Section 6.
Elitism guarantees that the best of the best individuals are kept for future generations and are not affected by the random nature of the tournament selection, crossover, or mutation. As shown in Figure 14, I tried with values 0, 1 and 2. However, an elite value bigger than 2 doesn't make sense, as it will make the population converge much quicker.
One of the problems my solution suffers from is an early convergence. My solution usually converges just before generation 10 due to a local maximum discovery. This prevents my solution from finding a better accuracy value and, therefore, better classification performance. We must implement more sophisticated crossover and mutation techniques to avoid this. A possible solution for the crossover is by implementing a dynamic crossover. Therefore, the crossover points and rate change dynamically as generations progress. By that, I mean that we might benefit from increasing the strength of crossover in the early generations but then reduce it as generations pass.
Regarding the mutation, we can track which genes generally make the accuracy better and force mutating them after a few generations to improve the overall performance of a population.
Another possible way to solve the early convergence problem is by using a hybrid approach. So, instead of solely depending on the Genetic Algorithm, we can use another approach alongside it. E.g. using Hill Climbing with Genetic Algorithm to search local branches and find the optimal solution for each. This might yield better results.
In this report, we presented a comprehensive exploration of using a Genetic Algorithm to enhance the selection process of training instances of the MNIST dataset in the presence of noisy data. The findings demonstrate the approach's effectiveness, significantly improving classification accuracy over a baseline model using random selection. While the solution often converges to a local maximum, suggesting limitations in exploring the entire solution space, the overall performance indicates promising results can be achieved using the GA algorithm. The potential improvements include dynamic crossover techniques and focused mutation strategies.