Simple implementation of U(1) gauge theory on lattice in 1 + 1 dimensions
We want to study pure gauge theory with group U(1), the action is:
$$
S_{E} = \frac{1}{4}\int d^2x F^{\mu \nu} F_{\mu \nu} = \frac{1}{2}\int d^2xF^2_{12}
$$
Instead of using the values on a grid, we must consider the link between two sites, this allows us to maintain gauge invariance; numerically we use two matrix, one for vertical link and one for horizzontal link.
In the case of U(1) the parallel transports are simply complex numbers:
$$
U_{\mu}(n) = e^{i \varphi(n)} \qquad \text{and} \qquad -\pi \leq \varphi(n) \leq \pi
$$
Where $\mu$ indicate the direction, temporal o spatial, and $n$ is the position.
In oue case the more general pure gauge and gauge invariant term is a closed loop of parallel transports which in our case is the so-called plaquette (in non abelian case we must condider the trace of loop):
$$
\Pi_{\mu \nu}=U_{\mu}(n)U_{\nu}(n+\mu)U_{\mu}^{-1}(n+\nu)U_{\nu}^{-1}(n)
$$
Using $U_{\mu}(n) \simeq e^{igaA_{\mu}(n)}$ (where $a$ is the lattice spacing and $1/g$ che coupling constant) we obtain:
$$
\begin{split}
\Pi_{\mu \nu} &\simeq \exp(iga[A_{\mu}(n)+A_{\nu}(n+\mu)-A_{\mu}(n+\nu)-A_{\nu}(n)])\\
&\simeq \exp(iga[A_{\mu}(n)+A_{\nu}(n)+a\partial_{\mu}A_{\nu}(n)-A_{\mu}(n)-a\partial_{\nu}A_{\mu}(n)-A_{\nu}(n)+\mathcal{O}(a^2)])\\
&\simeq \exp(iga^2[F_{\mu \nu} + \mathcal{O}(a)])\\
&\simeq 1 + iga^2[F_{\mu \nu} + \mathcal{O}(a)]-\frac{1}{2}g^2a^4F_{\mu \nu}^2+\mathcal{O}(a^5)
\end{split}
$$
so we can write the discrete action as:
$$
S_E = \beta \sum_n[1-\mathrm{Re}(\Pi_{12}(n)]\simeq \beta a^2g^2 \sum_n \frac{a^2}{2} F^2_{12}(n) \simeq \beta a^2 g^2 \int d^2x \frac{1}{2} F^2_{12}
$$
so $\beta = 1/(a^2g^2)$ is the parameter of our simulation. The continuum limit is $\beta \to \infty$ with the constrain : $\frac{N_sN_t}{\beta}$ = costant (that is the volume). In our simulation we consider $T=0$ case so $N_s = N_t$.
The distribution to sampling is:
$$
\mathcal{P}(U_{\mu}(n)) \propto \exp(\beta \mathrm{Re}(U_{\mu}(n) F^*_{\mu}(n)))
$$
Where $F_{\mu}(n)$ is called staple:
$$F_{\mu}(n) = \sum_{\nu \neq \mu} U_{\nu}(n)U_{\mu}(n+\mu)U^*_{\nu}(n+\mu)+U^*_{\nu}(n-\nu)U_{\mu}(n-\mu)U_{\nu}(n-\nu+\mu)$$
The observable to be measured is the topological charge, defined as:
$$
Q = \frac{1}{2 \pi} \sum_n \arg(\Pi_{12}(n))
$$
And the topological susceptibility:
$$
\chi = \frac{\langle Q^2 \rangle - \langle Q \rangle^2}{V}=\frac{\langle Q^2 \rangle - \langle Q \rangle^2}{N_sN_ta^2}=\frac{g^2}{4 \pi^2}
$$
So the dimensionless quantity measured is:
$$
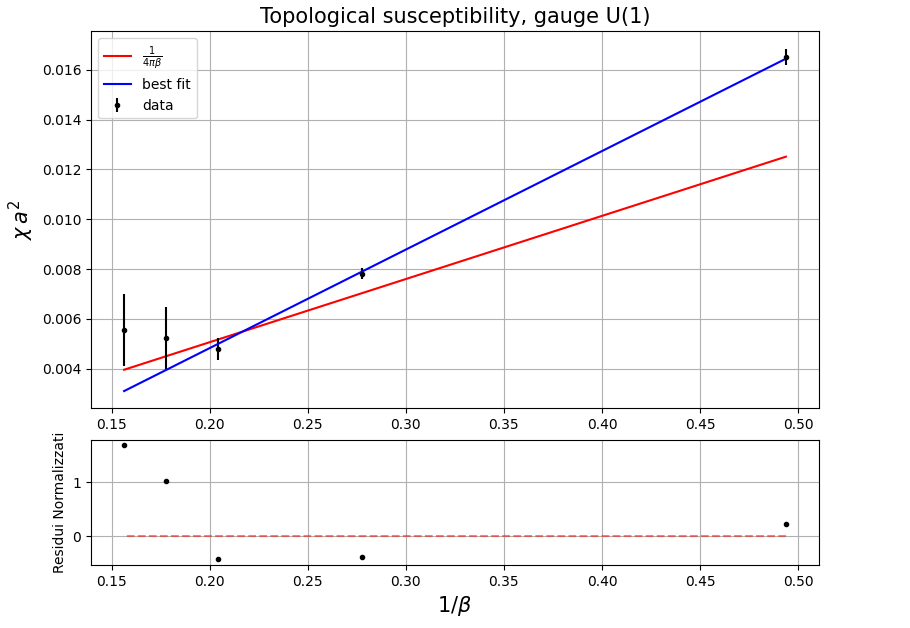
a^2 \chi = \frac{1}{4 \pi^2 \beta}
$$
Just by way of exposition, we report a small plot: