FlyingWorkshop / AutoDiff

Exploring automatic differentiation!

AutoDiff

The goal of this project is to be a stepping stone toward building a transformer from scratch (i.e., without TensorFlow or PyTorch). In order to circumvent both APIs, we have to understand what they are used for. Both libraries help streamline the construction of neural networks by making layers, regularizers, activations, etc. all seamlessly integrate together with fully-optimized library code. One of the particular advantages of using these libraries is not having to compute the gradient of loss function by hand. Before these libraries became popular (and although it was common in other fields outside of machine learning), it was common for researchers to painstakingly derive analytic solutions or approximations to their loss functions by hand before coding their models. Automatic differentiation (AD) alleviates the need to compute these tiresome derivatives using some clever techniques that we explore below, but before we can understand what AD is, we must understand what it isn't and what alternatives it supplants.

Numerical Differentiation

Recall the limit definition of the derivative: $f'(x) = \lim_{h \to 0}\frac{f(x+h) - f(x)}{h}$. It follows that we can approximate the derivative if we fix a small $h$. While this definition is perfect in theory, in practice dividing by a small $h$ on a computer leads to numerical errors and dividing by a large $h$ gives a bad approximation.

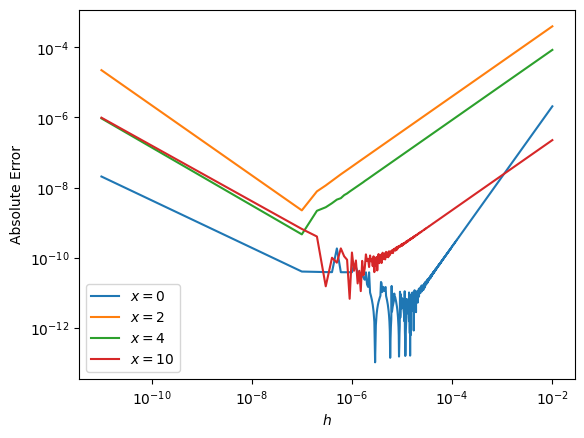
Below, we can see how the error changes with $h$. In this example, I used the sigmoid function and its derivative.

Numerical Errors: Rounding and Truncation

Rounding Errors: computers are limited in how they represent numbers

• magnitude: there are upper and lower bounds on what numbers computers can represent
• precision: not all numbers can be represented exactly

Truncation Errors: errors that result from the use of an approximation rather than an exact expression

(Source: MAE 4020/5020)

Automatic Differentiation

Forward Mode

Operator Overloading

Aside: Computational Graphs

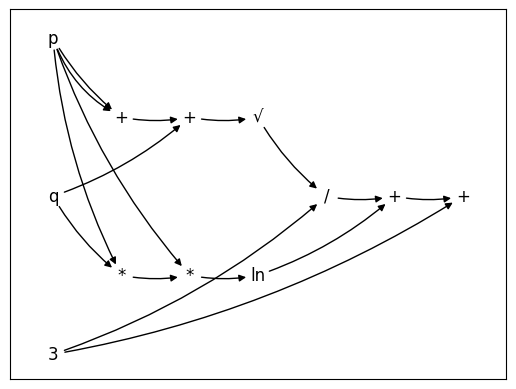
I implemented a custom computational graph engine as a sidequest. Here we see the computational graph (CG) for the equation $\sqrt{p + p + q} / 3 + \ln(p(pq)) + 3$. The graph is produced by overwriting python operators for a custom class that maintains a topologically-ordered directed multigraph.

import compgraph as cg

p = cg.Variable("p")
q = cg.Variable("q")
k = cg.Variable(3)
expression = cg.sqrt(p + p + q) / k + cg.ln(p * (p * q)) + k
expression.graph()

Compiler Stuff

Reverse mode

Back Prop