作者: 冯子嘉 2022012887
日期:2023.8.13
文件说明:
本项目实现了全光神经网络的仿真,在 MNIST 上最高达到了 97% 的正确率(当然是加了一个现实中根本不可能实现的非线性)
train 文件夹用于训练,predict 用于预测。
本文档中详述了原理及实现过程,建议先阅读项目文档再点进 train 与 predict 文件夹。项目文档中涉及的源代码主要蕴含在 train 文件夹中。
train 与 predict 文件夹内均有 README.txt 文件,建议查看后运行文件。
literature 是本项目的参考文献,可以对照项目文档最后的 reference 查看。
如果需要预处理完成之后的数据,可以联系作者。
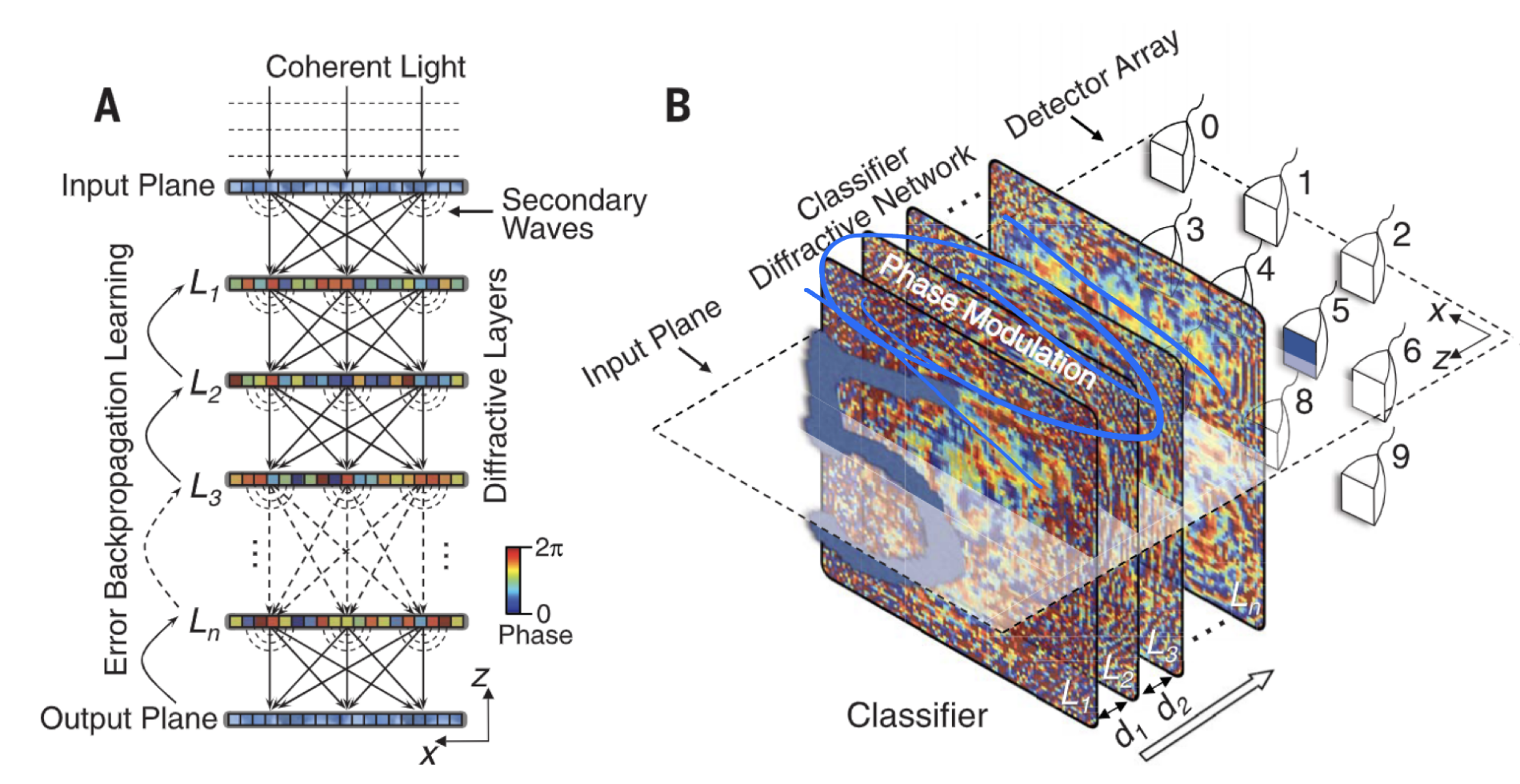
经典神经网络的架构人们已经耳熟能详。神经网络多基于GPU平台进行训练和推断。在Lin etc.的论文中,他们提出了一种基于光的衍射与相位调制的新型神经网络架构
本项目使用 Python + Pytorch 对全光神经网络进行仿真,并应用于MNIST手写数字识别中,通过调参取得了
本项目主要参考论文 All-optical machine learning using diffractive deep neural networks。预处理及训练代码请参考 source 文件夹中的内容,预测请参考 model 文件夹中的内容。
该网络的基本架构由三种 layer 组成,分别为:主管光波的空间自由传播的传播层 propagation_layer、进行光的相位与振幅调制的调制层 modulation_layer、以及最终实现预测的成像层 imaging_layer。
训练过程分为前向传播与反向传播,推断过程前向传播即可完成。
在前向传播中,该网络完整地模拟了光的物理传播过程。
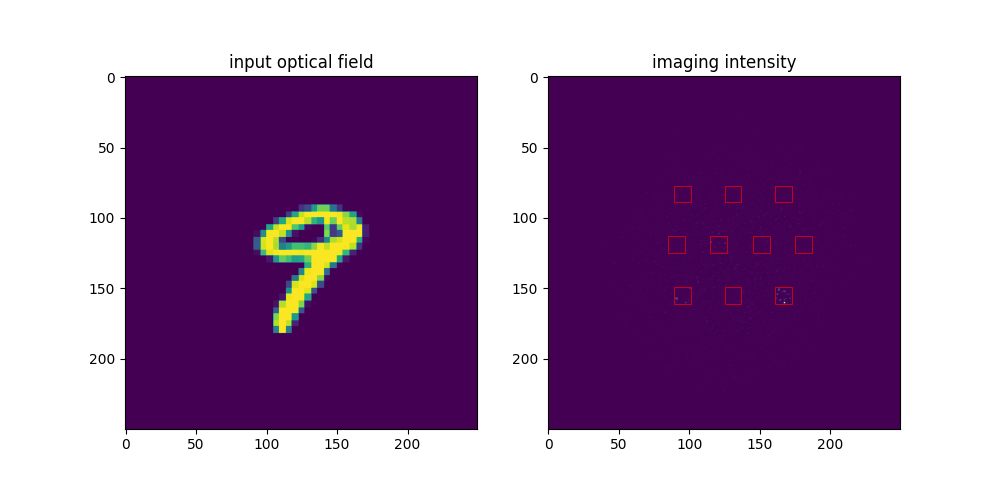
首先由一束相干光打入镂空的数字获得入射光场(input plane),接下来光在自由空间中传播,由菲涅尔衍射决定。在光传播的等间隔处加入了相位与振幅调制片(L1, L2...)。最后的成像屏中有十个方块,每个代表一个数字,squares中所获光强最大的一个即为全光神经网络的预测结果。
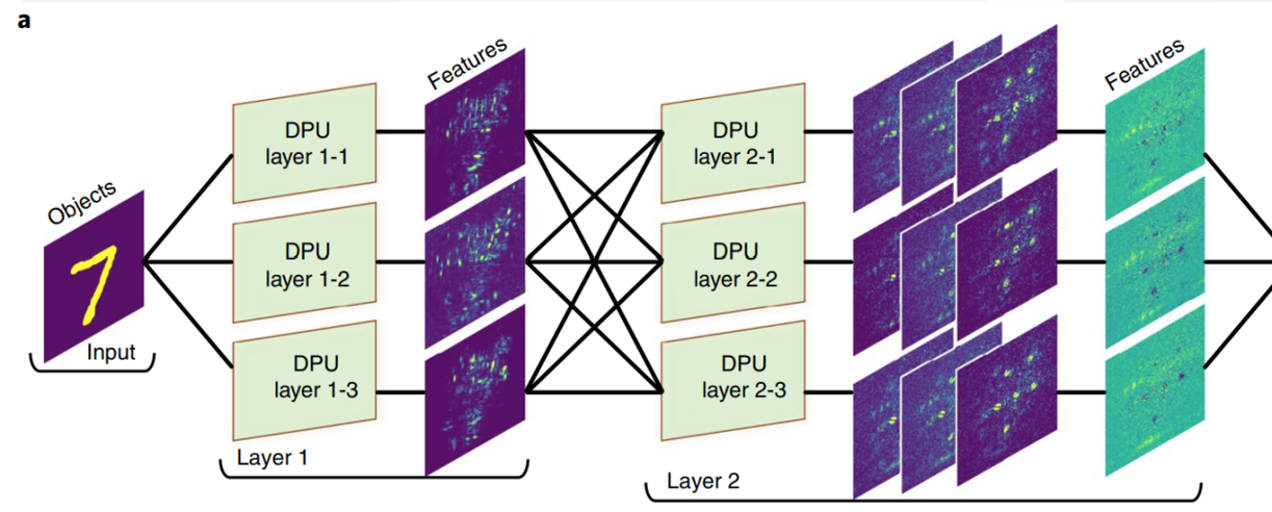
架构在下图中展现1 :
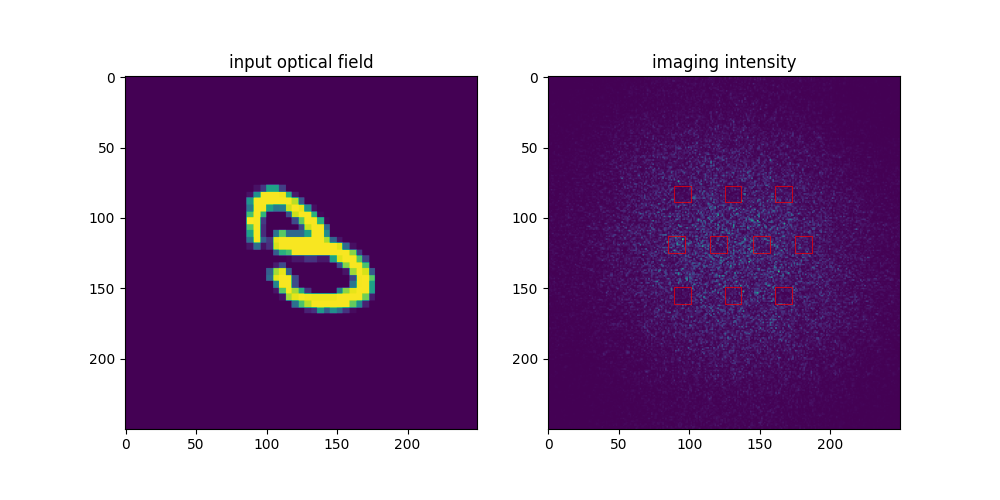
最终实现的效果如下所示。
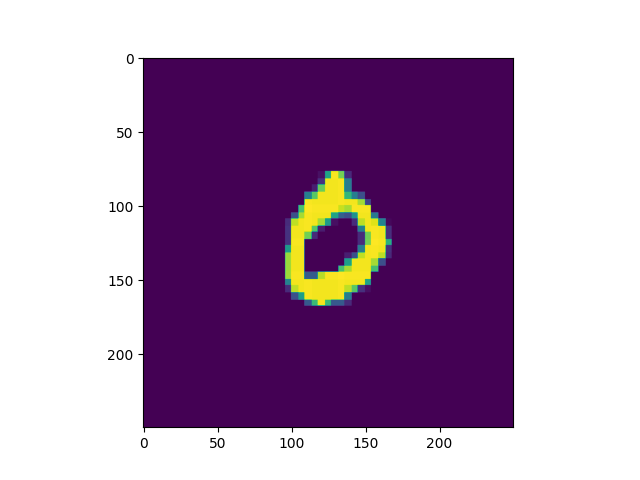 |
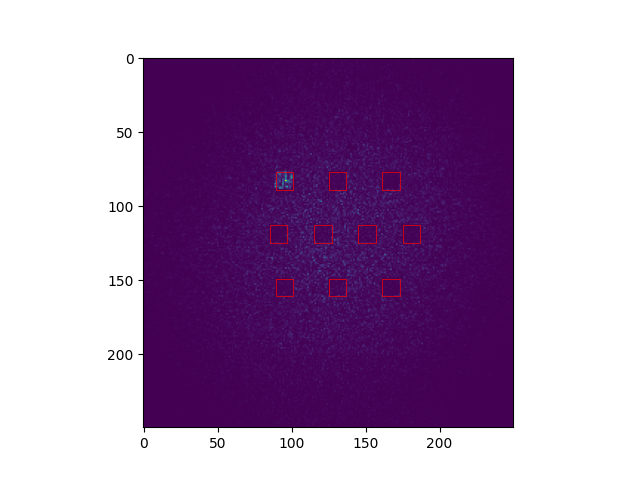 |
|---|---|
| 入射光场分布 | 成像光强分布 |
可以看到第一个square中的光强明显大于其余几个方块,因此0即为该神经网络的预测结果。
modulation_layer 中的相位与振幅调制片是网络中唯一的learnable parameter, 它们控制着光的传播。其更新使用梯度下降法完成。最终的调制片示例如下:
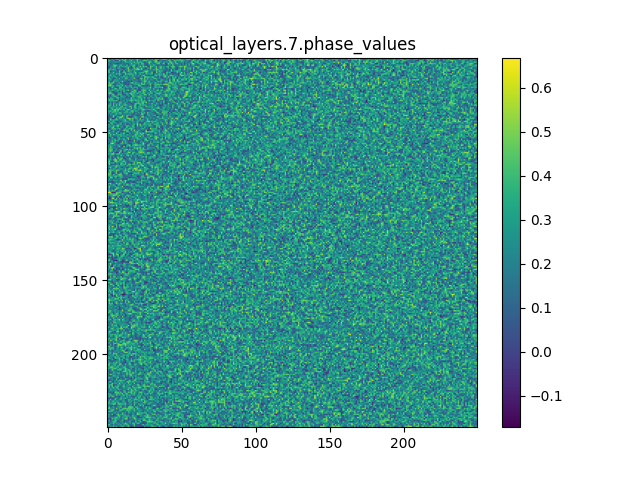 |
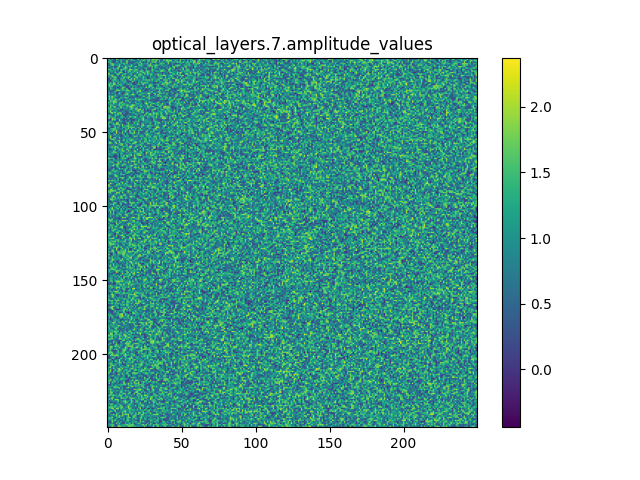 |
|---|---|
| 相位调制 | 振幅调制 |
使用vscode ssh连接精仪科协服务器进行训练。
软件环境: torch '2.0.1+cu117' + numpy '1.23.5'
硬件环境: NVIDIA GeForce RTX 3090(精仪科协服务器)
数据集: MNIST 手写数字识别
本部分的相关代码在 train.py, onn_am.py, layer_show.py中。第一个代码是训练的核心代码,第二个代码只含有optical network,第三个代码展示了传播层和调制层的工作。
作者自己写的 OpticalNetwork 类继承自 torch.nn。其实现可以单独参照 onn_am.py。类中有三种层:传播层 propagation_layer、调制层 modulation_layer 和成像层 imaging_layer。
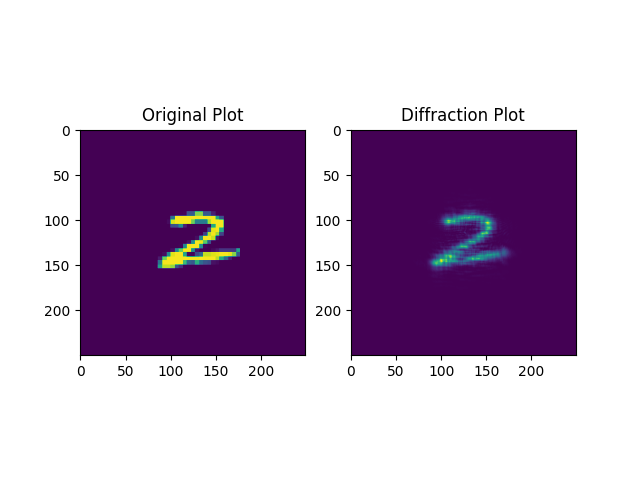
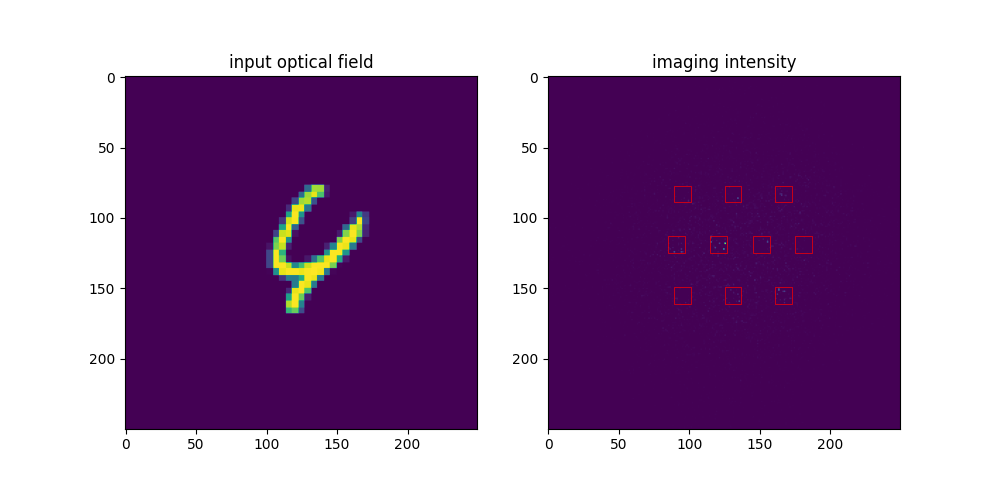
propagation_layer 模拟光在自由空间中传播一段距离 z 前后的光场变化。作者采用菲涅尔传递函数 (Transmittive Funtion, TF) 法,参照 Computational Fourier Optics 的实现完成 propTF() 函数。经过一个传播层的结果如下所示。
可以看到自由空间传播的卷积效果对图象造成了一定模糊。
菲涅尔传递函数方法可以用角谱法在傍轴近似下保留二阶小量得到。其原理详见 Goodman: Introduction to Fourier Optics, Edition 4th。其实现详见训练所用代码 train.py。
modulation_layer 主要引入相位和振幅调制片。调制片与采样空间有着同样的 size。作为唯一可调参数的layer,在定义完各个层之后,相位与振幅调制的参数可以直接调用 loss.backward() 完成计算,使用 optimizer.step() 完成更新。
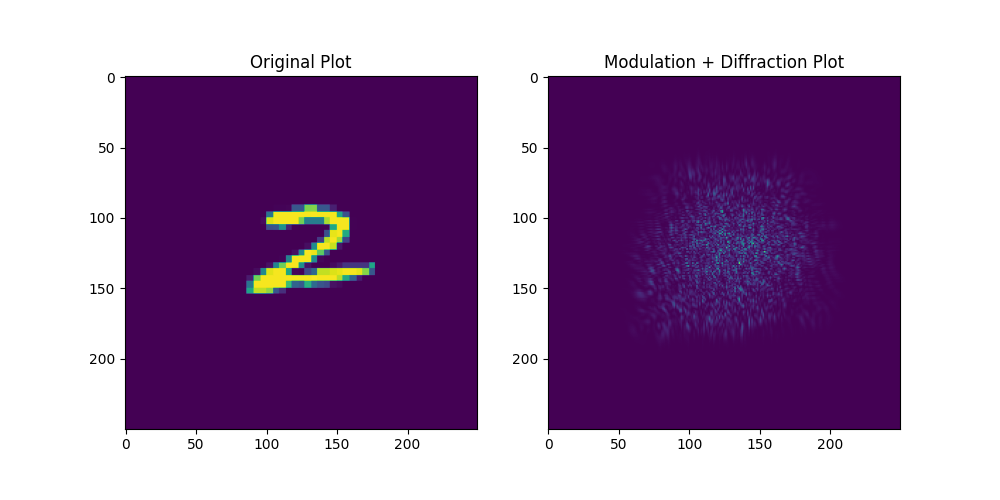
以下是进行随机相位调制之后再传播
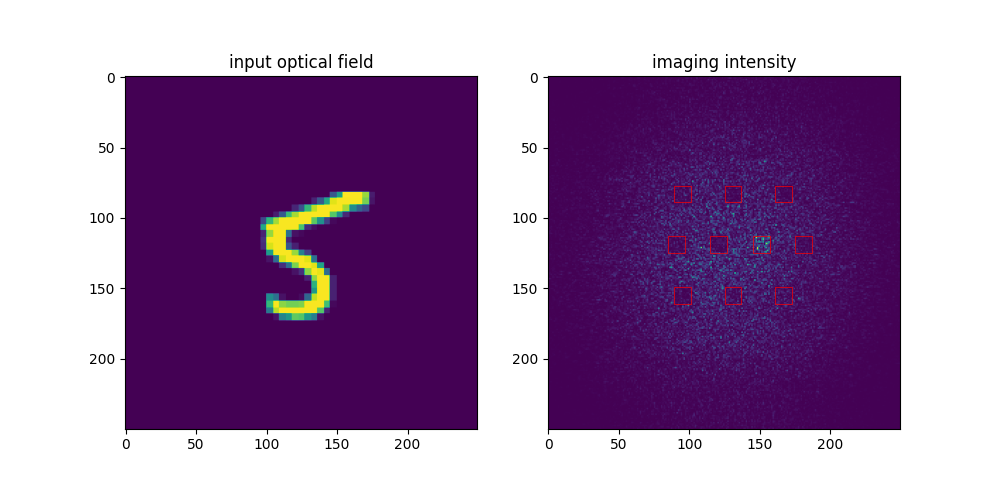
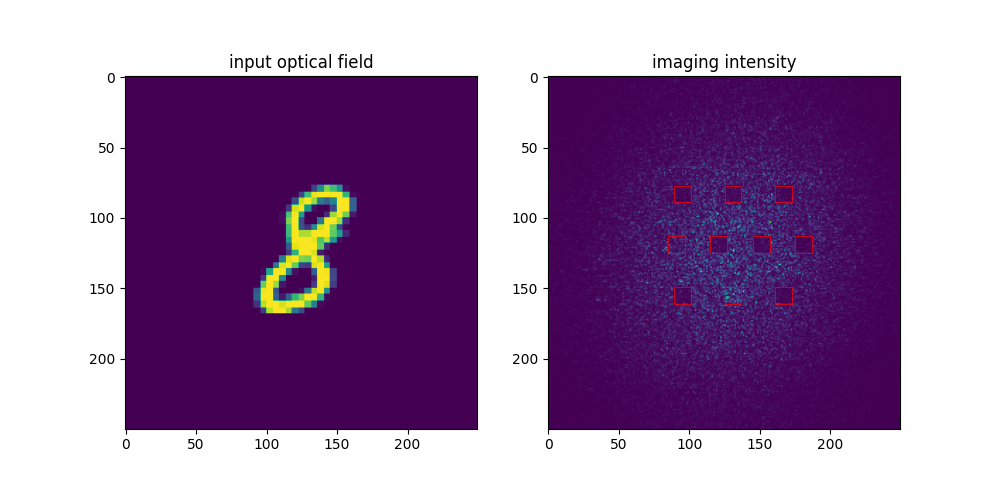
imaging_layer 完成成像和输出的任务。在计算总的光强后,imaging_layer 会对每一个方块中的光强大小进行统计并进行归一化,输出一个 dim = 10 的tensor,光强最大的即为预测结果。
举例而言,在下右图中,其对应的tensor为:
0.1584, 0.1126, 0.1083, 0.1370, 0.1285, 0.8973, 0.1393, 0.1145, 0.2016, 0.1920
可以明显看到 tensor[5] 的数值最大,因而5就是我们的预测结果。
需要特别注意的是:imaging_layer 中归一化操作不能就地完成,否则梯度计算会出错,需要新定义一个 value_ 数组再return。
最终的模型由
组成。
模型的损失函数使用 MSELoss(),参数初始化方法选择 kaiming_uniform_ 或uniform_,优化器选用 Adam。
这里是固定参数,此处只列出参数及其代表的含义,其选择原因见"参数的选择原因"
光学参数
M = N = 250 # sampling count on each axis
lmbda = 0.5e-6 # wavelength of coherent light
L = 0.2 # the area to be illuminated
w = 0.051 # the half-width of the light transmission area
z = 100 # the propagation distance in free space
在使用全部MNIST数据进行训练时的神经网络参数为:
learning_rate = 0.003
epochs = 6
batch_size = 128
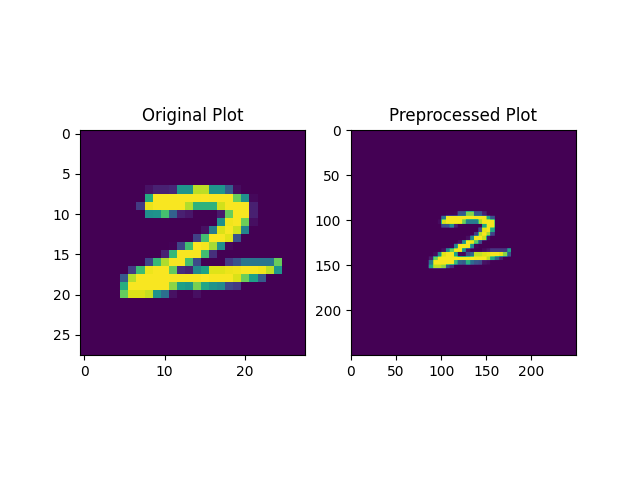
预处理的相关代码在 prepro.py以及 prepro_label.py 中。其核心在于将图片重新采样,将其大小限制在
label的预处理在于把一个数字扩展成一个 dim = 10 的数组。若label =
预处理完成后保存为npy文件,便于在不同设备上的转移与读取。
小批量数据的读取可以直接通过 np.load() 完成,但MNIST的训练数据超出了GPU内存的限制,必须通过dataloader完成。具体代码参照 train.py or train_am.py。
以下结果是没有加入振幅调制,只有振幅调制的结果。加入振幅调制的结果将在下一板块"模型调优"进行讨论。
笔者一开始使用MNIST的前
若使用参数
learning_rate = 0.003
epochs = 20
batch_size = 128
一次训练及测试所需的时间大约为50s,方便调参。以下是其中一次的输出结果,其权重保存到了weights_small.pt中
Using cuda device
Epoch [1/20], Training Loss: 0.1198, Training Accuracy: 70.10%,
...
Epoch [20/20], Training Loss: 0.0255, Training Accuracy: 95.90%,
Validation Loss: 0.0397, Validation Accuracy: 87.50%
Test Accuracy: 90.50%
在小批次数据集上,笔者在测试集上最高达到过92.5%的正确率。平均正确率约为
笔者后来使用MNIST的全部进行训练与测试,也即 $ \rm 50000 \times train + 10000 \times validation + 10000 \times test$。使用参数
learning_rate = 0.003
epochs = 6
batch_size = 128
一次训练及测试的结果大约为40min。以下是一次输出的结果,其权重保存到了weights_large.pt中。
Epoch [6/6], Training Loss: 0.0243, Training Accuracy: 92.86%,
Validation Loss: 0.0225, Validation Accuracy: 93.64%
Test Accuracy: 92.65%
在大批次数据集上的结果,validation set中的正确率超过
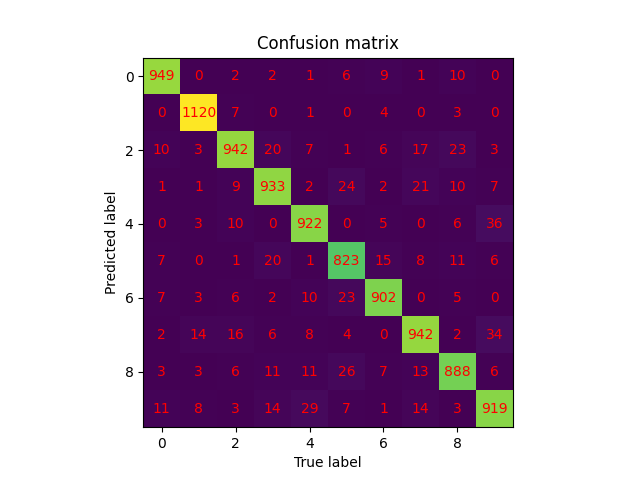
我们列出大批量数据和小批量数据的 confusion_matrix 以作对比。
| 大批量数据 | 小批量数据 |
|---|---|
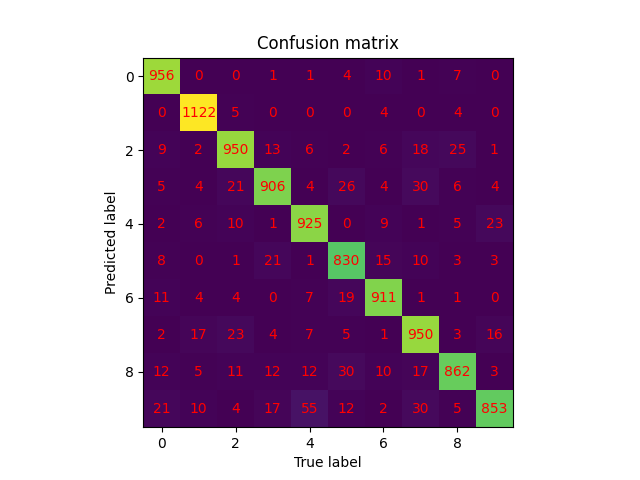 |
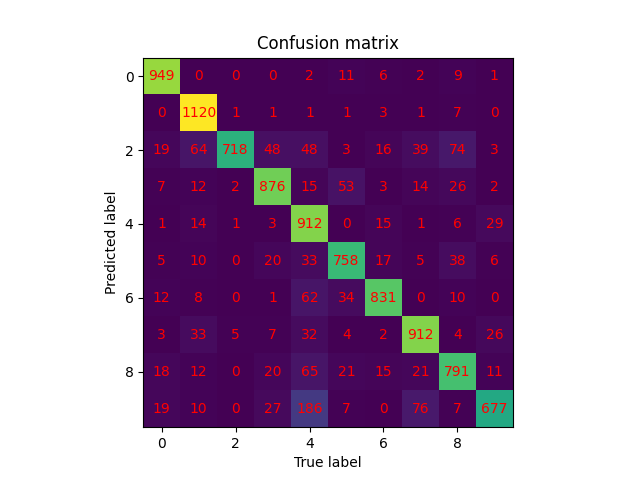 |
我们通过列出模型归一化之后的输出结果 output && 入射光场与最终成像光强的对比展示模型的预测表现。
- 若没有振幅调制
[[0.1320, 0.1467, 0.2757, 0.6138, 0.3394, 0.4097, 0.3318, 0.1327, 0.2697, 0.1574]]
[[0.0817, 0.1322, 0.1069, 0.3428, 0.1222, 0.1302, 0.0683, 0.0961, 0.8899, 0.0956]]
- 若加入振幅调制:
[[0.0813, 0.1146, 0.2029, 0.3622, 0.7564, 0.1387, 0.0544, 0.0728, 0.2183, 0.4007]]
[[0.0088, 0.0123, 0.0308, 0.0656, 0.1741, 0.0357, 0.0339, 0.3735, 0.0609, 0.9047]]
对比图在 predict.py 与 predict_am.py 中生成。
step1: 预处理
运行 prepro.py & prepro_label.py,生成预处理之后的光场分布并保存为npy文件。注意按照 prepro.py 文件中的提示修改参数。
step2: 模型训练
这里我们提供两种模型:large.py, large_am.py。前者只有相位调制,后者引入了振幅与相位调制。更改文件名与prepro.py中生成的文件名一致。
step3: 模型预测
根据上一步训练的模型种类运行 predict.py 或 predict_am.py。更改 line 157中的
u0 = test_data_transposed[17] 为你所想要运行的数据。将会生成最终的对比图,如上一板块所示
这里我们主要讨论模型架构的优化,参数的优化详见下一章:选择依据。本版块提出四种优化方法:增加层数、加入振幅调制、增加非线性激活函数和改变传播距离。
调整架构,小批次数据全部采用参数lr = 0.003, epoch = 20. 相位初始化使用$(0,4\pi)$中的均匀分布。大批次数据全部采用参数lr = 0.003, epoch = 6. 相位初始化使用$(0,4\pi)$中的均匀分布
调整架构中最显而易见的方法就是增加层数。在小批量数据上的实验结果如下所示:
| 层数 | 正确率 |
|---|---|
| 1 | 8.5% |
| 2 | 63.5% |
| 3 | 87.5% |
| 4 | 89.0% |
| 5 | 90.5% |
| 8 | 92.0% |
| 12 | 92.5% |
可以发现增加层数可以显著增加正确率,但在现实生活中这样更难以制作投入使用,且制造工艺带来的误差可能会增加。5-8层应该是较为合适且折衷的选择。
相关代码在所有以 am 结尾的文件中。所有以 am 结尾的文件都代表着有 amplitude modulation。
其次是在相位调制之上加入振幅调制。
以下是在MNIST全集上的训练结果。经过对比,加入振幅调制可以较为显著地提高正确率,且没有增加很多训练时间。不过在现实应用中又增加了复杂度。
| 有振幅调制 | 无振幅调制 | |
|---|---|---|
| test | 93.4% | 92.5% |
| validaiton | 93.9% | 93.5% |
Epoch [6/6], Training Loss: 0.0203, Training Accuracy: 93.64%,
Validation Loss: 0.0191, Validation Accuracy: 93.86%
Test Accuracy: 93.40%
| 有振幅调制 | 无振幅调制 |
|---|---|
 |
 |
虽然本模型在传播过程 propagation_layer 中自然引入了一定的非线性因素,但整体实现仍然依赖线性叠加。引入非线性激活函数将对模型产生积极影响。因此本文引入complex ReLU function crelumodulation 的光场进行调节,最终可以达到超过
def crelu(x):
return torch.relu(x.real) + j * torch.relu(x.imag)特别需要注意:引入 crelu 后可能使得最后imaging时结果通通为0,若加之以浮点误差则可能使得归一化中的范数计算 norm 出现问题。这时我们可以通过给 norm 一个底线来解决这一问题。代码详见 large_relu.py,将 norm 改为 norm_nonzero 即可。
def norm_nonzero(x):
# Add a small constant to ensure non-negativity and avoid numerical instability
epsilon = 1e-10
return torch.sqrt(torch.clamp(torch.dot(x, x), min=epsilon))| 引入relu | 不引入relu | |
|---|---|---|
| test | 96.98% | 92.5% |
| validaiton | 97.01% | 93.5% |
Epoch [6/6], Training Loss: 0.0046, Training Accuracy: 98.80%,
Validation Loss: 0.0059, Validation Accuracy: 97.01%
Test Accuracy: 96.98%
值得记录的是,使用 csigmoid 并不能达到与之相仿佛的效果。说明 sigmoid 作用在complex value上不能通过简单地应用到实部与虚部来完成。
Epoch [1/6], Training Loss: 0.1367, Training Accuracy: 11.36%,
Validation Loss: 0.1367, Validation Accuracy: 10.64%
这一方法的最大弊端在于其物理实现的困难。目前尚难以找到适合便捷地引入complex activation function的光学介质。$^3$
相关代码在 changez.py 中。
该思路为改变z,使得z变成一个可以学习的参数。经过小批量数据上的测试,使用过大的学习率会导致z剧烈抖动,正确率在10%上下浮动,如左图;而学习率较小时z几乎不改变,如右图。因此这一改动被放弃。
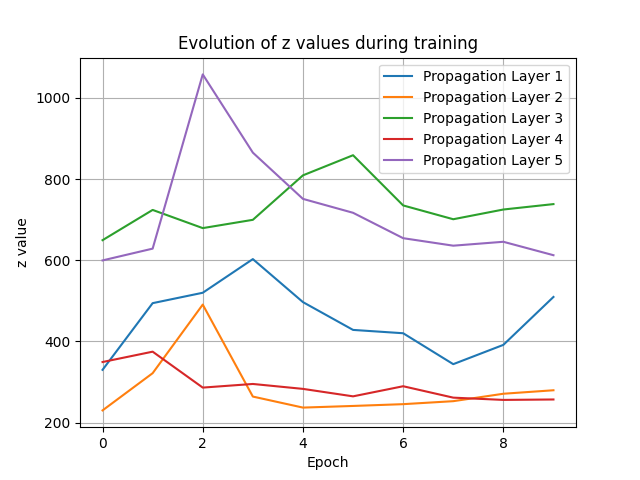 |
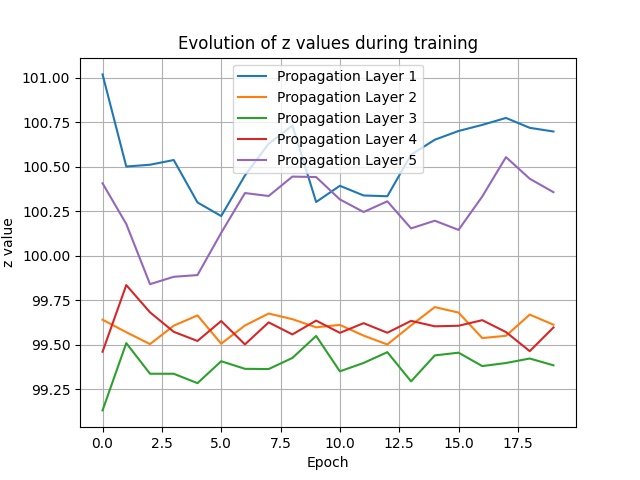 |
|---|---|
| lr = 20 | lr = 1 |
借鉴卷积神经网络共享权重和偏置的方式,结合到本项目中来的实现方式是增加几个平行的连接层。详情参见large_dn1n_final.py
这个训练实在是太慢了…跑了两次都没跑完。效果也没有太好,说明在该非线性度下,我们已经达到了极致。
示意图:(参照Zhou etc. 2021文章,reconfigurable ONN的灵感)
weights_large_dn1n_feature20.pt
Epoch [4/5], Training Loss: 0.0208, Training Accuracy: 93.37%,
Validation Loss: 0.0191, Validation Accuracy: 94.05%
Epoch [5/5], Training Loss: 0.0205, Training Accuracy: 93.73%,
Validation Loss: 0.0187, Validation Accuracy: 93.91%
Test Accuracy: 93.29%
结果:
| validation set | test set | |
|---|---|---|
| 2 epoches + crelu | 96.95% | 96.91% |
| 5 epoches | 93.91% | 93.29% |
使用远距离传输修正的propagation_ASM.py中的方法,训练代码在provided_large.py中。效果没有显著差别。
预测在predict_inco.py中,其中inco代表incoherent,非相干。
训练在large_inco.py中。权重也都公开了。效果上,非相干最好之后58%左右。根据林星老师的看法,这是因为非相干光没有负值运算。
M = N = 250 # sampling count on each axis
lmbda = 0.5e-6 # wavelength of coherent light
L = 0.2 # the area to be illuminated
w = 0.051 # the half-width of the light transmission area
z = 100 # the propagation distance in free space
参数
这边我们的
参数 propTF 方法在较小的
神经网络参数的调整主要依赖实验结果。
特别值得一提的是,论文中给出的
lr 不宜过高或过低。在MNIST全集的条件下,$\rm test_accuracy$ 与 $\rm validation_accuracy $ 基本持平,暂时没有观察到过拟合的现象,说明 lr 本身相对较大,起到了一定规范化的作用。