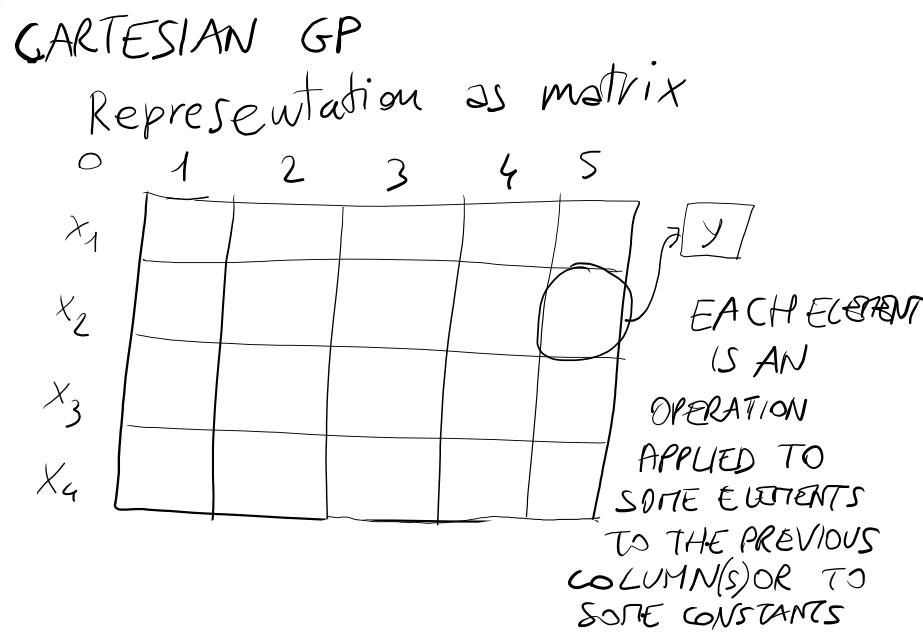
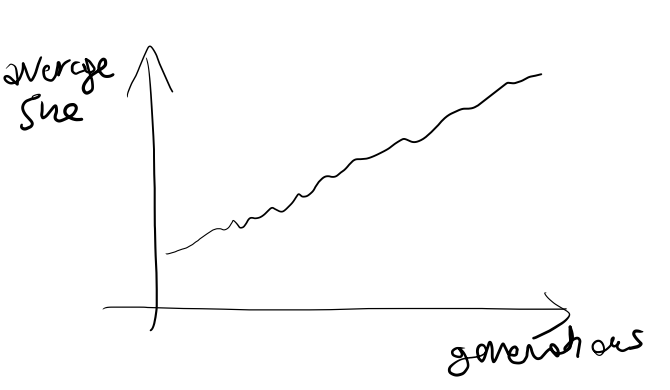
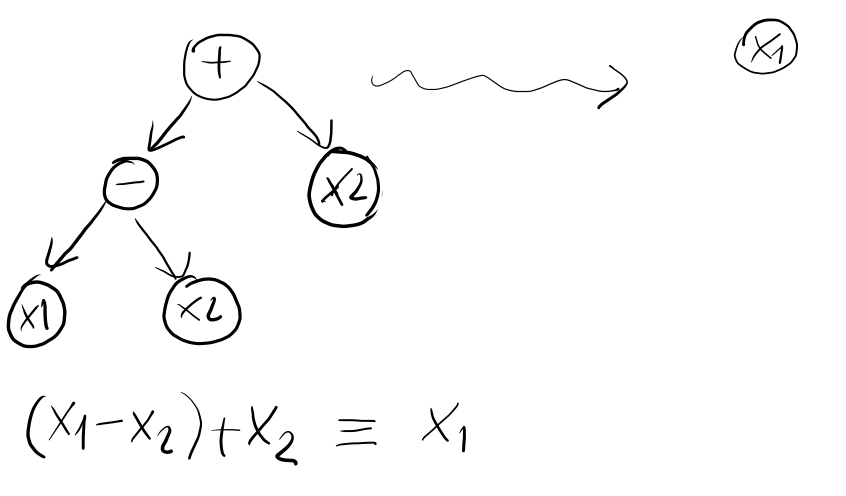
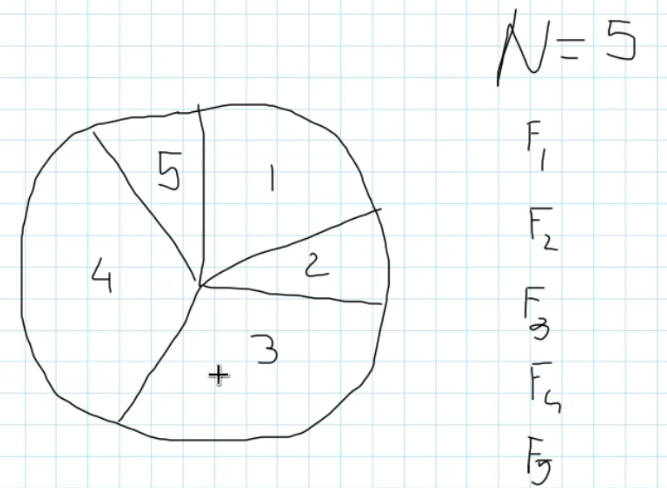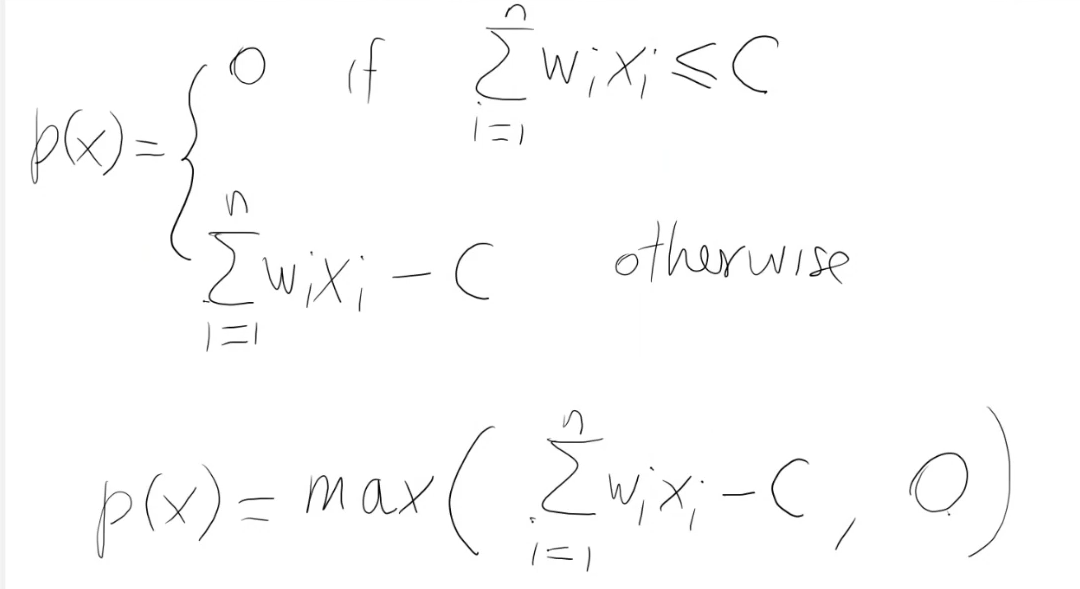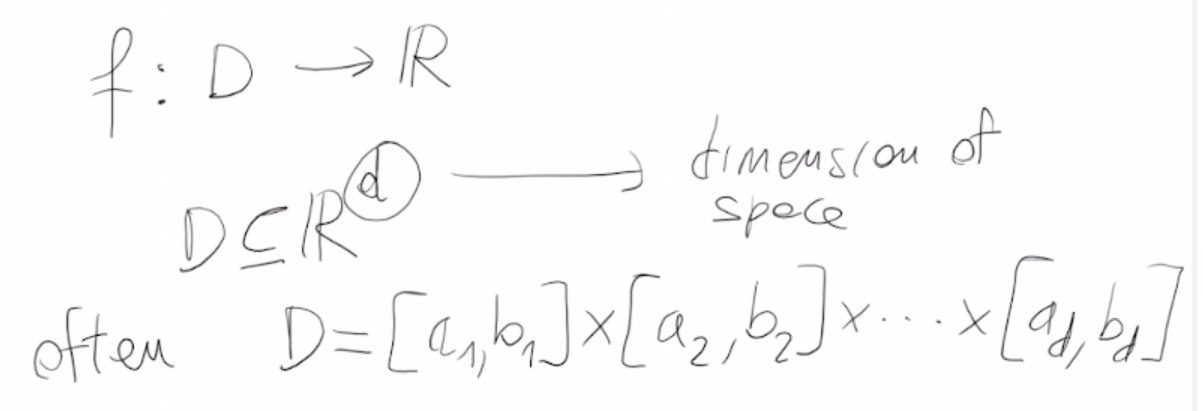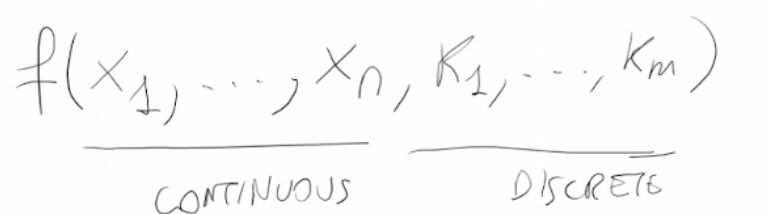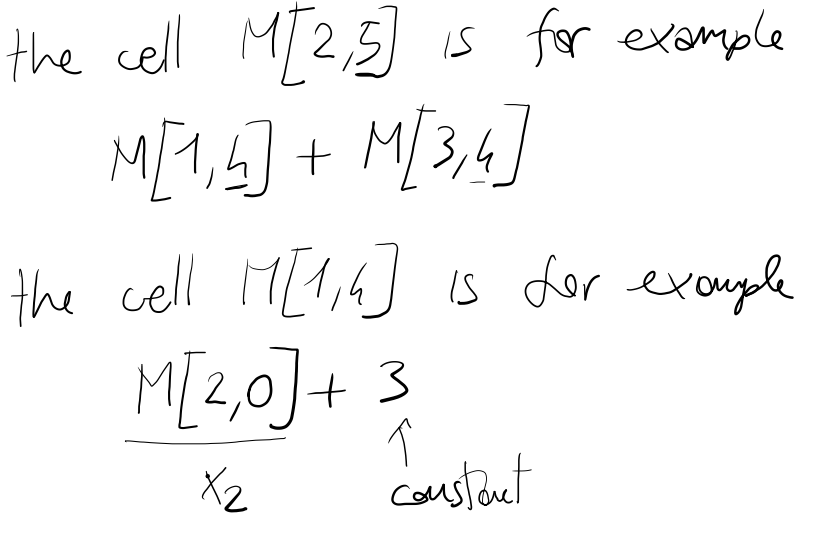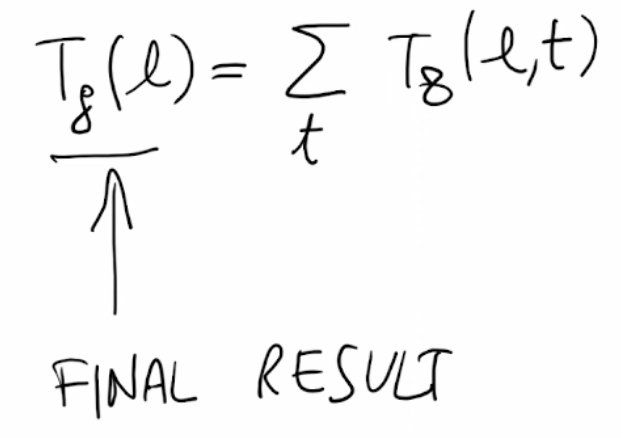- Algoritmi Genetici
- Problemi Vincolati
- Swarm Intelligence
-
Esame (2 parti):
- Progetto
- Implementazione di qualche algoritmo (linguaggio di programmazione a scelta):
- algoritmi evolutivi
- sistema fuzzy
- sistema probabilistico
- libreria per velocizzare alcune cose e quindi applicarlo ad un problema effettivo
- Analisi di un articolo di ricerca (solo per studenti che hanno un interesse scientifico (tesi, dottorato ecc...))
- Implementazione di qualche algoritmo (linguaggio di programmazione a scelta):
- Orale:
- domande sul programma
- presentazione progetto
- Progetto
-
Materiale:
- libri di testo (qualche capitolo indicato dal prof)
È una parte dell'Intelligenza Artificiale che comprende alcuni strumenti che si utilizzano in essa. Argomenti principali:
- Reti neurali (già trattato nel corso di Machine Learning e quindi non lo trattiamo)
- Sono lo strumento più famoso ma non l'unico che può essere utilizzato nelle applicazioni di intelligenza artificiale.
- Algoritmi evolutivi
- Ne fanno parte le Metaeuristiche.
- Sono uno strumento utilizzato per risolvere i problemi di ottimizzazione particolarmente difficili.
Esempi di problemi di ottimizzazione:- Il training delle reti neurali;
- Clustering;
- Costruzione degli alberi decisionali ecc...
- Uno dei problemi di ottimizzazione più famosi è il "Problema del commesso viaggiatore".
- Logica Fuzzy
- È uno strumento che serve per rappresentare concetti vaghi.
- Esempio di concetto vago: La temperatura è alta (non ti dico esattamente una soglia secondo cui la temperatura inizia ad essere alta o meno). Esiste un confine sfumato tra alto e non alto.
- È uno strumento che serve per rappresentare concetti vaghi.
- Modelli probabilistici
- Usati per rappresentare l'incertezza.
- Esempio: La probabilità che il paziente abbia una determinata malattia è 0.25 , come posso usare questa informazione all'interno di un sistema di AI? I modelli probabilistici consentono di trattare questo tipo di informazioni (probabilistiche).
- Usati per rappresentare l'incertezza.
Gli ultimi 3 argomenti completano il bagaglio degli strumenti che possono essere utilizzati nell'AI.
Esistono 2 livelli nelle Intelligenze Artificiali (e da questo anche 2 modi per approcciare l'AI):
- Livello simbolico (Intelligenza Artificiale classica)
- Logica proposizionale/booleana (algoritmi di ricerca come: BFS, DFS, A*, planning ecc...)
- Opera ad alto livello: l'informazione è codificata in modo simbolico (rappresentazione simbolica).
- Logica proposizionale/booleana (algoritmi di ricerca come: BFS, DFS, A*, planning ecc...)
- Livello subsimbolico (Intelligenza Artificiale "moderna")
- Ad esempio il riconoscimento delle immagini funziona meglio a livello subsimbolico (lavoro sui pixel e non sulle forme geometriche individuabili nelle immagini, come viene invece fatto a livello simbolico).
- Rappresentazione numerica invece della rapresentazione logica/discreta (esempio nel riconoscimento delle immagini sopra).
Molti problemi di ottimizzazione sono computazionalmente difficili (Es: np-hard o peggio).
Breve cenno sul significato di NP: La classe di problemi NP comprende tutti quei problemi decisionali che, per trovare una soluzione su una macchina di Turing non deterministica, impiegano un tempo polinomiale. La classe NP prende il suo nome dall'abbreviazione di Nondeterministic Polynomial Time.
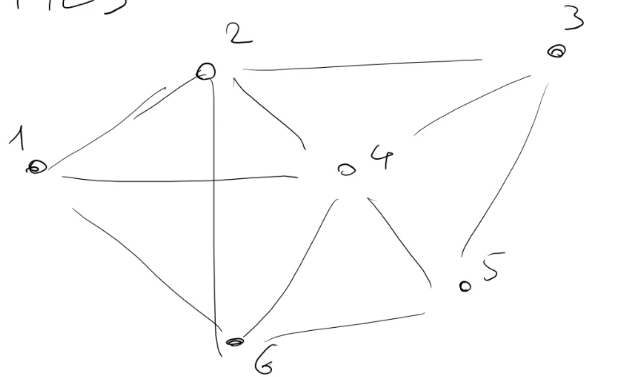
- n città
- Il grafo è solitamente completo (da ogni città posso andare ad ogni altra città) e può essere sia orientato che non orientato.
- Ho una matrice che rappresenta le distanze/costi:
- d(i,j) è la distanza tra la città i e la città j (o il costo per andare da i a j)
- Se il grafo è completo ogni entrata ha un numero reale
- Se non c'è collegamento tra i e j si può mettere che d(i,j) = infinito
Il problema TSP può essere:
-
simmetrico: d(i,j) = d(j,i)
$\forall$ (per ogni) i,j -
asimmetrico: d(i,j) != d(j,i)
$\exists$ (esistono) i e j per cui si verifica ciò (Esempio: città in salita e discesa).- euclideo: d(i,j) = distanza(posizione città i, posizione città j) -> distanza euclidea (non realistica, realistica solo se la terra fosse piatta).
Il TSP è NP-hard se visto come problema di ottimizzazione, oppure è NP-completo come problema decisionale.
Definizione.
Un problema di ottimizzazione è definito da:
- uno spazio di ricerca X
- una funzione obiettivo f: X -> R (non necessariamente sarà sempre R)
Lo scopo è trovare il valore x* appartenente a X tale che f(x*) sia minimo (o massimo)
Nel problema del commesso viaggiatore:
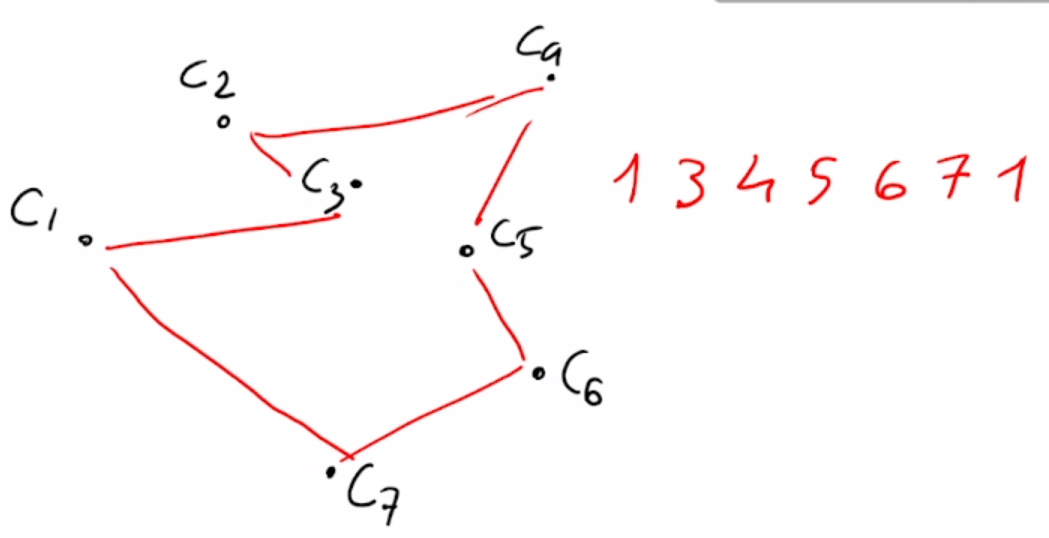
- X è l'insieme di tutti i cicli Hamiltoniani del grafo
- un ciclo Hamiltoniano è una sequenza di città che inizia da una città prestabilita c0, passa per tutte le città una sola volta e termina in c0.
Es: 1->3->4->2->6->5->1 (nel grafo di prima)
- un ciclo Hamiltoniano è una sequenza di città che inizia da una città prestabilita c0, passa per tutte le città una sola volta e termina in c0.
- La funzione obiettivo f è la distanza totale (o il costo) del ciclo Hamiltoniano.
f(1->3->4->2->6->5->1) = d(1,3) + ... + d(5,1)
- x* è il ciclo Hamiltoniano con la minima distanza totale.
Ciò lo rende un problema NP-hard.
- x* è il ciclo Hamiltoniano con la minima distanza totale.
Note:
- Trovare un ciclo Hamiltoniano è semplice se il grafo è completo.
- Computare f è facile (Calcolare f).
- La difficoltà sta nel trovare x*
X è l'insieme di tutte le permutazioni delle città (dei nodi del grafo) (con la prima città che deve essere rimessa anche in fondo).
In alcuni problemi anche generare un elemento di X può essere difficile (elemento di X = soluzione ammissibile).
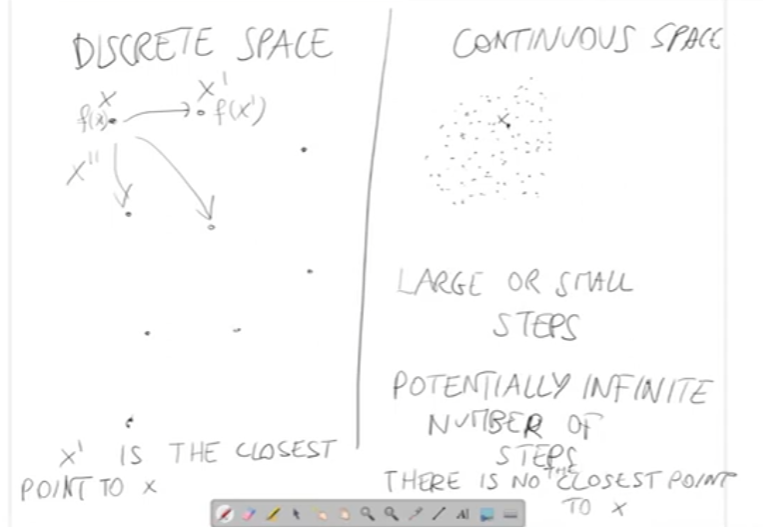
- Discreti (Es: TSP)
- Un problema di ottimizzazione è discreto quando X (spazio di ricerca) è un insieme finito.
- In un problema discreto ogni X(i) ha un dominio finito.
- Es: Se il grafo ha n città, ci sono (n-1)! cicli hamiltoniani.
- Continui
- X è un insieme infinito (Es: R o un intervallo)
- Lo spazio di ricerca è costituito da numeri reali, vettori di numeri reali, matrici di numeri reali ecc...
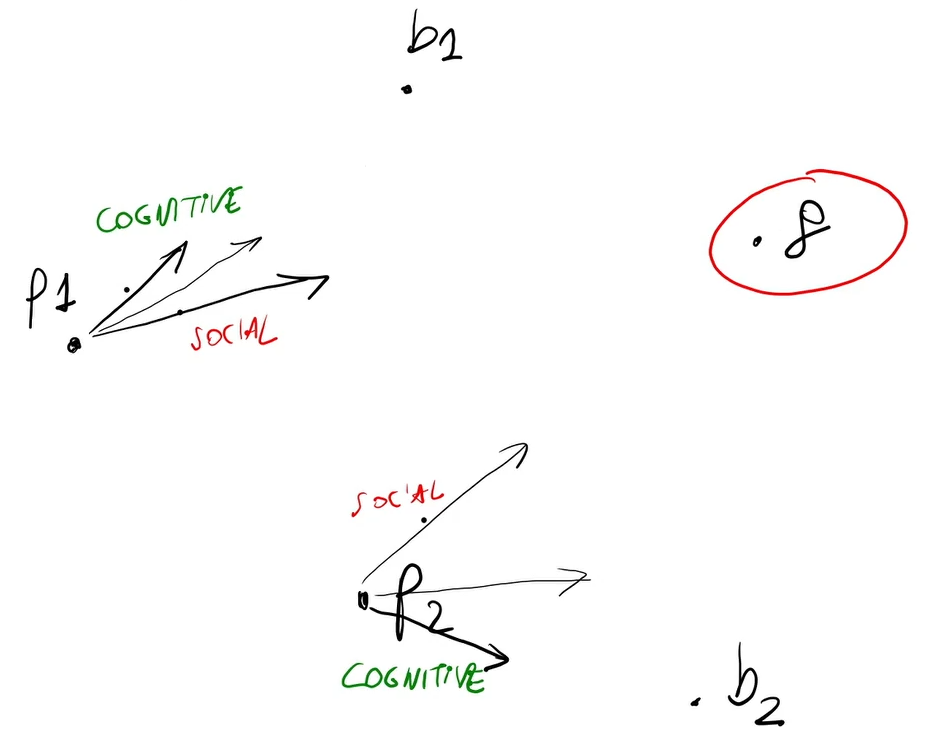
- Es: determinare la posizione di n punti in modo tale da minimizzare la somma complessiva delle distanze da un determinato punto fissato.
- In un problema continuo ogni X(i) ha un dominio infinito.
- ES: ho una città e devo mettere delle stazioni di ricarica. Le devo mettere in modo tale che sia minima la somma complessiva delle distanze delle varie città in modo tale che un veicolo non deve fare troppa strata per potersi ricaricare.
- X è un insieme infinito (Es: R o un intervallo)
Si distingue anche tra problemi di ottimizzazione con:
-
funzioni obiettivo lineari
- f(xi, ... , xn) =
$w_1$ $x_1$ +....+$w_n$ $x_n$ - Es: funzione problema dello zaino.
- f(xi, ... , xn) =
-
funzioni obiettivo non lineari
- f non è una combinazione lineare
$x_1$ , ... ,$x_n$
- f non è una combinazione lineare
Si hanno inoltre:
- problemi vincolati:
- X è ottenuto aggiungendo vincoli allo spazio di ricerca originale.
- Es: lo zaino è un problema vincolato. Senza vincoli lo zaino è senza limiti e si prenderbbero tutti gli oggetti, ottenendo il massimo valore. Il problema dello zaino classico è quello vincolato (ogni oggetto ha un valore e un peso e lo zaino ha un limite)
- X è quindi ristretto.
- X è ottenuto aggiungendo vincoli allo spazio di ricerca originale.
I problemi di ottimizzazione possono anche avere:
- una singola funzione obiettivo
- più funzioni obiettivo
- Es: TSP con tempo e carburante come funzioni obiettivo (che in questo caso sono addirittura in competizione).
Quali sono le possibili soluzioni algoritmiche per un problema di ottimizzazione combinatoria come TSP?
- Algoritmi esatti:
- Risolvono in maniera esatta il problema. Non sono comunque in grado di risolvere istanze medio-grandi.
- All'aumentare dell'istanza anche di poco, i tempi di calcolo crescono esponenzialmente. Perche gli algoritmi sono solitamente esponenziali, al massimo polinomiali.
- È possibile anche usare alcuni "universal solver". Ad esempio un SAT solver o MIP solver. Significa formulare il problema di ottimizzazione come un SAT o un mixed integer probgramming.
- Algoritmi Approssimati:
- Sono algoritmi studiati ad Hoc per il problema che trovano soluzioni sub-ottimali in tempo polinomiale. La soluzione trovata non è peggio di una certa quantità rispetto all’ottimo. Usano delle euristiche pensate appositamente per il problema.
- Approssimare il problema di ottimizzazione: utilizzare un algoritmo approssimato.
- Anziche trovare x* tale che f(x*) sia massimo o minimo, questi algoritmi trovano un x' tale che f(x') <= k * f(x*)
- Es: f(x*) = 300
x' ---> f(x') <= 2*300
Ovviamente minore è k e meglio è.
- Es: f(x*) = 300
- x' non è un minimo, è qualcosa che gli si avvicina ma quanto è lontano?
- Per ottenere bassi valori di k è richiesto maggiore tempo.
- Ci sono dei problemi di ottimizzazione in cui k non può essere scelto però. Non possono essere approssimati meglio di quel k.
- Anziche trovare x* tale che f(x*) sia massimo o minimo, questi algoritmi trovano un x' tale che f(x') <= k * f(x*)
- Metaeuristiche:
- Trovano soluzioni sub-ottimali in tempo polinomiale. Non danno la garanzia di un limite per la soluzione, ma il vantaggio è che lo schema si può applicare con opportuni cambiamenti a molti problemi di natura diversa. Questi metodi fanno poche o nessuna ipotesi sul problema da ottimizzare e possono cercare spazi molto ampi di soluzioni candidate.
- Una metaeuristica è un algoritmo che da una soluzione del problema, la quale non è necessariamente ottima ma potrebbe essere molto buona, ottenuta soprattuto in un tempo ragionevole. Non c'è nessuna garanzia su quanto è buona la soluzione e non riesco a stimarlo. Questo è il prezzo da pagare per utilizzare una metaeuristica.
- Metaeuristica significa che la stessa
tecnicapuò essere usata (adattandola) a un'ampia gamma di problemi di ottimizzazione.- Es: algoritmi genetici (risolvono problemi come lo zaino, il TSP, problemi di scheduling, problemi di ottimizzazione discreti, continui ecc...).
Tecnica: È uno schema per un possibile algoritmo (ci sono dei buchi da riempire che dipendono dal problema e altri possono essere scelti dal programmatore).- Molte metaeuristiche usano i numeri casuali (pseudo casuali). Significa che sono algoritmi randomizzati.
- Più esecuzioni possono tornare soluzioni diverse:
- si prende la migliore oppure la media delle soluzioni
- Più esecuzioni possono tornare soluzioni diverse:
- Si utilizza in problemi di ottimizzazione discreta.
Le soluzioni nello spazio di ricerca sono connesse e formano un grafo orientato.
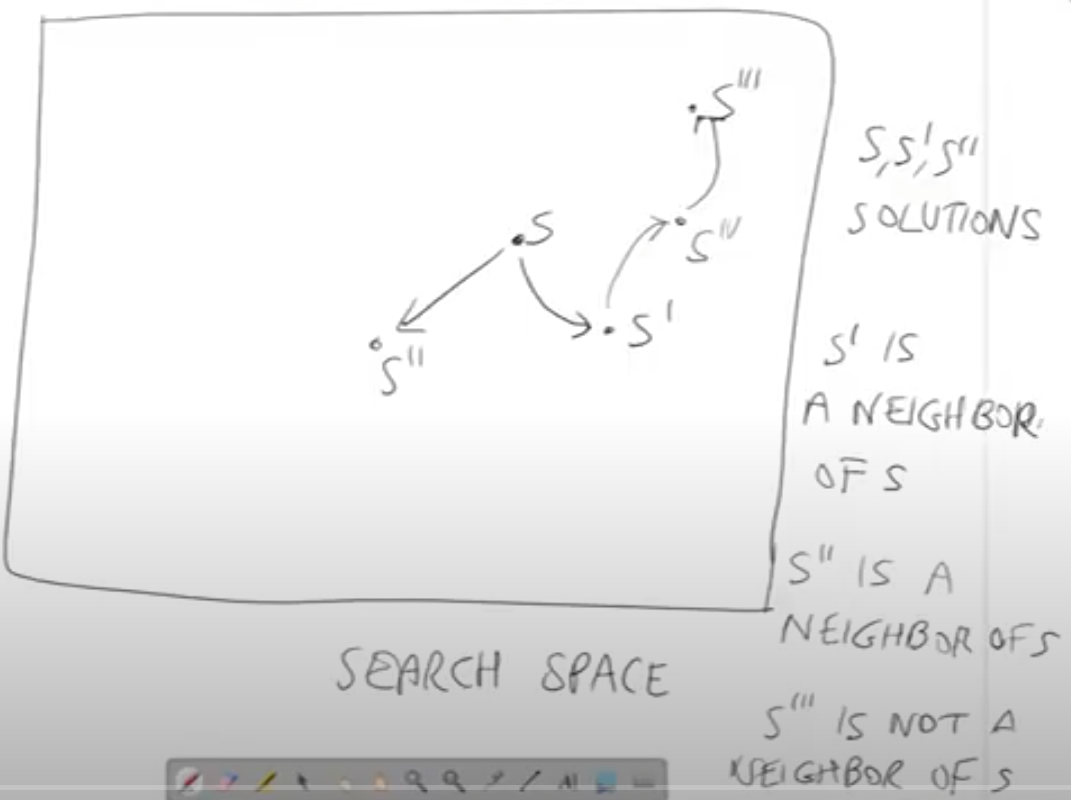
- S, S' e S'' sono soluzioni
- Si dice che S' è un vicino di S
- S'' è un vicino di S
- S''' non è vicino di S
S' è un vicino di S se:
- C'è un arco che va da S a S'
- S' può essere ottenuto da S usando una trasformazione elementare.
Primo esempio:
- dati n numeri interi
$x_1$ , ... ,$x_n$
Dividere i numeri in due sottoinsiemi disgiunti$S_1$ e$S_2$
Per esempio:
Una soluzione di NPP è una coppia di sottoinsiemi S1 e S2.
Ma una differente rappresentazione può essere basata su un vettore di n-bit b.
{14, 20, 8, 10} {13, 21, 9, 4} -> [00101011]
- La rappresentazione binaria è chiamata genotipo ed è una rappresentazione interna (può essere ad esempio utilizzata da un algoritmo in modo efficace)
- La rappresentazione sui sottoinsieme è chiamata fenotipo ed è una rappresentazione esterna.
La differenza sta che l'utente è interessato al fenotipo e invece l'algoritmo può utilizzare il genotipo perchè potrebbe funzionare meglio.
Il passaggio(mapping) da genotipo a fenotipo e viceversa deve essere computazionalmente veloce e facile, ma potrebbe non essere necessariamente 1:1 (ad un genotipo corrisponde ad un fenotipo, l'importante è che ogni genotipo abbia un fenotipo diverso. Potrebbero esserci due genotipi che corrispondono ad un fenotipo).
Un algoritmo può decidere di usare una rappresentazione ridondante dove differenti genotipi corrispondono allo stesso fenotipo.
Ritornando all'esempio di prima:
Fenotipo
Genotipo b
Tra i vettori di n-bit c'è l'operazione elementare chiamata bit-flip.
Dato un vettore n-bit e un indice i<= k <= n, negare il k-esimo bit
b = [00101100]
k = 5
b -> [00100100]
[00101100] si può trasformare in tanti modi applicando il bit-flip a tutti i possibili bit. Esempi:
- [10101100]
- [01101100]
- [00001100]
I possibili vicini di questa soluzione sono 8 e ognuno si ottiene facendo il flip di un bit.
Lo spazio di ricerca del NPP con la rappresentazione binaria è composto da
Questo spazio di ricerca si chiama ipercubo:
- per n=2 è un quadrato
- per n=3 è un cubo
- n = 4 non è facilmente disegnabile
- ecc...
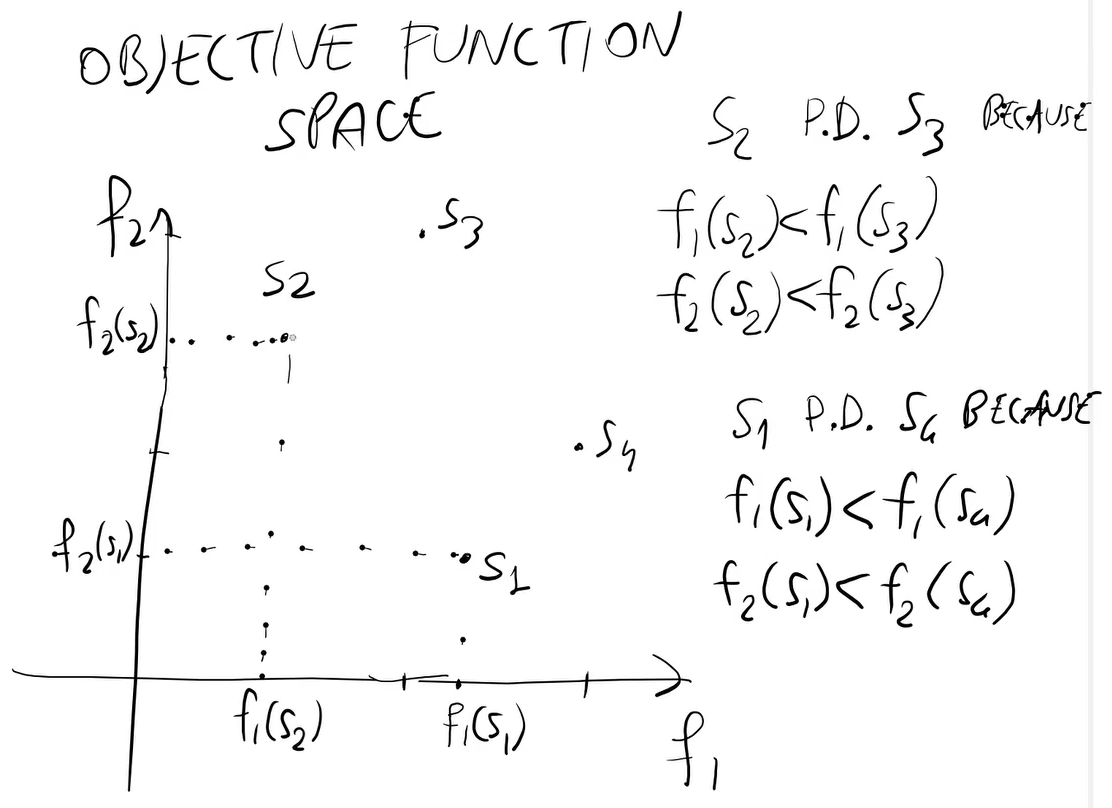
La funzione obiettivo
Partendo da una soluzione b, alcuni vicini (b') potrebbero essere migliori e altri (b'') potrebbero essere peggiori. Altri vicini possono essere buoni quanto b. Il paragone dei vicini si fa considerando le funzioni obiettivo.

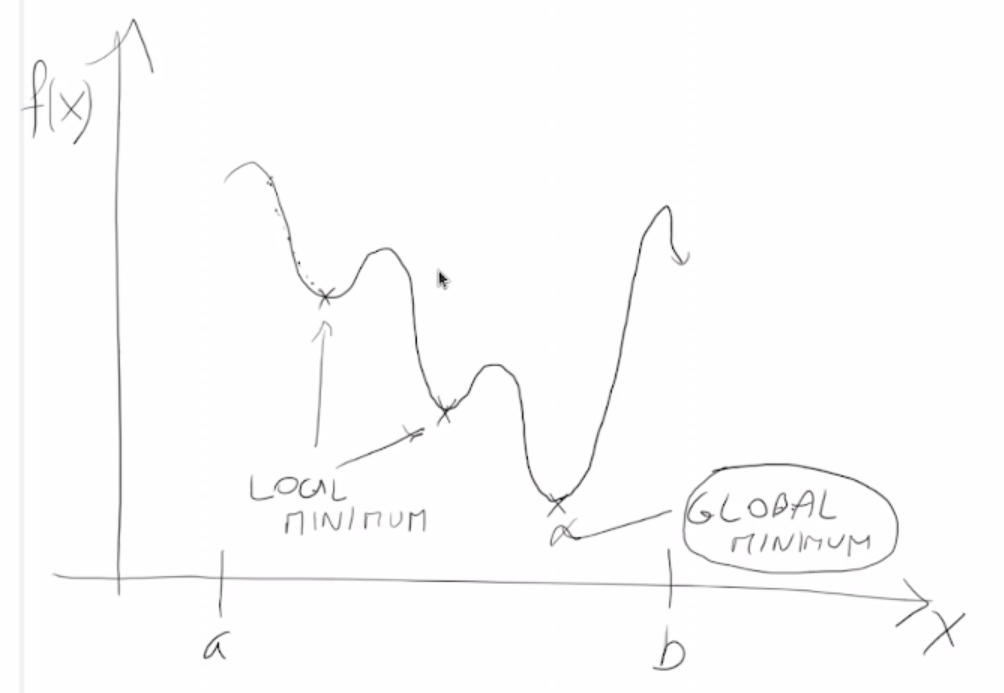
In NPP è il minimo locale.
- L'ottimo locale è una soluzione x | nessun vicino è meglio di x, ∀ y | y è vicino di x , f(y) >= f(x).
- x è un minimo locale stretto se ∀ y | y è vicino di x, f(y) < f(x).
NOTAZIONE: N(x) = {vicini di x}
Minimo:
- locale -> confronto con i vicini.
- globale -> confronto il punto con tutti
- Un minimo globale per una funzione f è una soluzione x | f(x) <= f(y) ∀ y ∈ X
- Un minimo globale stretto f(x) < f(y) ∀ y ∈ X
Il problema di ottimizzazione è risolto se trovo il minimo globale. Altrimenti ho trovato una soluzone sub-ottimale.
Un semplice algoritmo che trova un minimo locale si chiama Local Search.
function_LS(f,X)
x: scelto randomicamente (o con qualhe criterio) (soluzione)
found = false
do
y:= migliore dei vicini di x (prendo x trovo i vicini, calcolo f e prendo quella con valore più basso)
if f(y) >= f(x) then
found:= True
else
x:= y
while not found
return x
Come scegliere il miglior vicino?
y:= primo elemento di N(X)
fy:= f(y)
for z in N(X)
fz:= f(z)
if fz < fy then
y:= z
fy:= fz
end if
end for
return y
- È facile provare che LS restituisce sempre il minimo locale. C'è qualche probabilità di ottenere il minimo globale anche se solitamente la soluzione restituita ottenuta non è il minimo globale.
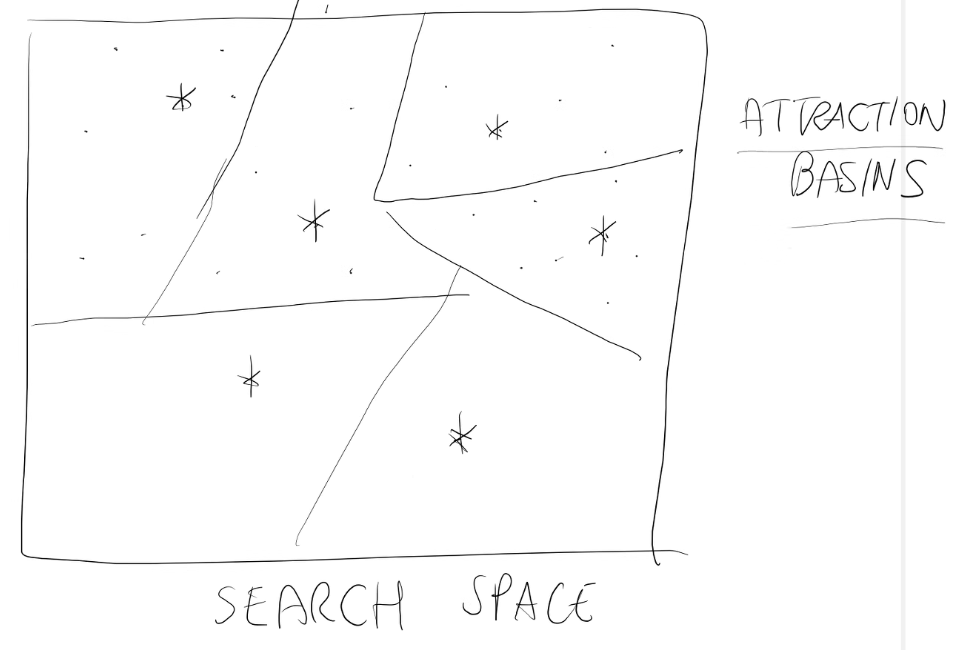
L'attrazione del bacino su un minimo local x* è l'insieme delle soluzioni x tali che se LS parte da x produce x*.
- L'algoritmo di ricerca locale appena visto è chiamato best improvement local search.
Un'altra possibilità è di scegliere (se c'è) un vicino di x che è migliore di x (non il migliore) -> first improvement local search
Function_LS_fi(X,f)
x:= initial solution (Random)
fx:= f(x)
found = false
do
y, fy := un vicino migliore di x (esplora N(X) con un ordine casuale)
if y = Φ (vuoto) then
found:= true
else
x:= y
fx:= fy
while not found
return x
Elementi dell'algoritmo:
- LS con scelta iniziale della soluzione
- nt = numero di tentativi del secondo tipo (tentativi infruttuosi)
Function_ILS(f,X, nt)
x0:= sluzione iniziale
x, fx := LS(f, X, x0)
k = 0
while k <= nt
y:= perturbation(x)
z, fz := LS(f,X, y)
if fz < fx then
x:= z
fx:= fz
k:= 0
else
k:= k+1
end if
end while
return x
- La perturbazione è una piccola modifica.
- Deve essere piccola perchè se lo stravolgo mi sposto troppo ed è come se ricominciassi da zero.
- h rappresenta la forza della perturbazione
- Per esempio in NPP h è il numero dei bit-flip applicati a x.
I concetti di local minimum e global minimum e gli algoritmi LS e ILS funzionano per ogni problema di ottimizzazione discreta data la struttura di vicinato.
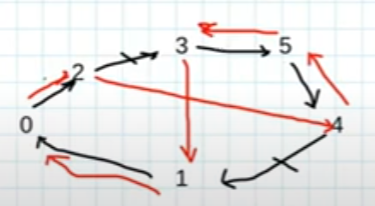
Per esempio nel TSP i vicinati
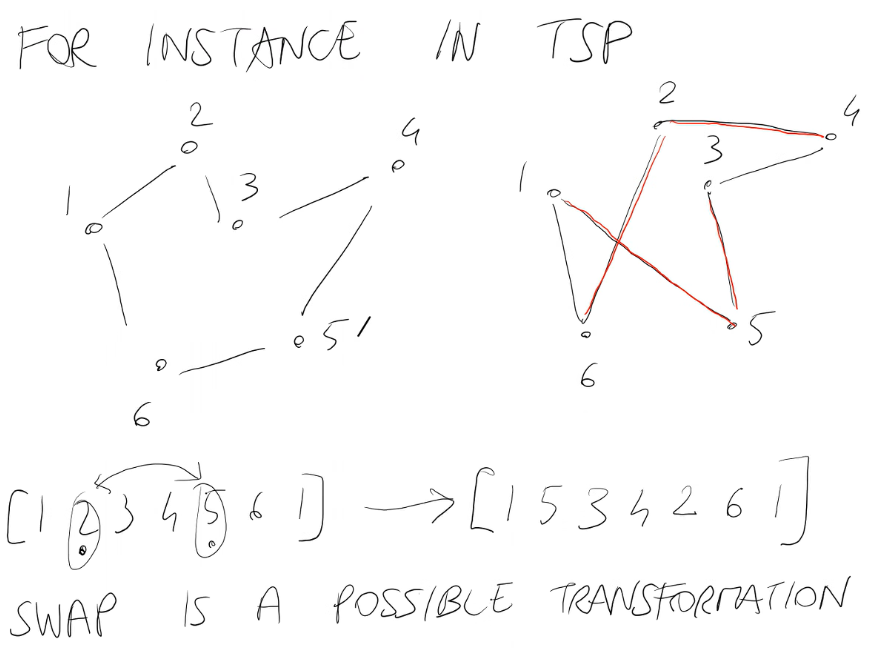
in rosso gli archi che non c'erano.
Innanzitutto è necessario definire la classe Problem per definire la struttura di base del problema, la sua inizializzazione e le funzioni di comodo.
# number partition problem
import numpy as np
class Problem:
def __init__(self, num):
self.dim = num
self.numbers = np.random.randint(1, 100000, num) # Creazione istanza
def objective_function(self, sol):
# La soluzione è un vettore di 0 e di 1
'''
- 0 rappresenta che stanno nel primo sottoinsieme
- 1 rappresenta che stanno nel secondo sottoinsieme
'''
s = 0
for i in range(self.dim):
if sol[i] == 0:
s += self.numbers[i]
else:
s -= self.numbers[i]
return abs(s)
def objective_function(self, sol): # Molto più efficiente
s = sum((1-2*sol)*self.number)
return np.abs(s)
def get_dim(self):
return self.dimSi può ora procedere all'implementazione dell'algoritmo di ricerca Local Search
import numpy as np
from NPP import *
# local search algorithm for a binary problem
# BEST IMPROVEMENT
def local_search(prob, init_sol=None):
n = prob.get_dim()
if init_sol is None:
x = np.random.randint(0, 1+1, n)
else:
x = init_sol.copy()
improved = True
fx = prob.objective_function(x)
print("Initial value {}".format(fx))
while improved:
best_f = 1e300 # Numero grande per i confronti seguenti
for i in range(0, n):
x[i] = 1-x[i] # Bit-flip -> questa logica può essere migliorata e resa più efficiente in quanto ci mette O(n^2) operazioni
fy = prob.objective_function(x)
if fy < best_f:
y = x.copy()
best_f = fy
x[i] = 1-x[i]
if best_f < fx:
fx = best_f
x = y
improved = True
print("New value {}".format(fx))
else:
improved = False
return x, fx - Il bit-flip può essere chiamato Δf(x, i) = f(x con i-esimo bit complementare) - f(x)
Nel problema NPP è anche semplice trovare il miglior vicino di x, in O(n) anzichè$O(n^2)$ .
A sua volta se riduco il tempo di ricerca della Local Search lo riduco anche delle versione iterata in quanto usa essa stessa.
Per testare l'algoritmo e vedere le varie info si consigliano i seguenti comandi (disponibili nel file test.py nella directory apposita).
from local_search import *
np.random.seed(42) # Fisso il seed per la riproducibilità degli esperimenti
p = Problem(100) # Creo istanza problema di lunghezza 100
print(p.numbers) # Stampo i vari numeri che popolano il vettore popolato randomicamente
print(p.get_dim())
x, fx = local_search(p) # Eseguo la Local Search
print(x, fx)
x, fx = local_search(p,x) # Se la rieseguo partendo dalla soluzione di prima si vede che ritorna sempre lo stesso valore e quindi non migliora
risultati = [local_search(p) for run in range(100)] # Eseguo Local Search 100 volte
print(risultati)
# Analisi sui valori dei risultati ottenuti
ff = [coppia[1] for coppia in risultati]
min = np.min(ff)
# Altri tipi di analisi
'''
np.mean(ff)
np.max(ff)
np.min(ff)
np.median(ff)
'''Si passa ora all'implementazione della Local Search nella sua versione First improvement.
import numpy as np
from NPP import *
# local search algorithm for a binary problem
# FIRST IMPROVEMENT
def local_search(prob, init_sol=None, verbose= False):
n = prob.get_dim()
if init_sol is None:
x = np.random.randint(0, 1+1, n)
else:
x = init_sol.copy()
improved = True
fx = prob.objective_function(x)
if verbose:
print('Initial value {}'.format(fx))
while improved:
best_f = fx
ordering = list(range(0,n))
np.random.shuffle(ordering)
for i in ordering:
x[i] = 1-x[i]
fy = prob.objective_function(x)
if fy < best_f:
y = x.copy()
best_f = fy
x[i] = 1-x[i]
break
x[i] = 1-x[i]
if best_f < fx:
fx = best_f
x = y
improved = True
if verbose:
print("New value {}".format(fx))
else:
improved = False
return x, fx Questa versione è molto più veloce di quella precedente.
from local_search_fi import *
from NPP import *
def iterated_local_search(prob, num_tries, num_flips, init_sol= None):
n = prob.get_dim()
if init_sol is None:
x = np.random.randint(0, 1+1, n)
else:
x = init_sol.copy()
nt = 0
fx = prob.objective_function(x)
while nt < num_tries:
y =perturbation(x, num_flips)
z, fz = local_search(prob, y)
if fz < fx:
x = z
fx = fz
nt = 0
else:
nt+=1
return x, fx
def perturbation(x, num_flips):
n = len(x)
y = x.copy()
for flip in range(num_flips):
i = np.random.randint(0, n)
y[i] = 1 - y[i]
return yQuest'ultima può essere in realtà implementata utilizzando entrambe le tipologie di Local Search (best improvemente e first improvement), con la quale si noteranno differenti prestazioni in termini di tempo e probabilmente anche della soluzione trovata.
Per quanto riguarda il codice sorgente completo, eventuali comandi di test e altro vedere i relativi file nell'apposita directory per la Local Search.
- Nella ricerca locale (anche nella sua versione iterata), si passa da un elemento x a un elemento migliore.
- Nella ricerca locale il passaggio avviene in maniera diretta perchè si prende un vicino di x e lo si cerca di migliorare passando per uno dei vicini di quest'ultimo.
- Nella ricerca locale devo quindi migliorare ad ogni passaggio. Quando non è più possibile, l'algoritmo termina.
- Nella ricerca locale iterata, il procedimento è diverso, ma ad ogni passaggio si deve comunque migliorare.
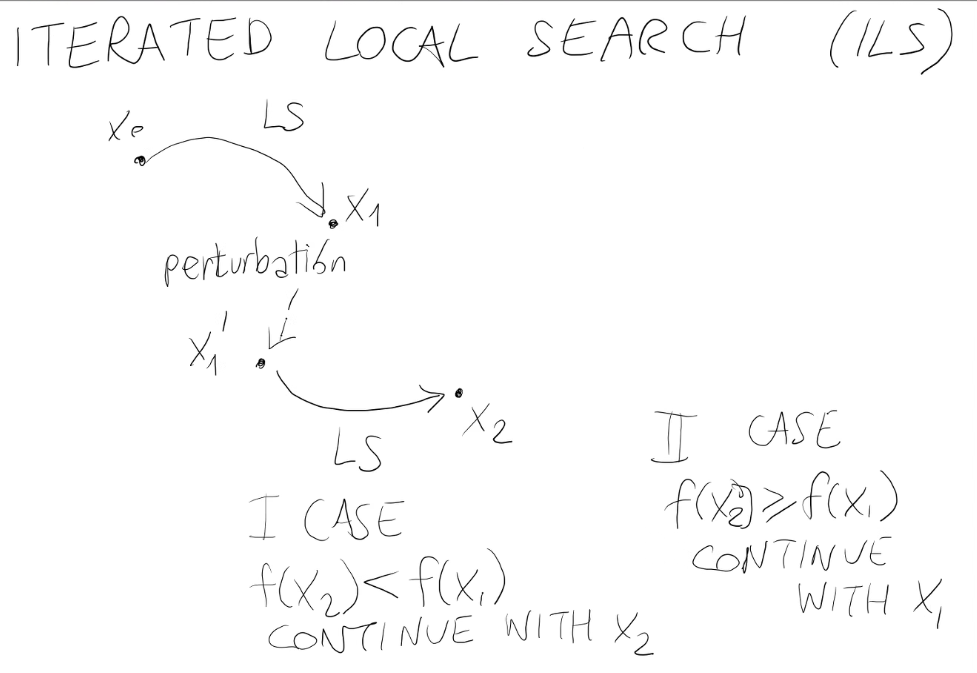
Si parte da un punto x0, si applica la ricerca locale e si arriva in x1 (minimo locale). Si applica una perturbazione a quest'ultimo (che potrebbe anche peggiorare la situazione ma non importa) e si riapplica la ricerca locale arrivando in z. Se z è migliore la ricerca procede da questo punto, se invece ho peggiorato non si accetta (perchè si deve comunque sempre migliorare).
Dopo un tot di tentavi infruttuosi la ricerca termina (oppure si possono scegliere altre condizioni di terminazione. Es. quante volte ho valutato f).
Nel Simulated annealing invece, si può anche peggiorare (ma di poco) e soprattutto all'inizio.
Si intende che le soluzioni possono anche peggiorare.
x:= initial solution # può essere preso random
fx:= f(x)
t:= initial temperature
for i:= 1 to num_iterations
y:= selecet a random neighbor of x
fy:= f(y)
df=fy-fx # differenza in f
p:= exp(-df/t) # se df è negativo, p è maggiore di 1
if random(0,1) < p then # Se fy<fx, y è accettato come nuovo valore di x
x:= y
fx:= fy
end if
t:= t * delta_t # delta_t = 0.95
end for
return x, fx
Cosa accade?
Quando f(y) >= f(X), y è accettato con una probabilità exp(-df/t).
Più è basso df e maggiore è la probabilità di accettazione. Se la differenza fosse 0 o negativa, lo accetterebbe sempre.
Maggiore è t, maggiore è la probabilità di accettazione.
- I peggioramenti non gravi sono quindi accettati meglio dei peggioramenti gravi.
- I peggioramenti sono accettati soprattutto quando la temperatura è alta.
È altresì importante che la temperatura diminuisce mano a mano.
All'inizio quindi la tendenza ad accettare peggioramenti è alta e poi scende. Verso la fine il simulated annealing (SA) accetta solo miglioramenti (perchè la probabilità di accettazione è così bassa che è come se fosse 0).
Questo algoritmo è molto più casuale (randomico) della ricerca locale e della ricerca locale iterata (vedere quanti eventi random ci sono nello pseudocodice).
- È molto più randomico di LS e ILS
- C'è un bilanciamento tra exploration e exploitation.
Exploration: guardare intorno a x (esplorare lo spazio di ricerca), senza prendere troppo in considerazione la funzione obiettivo f.
Exploitation: cerca necessariamente il vicino migliore.
All'inizio prevale l'exploration e mano a mano che la temperatura scende, la componente di exploitation prevale. - SA può essere usato anche per l'ottimizzazione continua, facendo una piccola modifica (Vedi sotto).
Ottimizzazione continua: x non è un vettore o una permutazione di numeri (0 e 1), ma è fatto di numeri reali (il concetto di vicini non ha senso nei numeri reali).
y:= x+delta_x
dove delta_x è un vettore di numeri casuali piccoli nell'intervallo [-epsilon, +epsilon].
Ciò indica "muoviti da x di un passettino".
Uno dei problemi principali di SA è come gestire la temperatura:
- trovare il valore iniziale per t_init
- trovare come aggiornare t
L'implementazione seguente tratta l'algorimto SA sul problema NPP, quindi è necessario fare riferimento al file NPP.py.
import numpy as np
from NPP import *
# simulated annealing per il problema binario
def simulated_annealing(prob, num_iter, init_sol=None):
n = prob.get_dim()
if init_sol is None:
x = np.random.randint(0, 1+1, n)
else:
x = init_sol.copy()
fx = prob.objective_function(x)
temp = 0.1 * fx / (-np.log(0.5))
for i in range(num_iter):
j = np.random.randint(0, n)
y = x.copy()
y[j] = 1 - y[j]
fy = prob.objective_function(y)
df = fy - fx
pr = np.exp(-df / temp)
if np.random.random() < pr: # if fy < fx or np.random.random() < pr
x = y
fx = fy
temp = temp*0.95
return x, fxIl codice per fare eventuali test è il seguente:
from NPP import *
from simulated_annealing import *
np.random.seed(1918)
instance = Problem(100)
x, fx = simulated_annealing(instance, 10000)
print(x, fx)Nel caso in cui si abbia overflow nel decadimento di temp cambiare il tasso di decadimento (qui è 0.95).
TSP = problema del commesso viaggiatore.
In questo problema, una soluzione è una lista di vertici tale che:
- inizia e finisce con lo stesso vertice
- non ha vertici duplicati (tranne il primo e l'ultimo)
- ha lunghezza n+1
Nel TSP ci sono vari concetti di vicini (possibili implementazioni):
-
SWAPE/EXCHANGE
x =[0 2 3 5 4 1 0]---> x' (vicino) =[0 2 1 5 4 3 0]
Ci sono O(n^2) vicini. -
2-OPT
Tecnica 2-OPT : prendo due archi che non devono essere vicini e li inverto.
x =[0 2 3 5 4 1 0]---> x' (vicino) =[0 2 4 5 3 1 0]
Ci sono sempre$O(n^2)$ vicini
2-OPT ha un'interessante proprietà:
File per il TSP
import numpy as np
class Problem_tsp:
def __init__(self, nc, mat):
self.ncities = nc
self.dmat = mat # Matrice che contiene le distanze
def create_random_instance(nc):
# Crea due vettori x e y che contengono le coordinate di ciascuna città nel range [-50,50]
x = 100 * np.random.random(nc) - 50
y = 100 * np.random.random(nc) - 50
m = np.zeros((nc, nc))
for i in range(nc):
for j in range(nc):
m[i,j] = np.sqrt((x[i]-x[j])**2+(y[i]-y[j])**2)
return Problem_tsp(nc,m)
# l è l'elenco dei nodi visitati, includendo il primo e l'ultimo (che sono uguali)
def objective_function(self, l):
s = 0
for i in range(self.ncities):
c1 = l[i]
c2 = l[i+1]
d = self.dmat[c1,c2]
s = s+d
return s
def do_2_opt(l, i, j):
l1 = l[:i+1]
l2 = l[i+1:j]
l3 = l[j:]
return l1+l2[::-1]+l3
# Compute the difference on the objective functuion if the 2-opt operation is performed
def delta_2_opt(self, l, i, j):
return -self.dmat[l[i], l[i+1]] - self.dmat[l[j-1], l[j]] + self.dmat[l[i], l[j-1]] + self.dmat[l[i+1], l[j]]Il delta è in grado di calcolare quanto cambia la funzione obiettivo se io applico il 2-opt, senza però farlo effettivamente e senza ricalcolare interamente la funzione obiettivo.
Effettuare 2-opt e ricalcolare la funzione obiettivo costa O(n), invece così costa O(1).
A questo punto si può implementare una ricerca locale che usa 2-opt.
def local_search(self, init_sol=None, verbose=False):
n = self.ncities
if init_sol is None:
# Creazione di una soluzione casuale
x = list(range(1, n))
np.random.shuffle(x)
x = [0]+x+[0]
else:
x = init_sol.copy()
improved = True
fx = self.objective_function(x)
if verbose:
print("Initial value {}".format(fx))
while improved:
best_delta = 1e300 # Numero grande per i confronti seguenti
# Il delta sarebbe quanto aumenta la funzione obiettivo se io faccio la 2-opt (l'obiettivo è averlo più basso possibile)
for i in range(1, n-1): # Controllo cosa succede se applico 2-opt senza effettivamente modificare x (lo cambio solo dopo aver trovato la migliore configurazione possibile)
for j in range(i+3, n):
delta = self.delta_2_opt(x, i, j)
if delta < best_delta:
i_best = i
j_best = j
best_delta = delta
if best_delta < 0:
fx = fx + best_delta
x = Problem_tsp.do_2_opt(x, i_best, j_best)
improved = True
if verbose:
print("New value {}".format(fx))
else:
improved = False
return x, fx Per provare l'implementazione, vedere il file test2.py. Qui di seguito sono comunque riportati dei comandi di esempio.
from TSP import *
p = Problem_tsp.create_random_instance(50)
print(p.ncities)
print(p.dmat)
l = list(range(0, 50))
l.append(0)
print(len(l))
print(p.objective_function(l))
l1 = Problem_tsp.do_2_opt(l, 22, 44)
print(p.objective_function(l1))
delta = p.delta_2_opt(l, 22, 44)
print(delta)
print(p.objective_function(l)+delta)
p = Problem_tsp.create_random_instance(20)
print(p.local_search(verbose=True))- applicare ILS
- applicare SA
Per quanto riguarda le istanze del TSP, è possibile:
- generarle a caso
- leggerle da file
- Sono disponibili delle repo contenenti varie istanze
Vedi:
- Sono disponibili delle repo contenenti varie istanze
Gli Algoritmi evolutivi si dividono in 3 sottoclassi principali:
- Algoritmi Genetici (GA)
- Strategie Evolutive (ES)
- Programmazione Evolutiva (EP)
Tra questi, i GA si sono rivelati i più popolari dei 3. Questi algoritmi sono simili in generale, ma ci sono grandi differenze tra loro.
Somiglianze e differenze:
- Tutti e 3 operano su stringhe di lunghezza fissa, che contengono valori reali in ES e EP e numeri binari nel GA canonico.
- Tutti e 3 incorporano un operatore di mutazione: per ES e EP la mutazione è la forza trainante. GA e ES utilizzano anche un operatore di ricombinazione, che è l'operatore principale per GA (crossover).
- Tutti e 3 utilizzano un operatore di selezione che applica una pressione evolutiva, istintiva (in ES e EP, l'operatore determina quali individui saranno esclusi dalla nuova popolazione) o conservante (in GA l'operatore seleziona gli individui per la riproduzione).
- In GA e EP la selezione è probabilistica, mentre gli ES utilizzano una selezione deterministica. ES e meta-EP consentono l'autoadattamento, in cui i parametri che controllano la mutazione possono evolversi insieme alle variabili oggetto. Infine, vale la pena notare che l'implementatore è libero di modificare questi algoritmi.
È l'algoritmo più famoso in letteratura.
L'algoritmo genetico si applica per risolvere un problema di ottimizzazione.
È la più famosa metaeuristica.
È basata su una metafora semplice da capire
- L'algoritmo usa una popolazione di individui
- Ciascun individuo è una soluzione del problema ed è rappresentato in genere come una stringa (binaria)
Questa popolazione è modificata attraverso 3 operazioni
- Crossover
- Mutazione
- Rimpiazzamento
C'è anche un'operazione antecedente al crossover:
0. selezione: non modifica la popolazione, serve come punto di partenza per il crossover
La rappresentazione degli individui è detta cromosomi.
- Ogni individuo è rappresentato come un cromosoma. Il cromosoma è il patrimonio genetico di un individuo.
Altre caratteristiche:
- Gli GA (genetich algorithm) sono molto studiati in molti articoli scientifici. Sia dal punto di vista teorico che dal punto di vista applicativo.
- GA possono essere applicati a moltissimi problemi di ottimizzazione, sia discreti che continui.
- GAs hanno una predisposizione per il discreto. Sono naturalmente applicati a problemi discreti perchè gli individui sono stringhe.
- GA sono stati introdotti da Holland nel 1970 e da allora sono la metaeuristica più famosa in assoluto (da allora sono studiati e applicati in tantissime situazioni in cui gli algoritmi tradizionali non riescono a funzionare).
s = [0,1,0,1,0,0,1,1]
- 8 alleli, ciascuno dei quali contiene un 0 o 1 (che sono chiamati geni)
- gli alleli sono le posizioni
- i geni sono che cosa contiene
Ripassando, nei GA si ha:
- f funzione obiettivo
- X spazio di ricerca
- Popolazione di N individui, chiamati cromosomi.
- Ciascun cromosoma codifica una soluzione, cioè un elemento di X
Se il cromosoma c è direttamente la soluzione, f può essere applicata al cromosoma c.
Altrimenti f deve essere riscritta (ridefinita) in modo da poter essere applicata a c, oppure c deve essere decodificato in modo da ottenere la soluzione corrispondente.
Esempio:
Sono possibili molte rappresentazioni dello spazio di ricerca X:
- Un cromosoma è la lista dei vertici visitati
[0, 2, 3, 1, 5, 4, 0] - Un cromosoma è la lista degli archi visitati
[(0,2), (2,3), (3,1), (1,5), (5,4), (4,0)] - Un cromosoma è una matrice binaria di dimensione n x m tale che l'elemento M[i,j] = 1 se e solo se l'arco (i-->j) è visitato.
Questa rappresentazione funziona correttamente solo se il TSP è simmetrico. - Potrebbero esistere anche altre rappresentazioni
La funzione obiettivo f va quindi riscritta per ognuna di queste rappresentazioni, oppure decido una volta per tutte quale deve essere la rappresentazione esterna, scrivo la funzione per quest'ultima e ogni volta che l'algoritmo genetico deve valutare f trasformo il cromosoma in soluzione.
Quindi, ci sono 2 approcci per valutare la funzione obiettivo:
- Scrivo il codice per valutare f secondo la rappresentazione.
- Scrivo un codice per valutare f usando uno standard per la soluzione (per esempio una lista di vertici visitati).
Ogni volta che la funzione deve essere valutata da GA, si traduce il cromosoma nella forma standard applicando una funzione di decodifica per ottenere la soluzione.
Quindi, GA può decidere, per qualsiasi motivo, una rappresentazione interna (GENOTIPO) diversa da quella su cui l'utente ragiona (rappresentazione standard) (FENOTIPO).
function GA(X, f, //parametri del problemma
N, Ngen, pCross, pMut) //parametri dell'algoritmo
inizializzo la popolazione
for g:=1 to Ngen
select the mating pool
apply the crossover operation
apply the mutation operator
update the population
end for
return il miglior individuo trovato x* e il corrispondente f value f(x*)
Cosa significa il miglior individuo trovato?
- Molte metauristiche possono produrre, in qualsiasi passaggio, individui che sono peggiori o migliori di quelli prodotti nei passaggi precedenti.
- Quindi ha senso memorizzare il miglior individuo trovato fino a quel punto (stato corrente).
- C'è quindi una variabile nell'algoritmo che mi permette di controllare se il nuovo individuo è migliore di quello momentaneamente memorizzato.
- Li confronto e in caso positivo salvo quello nuovo.
Ciò è molto utile se:
- L'algoritmo non sempre accetta miglioramenti
- L'algoritmo usa qualche meccaniscmo di restart (non riesco a migliorare allora provo a ripartire)
NOTA: Miglior individuo trovato -> variabile che conserva il miglior individuo di sempre.
La popolazione può essere inizializzata in 3 modi principali:
- Completamente a caso
- Se il problema non ha vincoli, tutte le soluzioni sono valide.
- Creare solo cromosomi validi
- Se il problema ha vincoli (ad esempio il problema dello zaino), significa che non tutti gli individui rappresetano una soluzione valida
- Creare 'buoni' individui (non così scarsi). Per esempio utilizzando un'euristica h che mi permette di farlo.
- se h è deterministica, può produrre un solo individuo. Di conseguenza gli altri N-1 vanno scelti a caso.
- in generale, usare h solo per generare soltanto alcuni individui e gli altri generati in modo casuale.
- euristica è dipendente dal problema
- la metaeuristica no
Tornando alla spiegazione dello pseudocodice dell'algoritmo:
Primo passaggio:
- select of the mating pool M
Definizione.
Il mating pool M è un insieme di N/2 coppie di individui presi dalla popolazione (per esempio la popolazione attuale).
- M è usato per il passaggio successivo (Crossover)
- L'idea principale è di scegliere i migliori individui
Come scegliere gli individui migliori?
- Roulette wheel
- Tornei
- Selezionare un individuo in modo casuale secondo la probabilità (in modo proporzionale) alla fitness F per ogni individuo.
- Un GA ha l'obiettivo implicito di massimizzare il valore di fitness degli elementi della popolazione degli individui.
- Posso accontentarmi anche di un singolo individuo con un alto valore di fitness F
- Un GA ha l'obiettivo implicito di massimizzare il valore di fitness degli elementi della popolazione degli individui.
Caratteristiche:
- Se il problema è di ottimizzazione è un problema di massimizzazione:
- F può coincidere con la funzione obiettivo f.
- Oppure F è una trasformazione crescente di f.
- Es. F(x) =
$f(x)^2$
- Es. F(x) =
- Se il problema di ottimizzazione è un problema di minimizzazione:
-
F deve essere una trasformazione decrescente.
- Es. F(x) = 1/f(x)
F(x) = 1000 - f(x)
F(x) = -log f(x)
- Es. F(x) = 1/f(x)
- In questo caso se
f(x1) < f(x2)(x1 è migliore di x1), alloraF(x1) > F(x2)(x1 ha un valore di fitness maggiore di x2) - Il TSP è un problema di minimizzazione
-
F deve essere una trasformazione decrescente.
Supponiamo che le fitness F(x) > 0 (siano tutte positive) per ogni x.
La probabilità di pescare l'individuo x[i] è data da:
F(x[i]) / F(x[1]) + F(x[2]) + ... + F(x[N])
Per esempio:
F(x1) = 10, F(x2) = 5, F(x3) = 15, F(x4) = 20, F(x5) = 10
p(x1) = 10 / (10 + 5 +15 +20 +10) ----> 10/60
p(x2) = 5/60
ecc....
- Per pescare un individuo, si genera un numero reale casuale r tra 0 e 60.
- Se r < 10 ---> estrai x1
- Se r è tra [10, 15[ ---> estrai x2
- se r è tra [15, 30[ ---> estrai x3
- se r è tra [30, 50[ ---> estrai x4
- se r è tra [50, 60[ ---> estrai x5
In questo modo genero ogni numero x[i] con una probabilità proporzionale a F(x[i]).
Il costo computazionale della singola estrazione è O(N).
- F può essere considerata anche come rank di x nella popolazione.
- F=N per il miglior individuo
- F=N-1 per il secondo miglior individuo
- ...
- F = 1 per il peggior individuo
- scelgo k individui a caso e scelgo il migliore tra di loro (a mo' di sfida)
-
è più veloce rispetto a fare la roulette wheel
- il costo di selezionare N/2 coppio è O(kN), invece di
$O(N^2)$ per la roulette wheel
- il costo di selezionare N/2 coppio è O(kN), invece di
In questo modo il peggior individuo non verrà mai selezionato (non ha chance di essere selezionato perchè prendendo anche solo due individui. Il peggiore non sarà mai scelto a meno che tra le selezioni degli individui io posso pescare più volte lo stesso individuo. In questo modo potrei prendere due peggiori e quindi viene selezionato).
Questi metodi di selezione possono produrre un mating pool con individui identici
- I migliori individui possono essere rappresentati più volte.
- Migliore è l'individuo e più coppie potrebbero esserci di lui.
- I peggiori individui potrebbere anche essere assenti nel mating pool.
- Se un individuo è molto più buono degli altri:
- con la roulette ci possono essere tante copie di lui a discapito degli altri
- con i tornei non è detta ma potrebbe esserci comunque un numero abbastanza alto di copie
- L'operazione di crossover prende due cromosoimi s1 e s2, genera 1 o 2 nuovi cromosomi
- s1 e s2 sono chiamati genitori
- I due nuovi cromosomi c1 e c2 sono chiamati figli
- Si parte quindi da N/2 coppie di individui
- p1, p2
- p3, p4
- ...
- p[N/2 -1], p[N/2]
Ciascuna di queste coppie è copiata e inviata allo step successivo (con probabilità 1-pCross) oppure è modificata utilizzando l'operatore di crossover (con probabilità pCross).
- Ciascuna coppia p[i], p[i+1] produce 2 figli c[i], c[i+1]
- c[i] = p[i] e c[i+1] = p[i+1] con probabilità 1-pCross
- c[i], c[i+1] = crossover(p[i] , p[i+1]) con probabilità pCross
Operazioni di Crossover:
Crea 2 figli (qualche volta un solo figlio ma deve essere applicato 2 volte, altre volte più figli e ne scelgo solo due) dai due genitori.
- one-point crossover:
- Utilizzato quando i due cromosomi sono stringhe o vettori di lunghezza fissa L
- seleziona un punto di taglio k casuale tra 1<=k<L
- Per esempio:
L'operazione chiamata
s1 = [0,1,0,1,0,0,1,1]
s2 = [1,1,0,1,0,1,0,0]
Si prende un punto di taglio e si crea un figlio con gli elementi a sinistra del taglio di uno e a destra del taglio dell'altro, e viceversa per l'altro figlio.
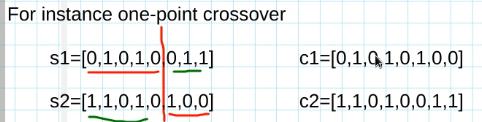
In questo modo si può vedere che ciascun figlio eredita parte del patrimonio genetico dal primo genitore e parte dal secondo.
Si può dire che il crossover mescola i patrimoni genetici di due elementi di una popolazione, creando due elementi che sono nuovi.
- È semplice gneralizzare il one-point crossover al multi-point crossover
- Crossover uniforme:
- i figli ereditano da un genitore o dall'altro in modo casuale
- Per esempio:

- Ci sono anche molti altri tipi di crossover per altri tipi di cromosomi
- Per esempio:
In TSP il one-point crossover non funziona bene- da una coppia di cromosomi validi(genitori), può produrre 2 figli non validi
p1 = 0 1 3 4 5 2 0p2 = 0 2 1 5 3 4 0- Se faccio il crossover ad un punto:

c1 visita 3 due volte, ma non visita 2.
c2 fa il contrario.
Il problema sta in questo punto. Questo perchè in una soluzione del TSP ogni figlio deve visitare ogni nodo esattamente una volta. - Questo metodo di ricombinazioni non è adatto per il TSP (e anche per altri problemi basati sulle permutazini).
- Neanche il Crossover uniforme funziona, ha ancora più chance di creare doppioni rispetto al one-point.
- Nel TSP si utilizzano altri sistemi per il crossover
- da una coppia di cromosomi validi(genitori), può produrre 2 figli non validi
- Per esempio:
Definizione.
Mutazione significa alterare il cromosoma dei figli.
I figli possono essere sia copie dei genitori o prodotti dal crossover (non è importante).
- Crea un nuovo individuo mutando/alterando un figlio appena prodotto dal crossover.
- c -----> c'
- Lo si altera ad esempio cambiando uno o più geni.
- Queste operazioni si possono fare sulla rappresentazione e non sull'individuo (differenza tra fenotipo e genotipo)
- Il crossover usa il materiale genetico dalla popolazione
- Il crossover ricombina tra loro cose che già esistono, non si hanno componenti nuovi per produrre individui. L'originialità è dovuta al fatto che li combino in modo diverso.
- Invece la mutazione può produrre nuove componenti
Può essere usato quando i cromosomi sono vettori o stringhe.
Altera ogni gene con una probabilità pMut (probabilità di mutazione).
c[i] = 0 1 0 1 0 0 1 1 1 0 (stringa di bit binaria)
pMut = 0.1
- Significa che in media solo un gene (bit) su 10 viene alterato.
- Con probabilità 1/10 lo altero
- Con probabilità 9/10 lo lascio invariato.
c'[i] = 0 1 0 1 0 1 1 1 1 0
NOTA: pMut in generale si tiene bassa
Si hanno questi elementi tra cui scegliere:
- N genitori (elementi della popolazione corrente)
- N figli (prodotti da crossover+mutazione)
- Valutare tutti gli N figli
- La nuova popolazione è composta dagli N figli (sostituzione dei genitori con i figli). Questo è ciò che accade a lungo andare in natura. Potrebbe tuttavia verificarsi che non tutti i figli siano adatti a vivere in questo ambiente.
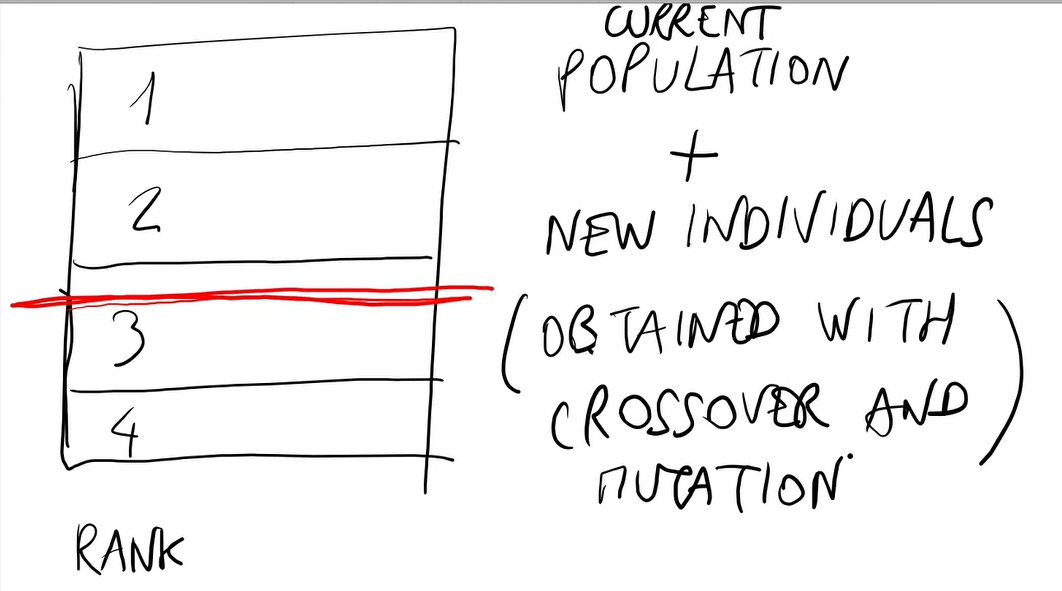
- Elitismo:
La nuova popolazione è composta da- K migliori individui tra i genitori e i figli
- N-K figli
Esempio:
K = 1 -> se il miglior individuo è un genitore, quest'ultimo viene selezionato e il peggior figlio non viene selezionato.
- Sopravvivono i migliori:
È una condizione particolare del punto precedente.
Ovvero K = N.
La nuova popolazione è composta dai N migliori individui tra i genitori e i figli.
Non importa quindi l'età. È possibile che il miglior individuo rimanga sempre nella popolazione (immortale). Ciò è possibile anche nell'elitismo.
L'implementazione di un algoritmo genetico richiede molte scelte:
- I parametri dell'algoritmo:
N-> grandezza della popolazionenum_gen-> numero di generazioni (iterazioni dell'algoritmo genetico)pCross-> probabilità del crossover (probabilità che una coppia selezionata durante il mating pool gli venga applicato il crossover)pMut-> probabilità della mutazione- Come si selezionano?
Si fanno un pò di tentativi. Non ci sono regole generali che funzionano sempre.
In generale- pCross dovrebbe essere abbastanza alto (tra 0.8 e 1)
- pMut dovrebbe essere bassa
- N dovrebbe andare di pari passo alla dimensione del problema. Un problema più grande dovrebbe avere una popolazione più grande
- Il numero di iterazioni (num_gen) dovrebbe essere sostituito da un altro criterio -> Criteri di terminazione
- Dopo num_gen iterazioni/generazioni (criterio di iterazioni)
- Dopo num_sec secondi (criterio temporale)
- Svantaggio: dipende dalla velocità di esecuzione del programma. Il criterio ha senso se voglio una risposta velocemente. Il criterio non ha senso se voglio testare algoritmi testati su macchine diverse, è dipendente dalla macchina.
- Termino quando la funzione obiettivo ha raggiunto un livello prefissato
- Criteri di terminazione
- Inizializzazione
- Selezione del mating pool
- Come fare il crossover
- Come fare la mutazione
- Come fare il rimpiazzamento (selezione della nuova popolazione)
Crossover e mutazione dipendono fortemente dal problema. Dipendono dalla rappresentazione che si fa delle soluzioni.
- Si deve implementare il problema (la classe, i suoi metodi e funzioni)
- Creare un'istanza a caso
- Caricare un'istanza da file
- Calcolare la funzione obiettivo (data una soluzione in qualche forma)
- Scegliere come rappresentare la soluzione (già qui si deve scegliere che rappresentazione utilizzare)
- Implementare il Crossover e la Mutazione per la rappresentazione scelta dal programmatore
- Il programamtore deve anche scegliere tutti i passaggi che devono essere fatti all'interno dell'algoritmo:
- Inizializzazione
- Criterio di terminazione
- Selezione
- Rimpiazzamento (replacement)
- (Eventualmente) Altri passaggi (non solo in GA ma anche in altre metaeuristiche):
- Metodi di ricerca locale per migliorare le soluzioni (combinare la forza di un GA con un algoritmo di ricerca locale: Algoritmo Memetico)
- Un possibile modo per applicare la ricerca locale è quello di cercare di migliorare la miglior soluzione trovata dal GA.
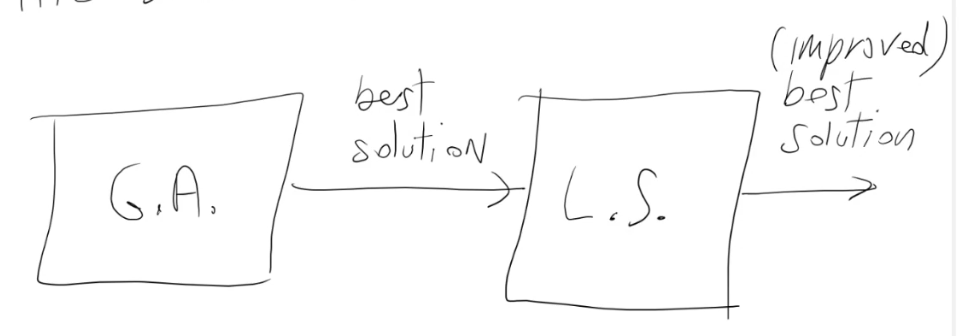
- Un altro possibile modo si applica nella situazione in cui talvolta la popolazione perde diversità (gli individui iniziano ad assomigliarsi molto l'un l'altro). La peggior situazione è che diventino tutti uguali.
Molti operatori di Crossover hanno la seguente proprietà:
Se p1 = p2 allora il Crossover(p1, p2) produce figli uguali ai genitori.
Quando un individuo è molto meglio degli altri (super-individuo), quest'ultimo tende a monopolizzare la popolazione (la porta ad essere simile a lui). Quando tutti gli individui sono uguali GA non funziona. L'unica operazione che potrebbe far uscire da questo stallo è la Mutazione.
Prima cosa: riconoscere quando la popolazione ha significativamente perso la sua diversità (ci sono varie tecniche per farlo).
Seconda cosa: Reagire (Ad esempio fermare l'algoritmo o reinizializzare la popolazione o una parte di essa, magari salvando la best solution ever found).
- Parametri
La configurazione di un algoritmo genetico (scegliere tutto quello che deve essere scelto, ovvero i parametri e i metodi) può essere automatizzata. Cioè io posso avere dei meccanismi che scelgono i parametri in maniera da ottimizzarli.
p1 = 0 2 3 5 1 6 4
p2 = 2 5 1 4 3 0 6
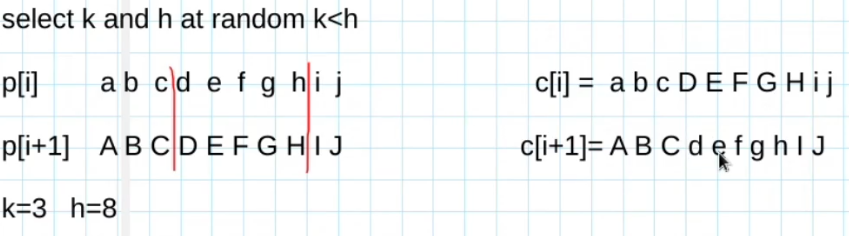
c1 prende gli elementi mancanti nell'ordine in cui si trovano in p2.
c1 = 2 4 3 5 1 0 6
c2 = 0 2 1 4 3 5 6
Questo si chiama ordered crossover:
- Significa prendere un segmento di ognuna delle due permutazioni, ricopiarlo nei figli e poi gli elementi che mancano, prenderli dall'altro genitore nell'ordine in cui si trovano (non nelle stesse posizioni).
Scambia k coppie in modo casuale.
K deve essere compatibile con pMut.
Esempio:
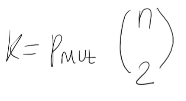
Dato un grafo non orientato G=(V,E) trovare un sottoinsieme
Un taglio è un arco (x,y) ∈ E tale che x ∈ U1, y ∈ U2 o x ∈ U2, y ∈ U1.
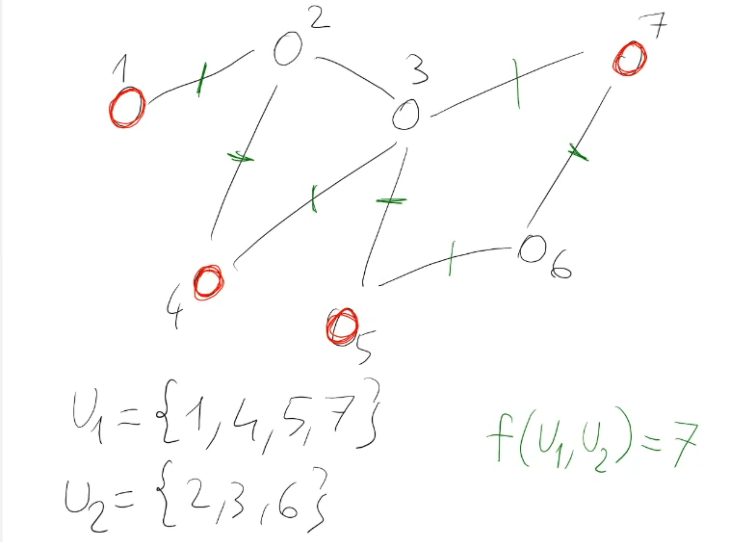
I tagli sono in verde. Un taglio è quindi un arco da un vertice di un insieme verso uno di un altro.
MAX-CUT è un problema NP-hard.
Lo scopo è quello di trovare
Una soluzione può essere descritta come una stringa di n-bit dove n è il numero dei vertici n=|V| (si presta bene agli algoritmi genetici).
# Un'istanza è data dal numero dei nodi numerati da 0 al numero di nodi -1 (0, . . ., num_nodes-1) -> se ho 6 nodi sono numerati da 0 a 5
# È data anche dalla lista degli archi (una coppia di nodi)
import numpy as np
class Maxcut_problem:
def __init__(self, num_nodes, edges):
self.num_nodes = num_nodes
self.edges = edges
def create_random_instance(num_nodes, edge_prob):
edges=[]
for i in range(0,num_nodes):
for j in range(i+1,num_nodes):
if np.random.random()<edge_prob:
edges.append((i,j))
return maxcut_problem(num_nodes,edges)
def objective_function(self,c):
# c è un vettore di n-bit
# c is a num_nodes binary string
num_cuts = 0
for x,y in self.edges:
if c[x]!=c[y]:
num_cuts +=1
return num_cuts
def get_dim(self):
return self.num_nodes# A simple genetic algorithm for unconstrained binary maximization problems
import numpy as np
class Binary_genetic_algorithm:
def __init__(self, problem, num_elem=None, num_gen=100, pcross=0.9, pmut=0.01):
self.problem=problem
self.num_bits=problem.get_dim()
if num_elem is None:
self.num_elem=self.num_bits
else:
self.num_elem=num_elem
self.pcross=pcross
self.pmut=pmut
self.num_gen=num_gen
def run(self):
self.init_population()
for gen in range(0,self.num_gen):
mating_pool=self.select_mating_pool()
children=self.do_crossover(mating_pool)
self.do_mutation(children)
self.select_new_population(children)
return self.best, self.best_f
def init_population(self):
self.population=[]
self.f_obj=np.zeros(self.num_elem)
self.best=None
self.best_f=-1
for i in range(0,self.num_elem):
ind=np.random.randint(0,1+1,self.num_bits)
self.population.append(ind)
self.f_obj[i]=self.problem.objective_function(ind)
self.update_best(ind,self.f_obj[i])
def update_best(self, x, fx):
if fx>self.best_f:
self.best_f=fx
self.best=x
print("new best ",fx)
def select_mating_pool(self):
mating_pool=[]
for i in range(0,self.num_elem//2):
p1=self.roulette_wheel()
p2=self.roulette_wheel()
mating_pool.append((p1,p2))
return mating_pool
def roulette_wheel(self):
s=np.sum(self.f_obj)
r=np.random.random()*s
i=0
while r>s:
r=r-self.f_obj[i]
i=i+1
return self.population[i]
def do_crossover(self, mating_pool):
children=[]
for p1, p2 in mating_pool:
if np.random.random()<self.pcross:
c1, c2 = self.crossover_operator(p1,p2)
else:
c1=p1.copy()
c2=p2.copy()
children.append(c1)
children.append(c2)
return children
def crossover_operator(self, p1, p2):
# one point crossover
l1=list(p1)
l2=list(p2)
j=np.random.randint(1,self.num_bits)
c1=np.array(l1[:j]+l2[j:])
c2=np.array(l2[:j]+l1[j:])
return c1,c2
def do_mutation(self,children):
for c in children:
for i in range(0, self.num_bits):
if np.random.random()<self.pmut:
c[i]=1-c[i]
def select_new_population(self,children):
# Find the best among the children and the parents
f_child=np.array([self.problem.objective_function(c) for c in children])
ib1=np.argmax(self.f_obj)
ib2=np.argmax(f_child)
# First case: the best child is better than the the best parent
if f_child[ib2]>self.f_obj[ib1]:
self.population=children
self.f_obj=f_child
self.update_best(children[ib2],f_child[ib2])
else:
iw=np.argmin(f_child)
children[iw]=self.population[ib1]
f_child[iw]=self.f_obj[ib1]
self.population=children
self.f_obj=f_child Per provare l'implementazione, vedere il file test.py. Qui di seguito sono comunque riportati dei comandi di esempio.
from binary_genetic_algorithm import *
from maxcut import *
p = Maxcut_problem.create_random_instance(20, 0.1)
g = Binary_genetic_algorithm(p, num_elem=20)
print(len(p.edges))
g.run()Qui di seguito è riportata l'implementazione del TSP, vedere l'apposito file nella directory degli algoritmi genetici.
class Tsp_problem:
def __init__(self,n_cities, dist_matrix):
self.n_cities=n_cities
self.dist_matrix=dist_matrix
def create_random_instance(n):
x=np.random.random(size=n)
y=np.random.random(size=n)
m=np.zeros((n,n))
for i in range(n):
for j in range(n):
m[i,j]=np.sqrt((x[i]-x[j])**2+(y[i]-y[j])**2)
return Tsp_problem(n,m)
def objective_function(self,x):
# x è la lista ordinata dei nodi visitati, eccetto l'ultimo vertice (che è anche il primo)
# 1 2 0 4 5 3 1
cost=0
for i in range(0,self.n_cities-1):
c1=x[i]
c2=x[i+1]
cost+=self.dist_matrix[c1,c2]
# Costo per tornare al primo
c1=x[-1]
c2=x[0]
cost+=self.dist_matrix[c1,c2]
return cost
def get_dim(self):
return self.n_citiesÈ ora necessario modificare l'algoritmo genetico definito per il problema del MAX-CUT in modo tale che sia possibile utilizzarlo per il problema TSP (vedi file permutation_genetic_algorithm.py).
# A simple genetic algorithm for unconstrained permutation minimization problems
import numpy as np
class Permutation_genetic_algorithm:
def __init__(self, problem, num_elem=None, num_gen=100, pcross=0.9, pmut=0.01):
self.problem=problem
self.num_nodes=problem.get_dim()
if num_elem is None:
self.num_elem=self.num_nodes
else:
self.num_elem=num_elem
self.pcross=pcross
self.pmut=pmut
self.num_gen=num_gen
def run(self):
self.improvements=[]
self.init_population()
for gen in range(1,self.num_gen+1):
mating_pool=self.select_mating_pool()
children=self.do_crossover(mating_pool)
self.do_mutation(children)
#self.select_new_population_best(children,gen)
self.select_new_population_elit(children,gen)
return self.best, self.best_f, self.improvements
def init_population(self):
self.population=[]
self.f_obj=np.zeros(self.num_elem)
self.best=None
self.best_f=1e300 # very large number
for i in range(0,self.num_elem):
ind=list(range(0,self.num_nodes))
np.random.shuffle(ind)
self.population.append(ind)
self.f_obj[i]=self.problem.objective_function(ind)
self.update_best(ind,self.f_obj[i],0)
def update_best(self, x, fx, g):
if fx<self.best_f:
self.best_f=fx
self.best=x
print("new best ",fx," at gen. ",g)
self.improvements.append((g,fx))
def select_mating_pool(self):
mating_pool=[]
self.fitness=np.array([1/f for f in self.f_obj])
for i in range(0,self.num_elem//2):
p1=self.roulette_wheel()
p2=self.roulette_wheel()
mating_pool.append((p1,p2))
return mating_pool
def roulette_wheel(self):
s=np.sum(self.fitness)
r=np.random.random()*s
i=0
while r>s:
r=r-self.fitness[i]
i=i+1
return self.population[i]
def do_crossover(self, mating_pool):
children=[]
for p1, p2 in mating_pool:
if np.random.random()<self.pcross:
c1, c2 = self.crossover_operator(p1,p2)
else:
c1=p1.copy()
c2=p2.copy()
children.append(c1)
children.append(c2)
return children
def crossover_operator(self, p1, p2):
ok=False
while not ok:
i1=np.random.randint(1,self.num_nodes-1)
i2=np.random.randint(1,self.num_nodes-1)
if i1!=i2:
ok=True
j1=min(i1,i2)
j2=max(i1,i2)
c1=Permutation_genetic_algorithm.ordered_crossover(p1,p2,j1,j2)
c2=Permutation_genetic_algorithm.ordered_crossover(p2,p1,j1,j2)
return c1,c2
def ordered_crossover(p1,p2,j1,j2):
n=len(p1)
c=[None]*n
for j in range(j1,j2+1):
c[j]=p1[j]
h=0
for j in range(n):
if p2[j] not in c:
assert(c[h]==None)
c[h]=p2[j]
h+=1
if h==j1:
h=j2+1
return c
def do_mutation(self,children):
for c in children:
if np.random.random()<self.pmut:
Permutation_genetic_algorithm.perform_exchanges(c,1)
def perform_exchanges(c,ns):
for i in range(ns):
ok=False
while not ok:
i1=np.random.randint(1,len(c)-1)
i2=np.random.randint(1,len(c)-1)
if i1!=i2:
ok=True
c[i1],c[i2]=c[i2],c[i1]
def select_new_population_best(self,children,g):
'''
Ricapitolando:
Ho messo insieme i padri (self.population) e i figli.
Ho calcolato la funzione obiettivo per ogni figlio.
Ho messo insieme, in un'unica lista, le funzioni obiettivo dei padri (che già avevo) e dei figli.
Ho creato una lista che contiene gli indici di tutti (sia padre che figli):
- i padri hanno un indice che va da 0 a num_elem-1
- i figli da num_elem in poi
Ho ordinato questa lista di indici in base al valore della funzione f.
Ho preso la prima parte di questi indici.
Ho ricostruito la nuova popolazione prendendo i valori di l soltanto per indici migliori e i valori di f.
Infine ho chiamato la funzione update_best.
Questo meccanismo in generale si potrebbe usare come select new population anche per i problemi binari.
'''
l=self.population+children
fc=[self.problem.objective_function(c) for c in children]
f=list(self.f_obj)+fc
l1=list(range(2*self.num_elem))
l1.sort(key=lambda i: f[i])
l1best=l1[:self.num_elem]
self.population=[l[i] for i in l1best]
self.f_obj=[f[i] for i in l1best]
self.update_best(self.population[0],self.f_obj[0],g)
def select_new_population_elit(self,children,g):
# find the best among the children and the parents
f_child=np.array([self.problem.objective_function(c) for c in children])
ib1=np.argmin(self.f_obj)
ib2=np.argmin(f_child)
# first case: the best child is better than the the best parent
if f_child[ib2]<self.f_obj[ib1]:
self.population=children
self.f_obj=f_child
self.update_best(children[ib2],f_child[ib2],g)
else:
iw=np.argmax(f_child)
children[iw]=self.population[ib1]
f_child[iw]=self.f_obj[ib1]
self.population=children
self.f_obj=f_childÈ comunque possibile ottimizzare i vari parametri come pCross e pMut per avere i migliori risultati.
È inoltre consigliato fissare un seed per rendere i risultati riproducibili.
Non sempre la migliore soluzione è generare istanze di cui la soluzione non è nota, un'opzione migliore potrebbe essere quella di utilizzare istanze preparate appositamente per vedere se si raggiunge la soluzione ottima o quanto ci si avvicina ad essa. Per questo è disponibile una libreria apposita, come già detto, contente istanze per il problema del TSP.
Si possono anche osservare le curve di convergenza, plottandole. Per vedere delle prove, fare riferimento all'apposito file di test.
- N -> dimensione della popolazione
- maxgen -> numero di generazioni
- pCross -> probabilità di Crossover
- pMut -> probabilità di Mutazione
N dimensione della popolazione
Che effetto ha aumentare la dimensione della popolazione?
È chiaro intiutivamente che più la popolazione è piccola e minore è la ricchezza del patrimonio genetico (una popolazione piccola è più soggetta alla perdita di diversità in modo molto veloce). Allo stesso modo è chiaro che N influenza il tempo di esecuzione dell'algoritmo.
- Quando N è piccolo, il rischio di perdere diversità è molto alto -> non c'è più evoluzione
- Quando N è alto, il tempo di computazione cresce (il tempo di calcolo è proporzionale a N)
- I GA non sono così sensibili ai valori di N, tranne quando N è troppo piccolo
- In genere si sceglie N in modo da essere proporzionale alla dimensione del problema
maxgen Numero di generazioni
Influenza direttamente la terminazione.
Se lo faccio terminare troppo presto, è probabile che le soluzioni trovate non siano buone. Anche questo parametro dipende dalla dimensione del problema.
Solitamente un buon valore per max-gen può essere calcolato dalla dimensione del problema
- Idea generale: più è grande la dimensione del problema, più è grande lo spazio di ricerca e quindi servono più generazioni.
- Quindi: problem size -> search space size -> number of generation needed
pCross probabilità di Crossover
È la probabilità di utilizzare l'operazione di Crossover su una coppia del mating pool.
Normalmente pCross è alta -> tra 0.8 e 1
pMut probabilità di Mutazione
Nelle stringhe di bit è la probabilità di mutare il singolo gene (se muto ogni singolo gene in maniera indipendente, allora possiamo fare una singola mutazione per genere che deve essere mutato).
Nel TSP invece non c'è il discorso dei geni (perchè si ha a che fare con permutazioni), ma il discorso dei cromosomi (io quindi devo specificare quanto mutare il cromosoma. Quanto lo muto? Nella nostra implementazione si considerava il numero degli scambi).
pMut è la probabilità di mutare il gene/cromosoma
Nelle permutazioni non si può fare la mutazione a livello di gene perchè non si può alterare un singolo elemento della permutazione.
NOTA: Nelle permutazioni, l'operatore di Mutazione deve essere applicato all'intera permutazione e non ad un singolo gene.
Esempio:
0 5 1 4 3 2
Qualsiasi individuo che metto al posto di 1, produce una lista che non è una permutazione!
- La Mutazione è necessaria (nell'esempio del TSP se si mette pMut=0 si rimane bloccati alle prime iterazioni) perchè senza di essa non c'è evoluzione (o ce ne è veramente poca). Il motivo è che la mutazione è l'unico modo per introdurre del materiale genetico non esistente.
- Quando la Mutazione è troppo forte, produce degli individui che sono molto diversi dallo standard della popolazione.
Un buon valore per la probabilità di mutazione è tendenzialmente basso, es:
0.01; 0.001; 0.02
Nonostante deve essere bassa, la Mutazione deve comunque essere presente.
- Generazionale
- I figli vanno al posto dei genitori
- Non importa quanto sono peggio o meglio dei genitori
- Elitismo
- Conserva il migliore individuo della popolazione, o i migliori individui
- I migliori individui tra i genitori e i figli
Negli algoritmi genetici si privilegia l'elitismo o il far sopravvivere i migliori (punto 3).
In generale l'elitismo funziona abbastanza bene. Favorisce uno svecchiamento della popolazione.
- L'elitismo può rinnovare la popolazione senza perdere i migliori individui. Qui vince l'età.
- Selezionare i migliori n individui tra i genitori e i figli solitamente funziona meglio. Qui ha la meglio la fitness (più gli individui sono buoni più sopravvivono).
- Questo meccanismo ha più proabilità di bloccarsi perchè possono rimanere sempre gli stessi individui
Si può vedere la differenza tra l'elitismo e la scelta dei migliori n individui nel problema del TSP in cui sono state implementate entrambe le versioni per la scelta della nuova popolazione. Per maggiori informazioni vedere il codice di permutation_genetic_algorithm.py.
Caratteristiche implementative
Supponiamo di avere due o più metodi per fare la stessa operazione (ad es. selezione dei migliori e selezione per elitismo). Dal punto di vista implementativo conviene fare due classi (che non contengono l'intero algoritmo ma i due codici).
Esempio sulla selezione (elitismo e migliori):
- classe che implementa la selezione:
class selection_best: def __call__(self, pop, children): #call permette di vedere l'oggetto di questa classe come se fosse una funzione #implement the selection # i migliori individui trai i genitori e i figli
- Fare stessa cosa per l'altro metodo:
class selection_elite: def __call__(self, pop, children): # implement the elitism selection
Si hanno quindi due classi che si possono utilizzare come se fossero due funzioni.
Nell'algoritmo genetico:
class gentic_algorithm:
def __init__(self, problem, num_elem, pCross, pMut, . . ., sel_method):
.
.
.
.
.
if sel_method == 'best':
self.selection = selection_best()
elif sel_method == 'elite'
self.selection = selection_elite()
def run(self):
self.selection(self.population, children) # invoca il metodo scelto nel costruttoreQuesta cosa può essere fatta in più linguaggi di programmazione oltre a python.
È raccomandato utilizzare questo design pattern per tutte le alternative del nostro algoritmo. In questo modo è possibile controllare l'esecuzione da riga di comando, non c'è bisogno di duplicare il codice ed è veloce.
Ci sono molti operatori di crossover e mutazione. Per esempio, una permutazione può essere mutata con un'inserzione
In particolare, ci sono alcuni operatori di crossover studiati appositamente per il TSP.
(applicazione degli algoritmi genetici ad un problema vincolato)
vincolato = ho uno spazio di ricerca ottenuto partendo da uno spazio di ricerca più ampio e poi elimando alcune soluzioni.
Spazio di ricerca:
X = {x ∈ Y: x soddisfa una condizione C}
Y spazio di ricerca più grande.
Esempio:
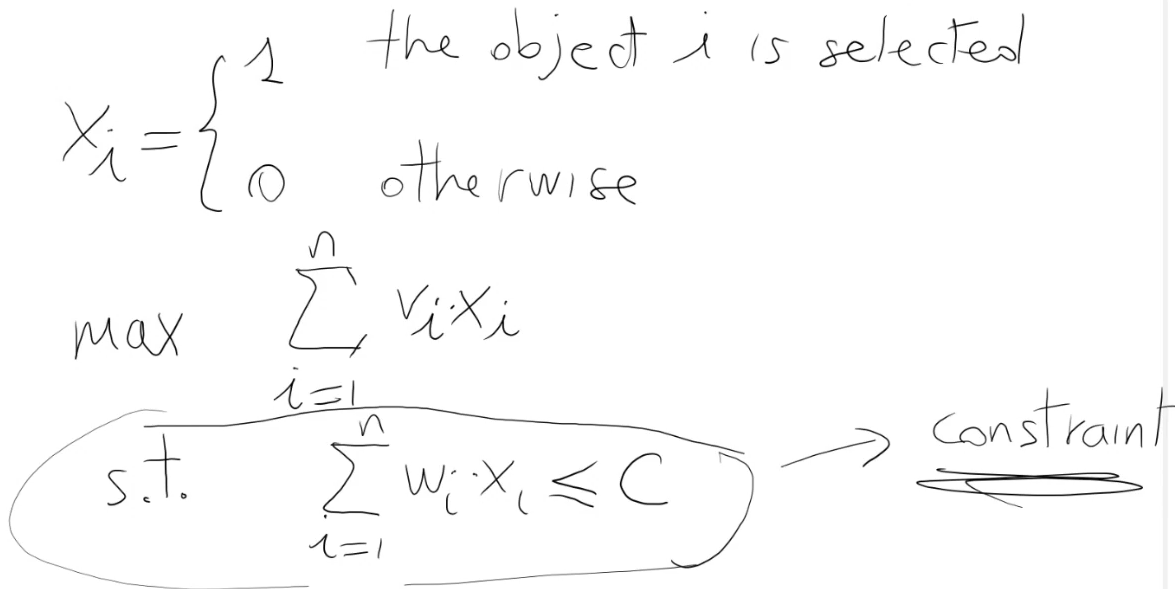
0-1 Knapsack
- n oggetti 1, 2, . . ., n
- ogni oggetto ha un peso
$w_1, w_2, ..., w_n$ - ogni oggetto ha un valore
$v_1, v_2, ..., v_n$ - Zaino con capacità C in kg
L'obiettivo è trovare la composizione ottimale:
Seleziona qualche oggetto tale che la somma dei pesi (sommatoria pesi) è <= C e la somma dei valori (sommatoria valori) è massima.
È possibile ricondurre questo problema ad un problema binario.
Rappresentazione come un vettore binario
Tutte le stringhe di n-bit possono essere ammissibili:
o non ammissibili:
In generale una soluzione per un problema vincolato è ammissibile se rispetta i vincoli.
Negli algoritmi genetici si hanno due possibilità per quanto riguarda le soluzioni da considerare nella popolazione:
-
Non ammettere soluzioni non ammissibili nella popolazione.
- Serve un meccanismo che quando inizializza la popolazione, crea solo soluzioni ammissibili
- Il crossover e la Mutazione devono generare solo funzioni ammissibili
Ci sono problemi di ottimizzazione in cui è difficile perfino creare soluzini ammissibili ed è ancora più difficile garantire che crossover e mutazione producano soluzioni ammissibili.
Si consideri che il 1-point crossover non funziona sulle permutazioni.
Vediamo come è possibile invece risolvere il problema del knapsack con un algoritmo genetico.
-
Ammettere soluzioni non ammissibili.
Una soluzione non ammissibile è una soluzione che non risolve il problema, tuttavia potrebbe non essere lontana dall'essere ammissibile. Di conseguenza valuto quanto è lontana dall'essere ammissibile.
funzione obiettivo (come fitness) -> invece di fare max f(x), faccio max f(x) - k * p(x)
dove p rappresenta la penalità.
p(x) = 0 se x è ammissibile
altrimenti p(x) quantifica "quanto x è distante dall'essere ammissibile".
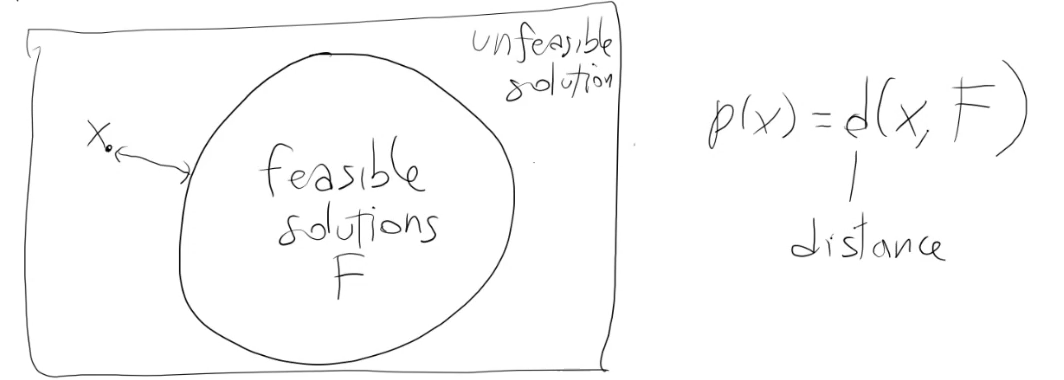
La valutazione della funzione obiettivo è quella considerando la penalità.
Per implementare il secondo approccio, è necessario utilizzare:
- problem.objective_function(x) - penality_coefficient * problem.penalization(x)
per valutare gli individui della popolazione.
k = penality_coefficient, deve essere grande abbastanza per far si che la penalità sia minore del minimo valore di f(x), quando x è ammissibile.
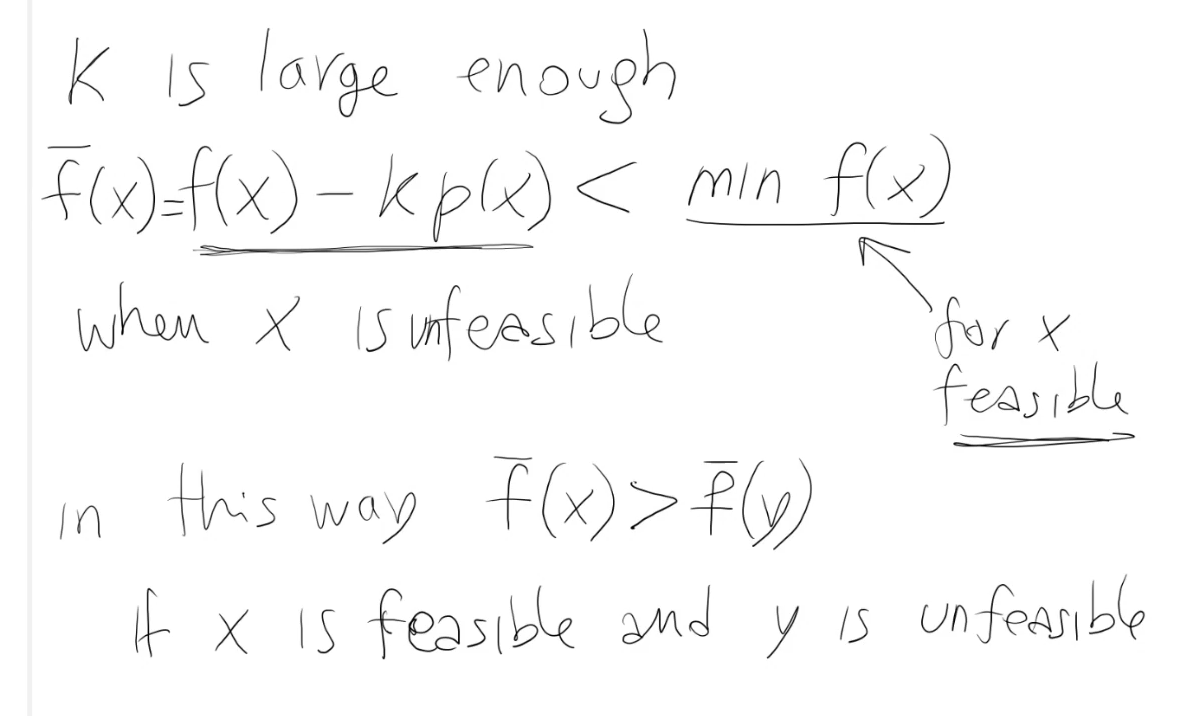
In altre parole x è sempre meglio di y (una soluzione ammissibile è sempre meglio di una soluzione non ammissibile).
Ricordare che la fitness function utilizzata ad esempio nella roulette wheel deve essere positiva (aggiungere una costante a f(x) segnato).
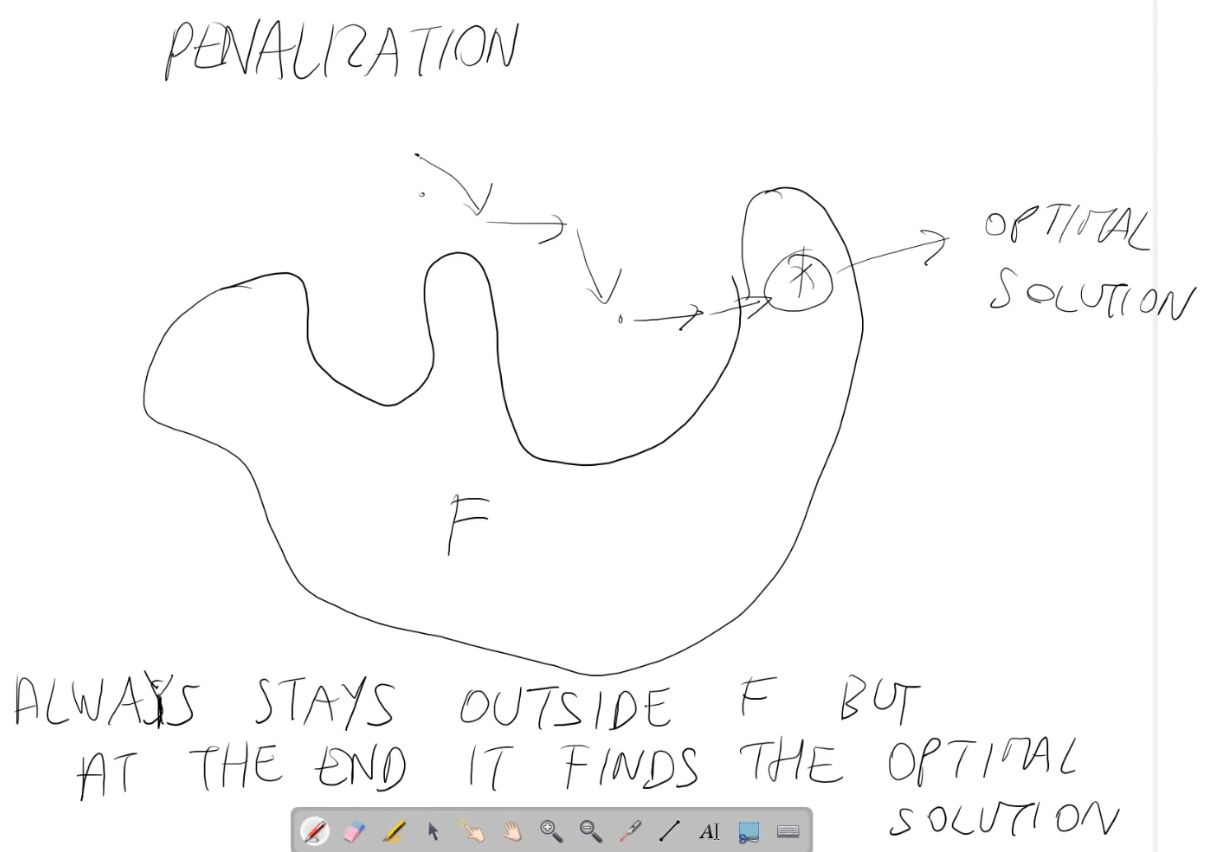
Il principio dietro la penalizzazione è che all'inizio le soluzioni potrebbero essere tutte non ammissibili, ma pian piano emergono soluzioni ammissibili. Le soluzioni ammissibili diventano sempre più presenti nella popolazione, perchè l'algoritmo genetico privilegia le soluzioni ammissibili nella popolazione e prova a ridurre il "gap di non ammissibilità" (penalità).
Questo metodo si può sempre utilizzare per risolvere problemi di ottimizzazione vincolati. I due criteri generali sono:
- Definisci una funzione di penalizzazione per quantificare la non ammissibilità (ovvero per valutare soluzioni ammissibili)
- Trovare il valore per k
Tuttavia, è necessario calcolare f anche se x non è ammissibile. Quando questo non è possibile, si può definire così:
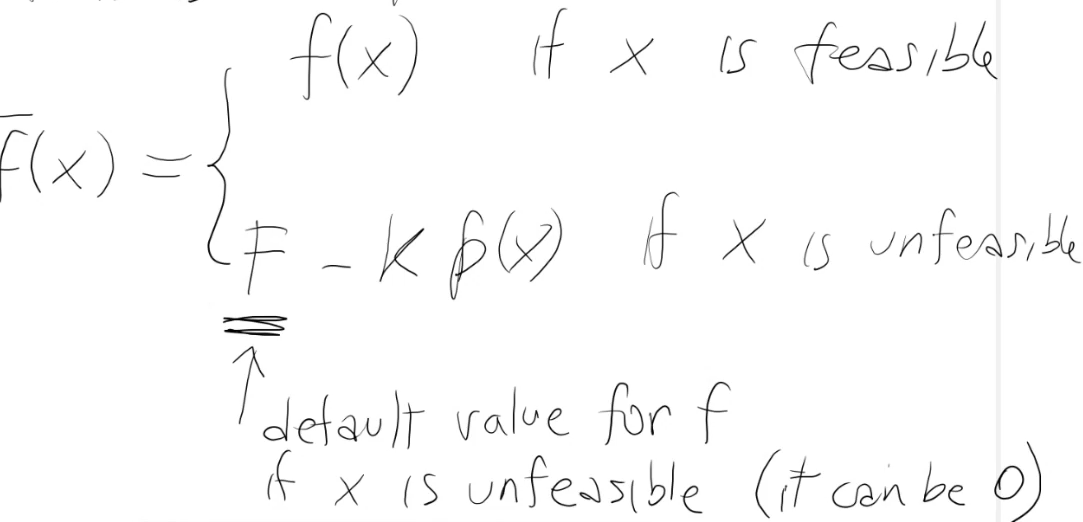
Non è possibile calcolarlo quando ad esempio f non è definito.
Esempio
x deve essere diverso da 0. Che succede se x è 0 ? È un vincolo e in questo caso f non è calcolabile.
Questo non è l'unico modo, c'è un altro approccio: riparare le soluzioni non ammissibili.
Riparare = utilizzare un metodo che parte da una soluzione non ammissibile y e produce una soluzione ammissibile x, effettuando il minor numero possibile di modifiche su y.
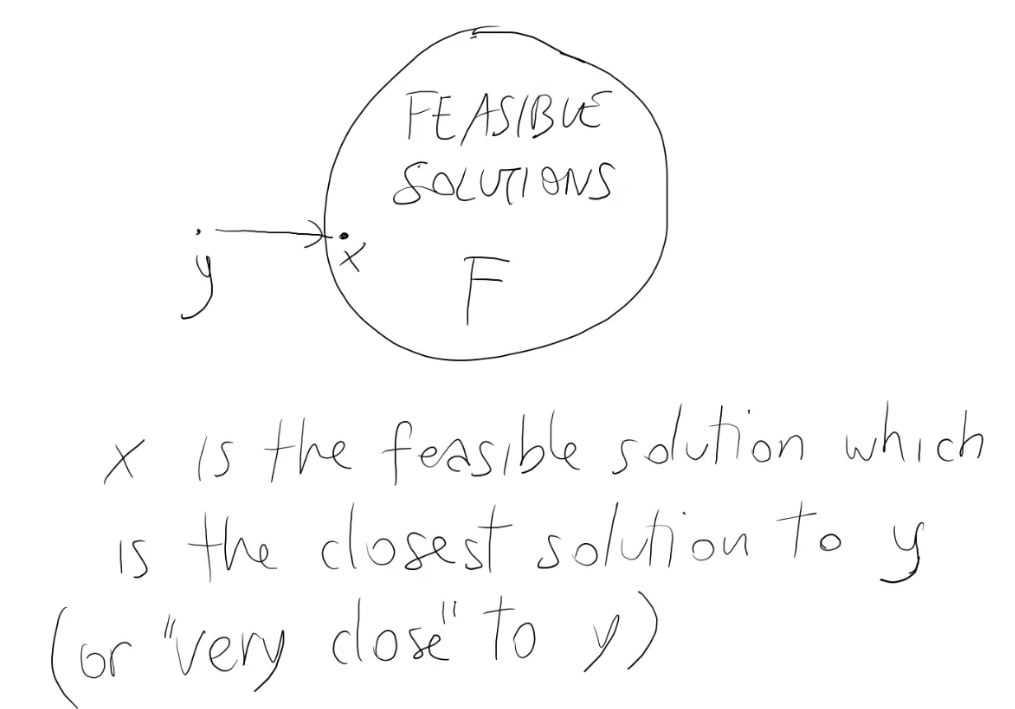
Nell'inizializzazione:
for N individuals
generate a random solution
if not feasible, repair it
evaluate it
Nel ciclo principale si ha uno step in più (riparazione):
CROSSOVER
MUTATION
REPAIR IF UNFEASIBLE
EVALUATION
Per il problema dello zaino, un meccanismo di riparazione ragionevole (basso costo computazionale) per le soluzioni non ammissibili x:
- Rimuovi alcuni oggetti da x, finchè x non diventa ammissibile
$\sum w_i x_i \leq C$
Posso scegliere gli oggetti da rimuovere secondo diversi criteri (randomico, secondo un ordine, rapporto peso/valore ecc...) - Aggiungi alcuni oggetti a x, fintanto che x rimane ammissibile.
Il meccanismo di riparazione dipende dal problema (dipende dalla forma dei vincoli).
Definire un operatore di riparazione è molto più difficile dello scrivere una funzione di penalizzazione.
- La penalizzazione porta il GA a cercare soluzioni ammissibili (che possono, soprattutto inizialemente, non esserlo). Le generazioni sono più veloci.
- La riparazione porta il GA a lavorare sempre con soluzioni ammissibili (minor spreco di calcolo per effettuare generazioni, in quanto ne vengono effettuate di meno. Tuttavia può essere più pesante dal punto di vista computazionale l'effettuare le riparazioni)
Ci sono anche altre alternative alla riparazione e alla penalizzazione:
Scartare le soluzioni non ammissibili: nell'inizializzazione, ogni volta che genero una soluzione non ammissibile, la rigenero. Quando crossover e mutazione producono una soluzione non ammissibile, non la metto nella lista dei children.
Nella fase di inizializzazione si looppa finche N soluzioni ammissibili non vengono create (non strettamente necessario).
Nel main loop non vengono memorizzate soluzioni non ammissibili nella lista dei children.
La penalizzazione ritiene che tutti gli individui siano utili nell'evoluzione, anche quelli non ammissibili. In quanto è possibile trovare soluzioni ammissibili partendo da soluzioni non ammissibili.
continua = opposto di discreta
L'obiettivo è (come per l'ottimizzazione discreta) trovare x* ∈ D tale che f(x* ) è massimo (o minimo).
Un elemento di D è un elemento di d numeri reali.
Per usare un algoritmo genetico è possibile discretizzare il problema, utiizzando p bits per rappresentare un numero reale. Quindi una soluzione potrebbe essere rappresentata come stringa di p x d bits.
In linea teorica è quindi possibile applicare un algoritmo genetico per ottimizzare f.
L'ottimizzazione di una funzione continua è più facile in generale rispetto ad ottimizzare una funzione discreta.
Come mai?
Matematicamente, se io mi muovo in uno spazio continuo e sono in x, se mi muovo di un Δ piccolo:
from x to x + Δx
f(x) -> f(x + Δx) ≈ f(x)
La differenza |f(x+ Δx) - f(x)| può essere piccola
Perche è più facile?:
-
Prima motivazione:
se f è differenziabile, è possibile utilizzare algoritmi molto efficienti di ottimizzazione, basati sul gradiente di f (gradiente = vettore delle derivate).
Il gradiente di f in un punto x ∈ D da un'informazione su quale è la direzione in cui la f cresce e decresce.
Calcolare il gradiente aiuta gli algoritmi, in quanto quest'ultimi sono guidati dal gradiente.
L'algoritmo più famoso basato sul gradiente è: "L'algoritmo di discesa del gradiente" (per la minimizzazione -> è utilizzato per allenare le reti neurali).
Esistono anche molti altri algoritmi basati sulle derivate. Tuttavia questi algoritmi trovano sempre un minimo locale, perchè questi algoritmi nel minimo locale hanno gradiente = 0.
-
Seconda motivazione:
Ci sono degli algoritmi di ottimizzazione chiamati "derivative-free", i quali possono trovare il minimo o massimo globale di f in modo efficiente. Esempi (già implementati nella libreria scipy di python):- Nelder-mead;
- Poquel;
- LBFGS;
- ecc...
Se f è lineare e D è definito in termini di vincoli lineari, il problema di ottimizzare f si chiama problema di programmazione lineare.
- Per spazi discreti, è un problema NP-HARD.
- Per spazi continui, c'è un algoritmo che risolve il problema in tempo polinomiale.
L'utilizzo di algoritmi genetici e altri algoritmi evolutivi per l'ottimizzazione continua è giustificata nelle seguenti situazioni:
- Ci sono dei problemi dove gli algoritmi evolutivi trovano soluzioni migliori rispetto agli algoritmi classici. Questo per esempio per problemi in cui la funzione obiettivo f ha molti minimi (o massimi) locali. Oppure quando l'obiettivo non è trovare più minimi (o massimi).
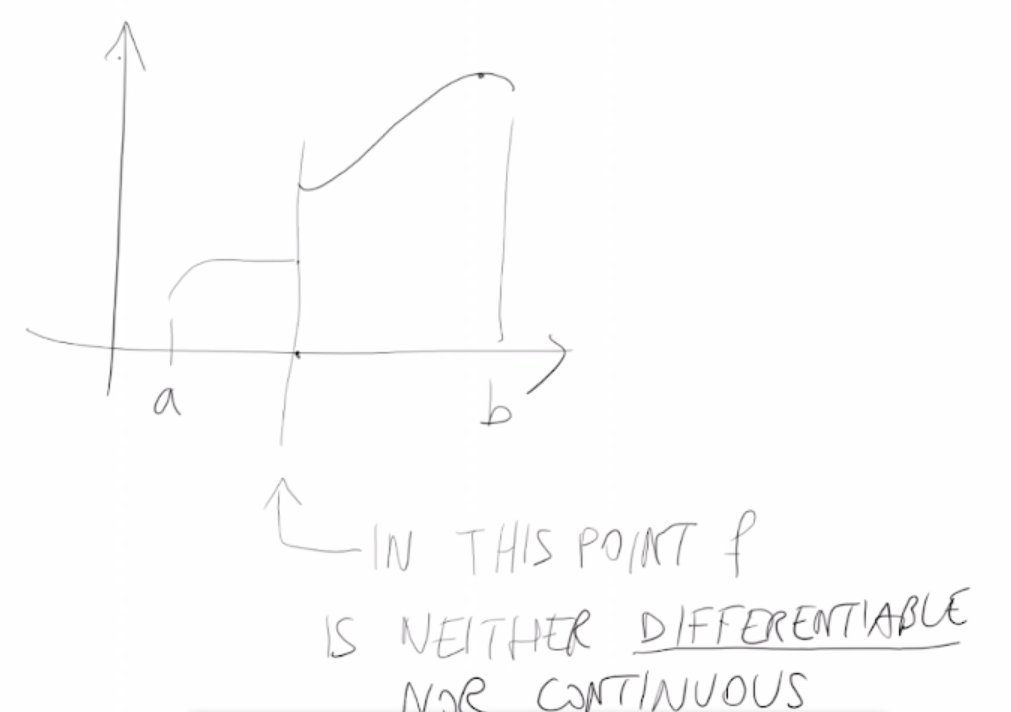
- Quando f non è esattamente una funzione continua. Ci sono due possibilità:
Altre situazioni in cui sono utilizzati gli algoritmi evolutivi in problemi di ottimizzazione continua:
- f è dinamica -> f cambia nel tempo -> Dinamicità
- f è alterata dal rumore esterno (la f quando viene valutata non è esatta, potrebbe quindi succedere che valutando la f nello stesso punto ritorna valori diversi. Un algoritmo tradizionale non riuscirebbe ad andare avanti o ad esempio calcolarsi il gradiente, a differenza degli algoritmi evolutivi.) -> Casualità
Le strategie evolutive (ES) sono algoritmi iterativi in cui ad ogni generazione viene valutata una popolazione in base alla fitness.
x <-- random point in D
z <-- f(x)
for g <-- 1 to max_gen
ε <-- random vector of dimension d
x' <-- x + ε # è una sorta di mutazione
z' <-- f(x')
if z' <= z
x <-- x'
z <-- z'
return x, z
Come viene generato il vettore ε ?
ε può essere generato usando una distribuzione normale di dimensione d.
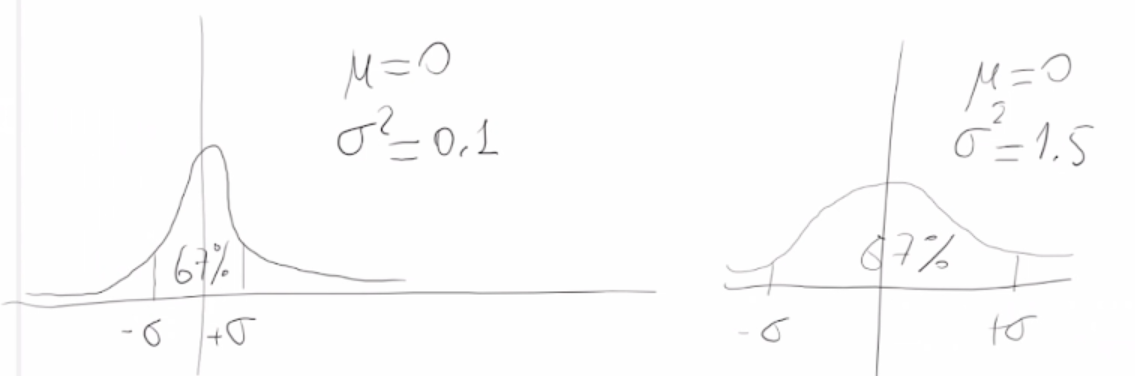


Tutte le componenti di ε sono indipendenti (le estraggo indipendentemente dalle altre).
Per estrarre ε si può fare così:
eps = np.zeros(d)
for in range(0,d):
eps[i] = random.normal(0, sigma2)Lo schema evolutivo precedenete non fa utilizzo di una popolazione.
La popolazione può essere introdotta dal seguente schema di generalizzazione:
Crea µ figli da λ genitori.
λ = dimensione della popolazione
μ = numero di figli
λ < μ
for i <-- 1 to λ
generate xi
for g <-- 1 to max_gen
for i <-- 1 to μ
generate x'i by manipulating some xj
select the best λ individuals among the children as new value x1, ..., xλ for next iteration # Non c'è elitismo
return the best individuals ever found
La selezione avviene solo tra i
Un'altra alternativa è di utilizzare:
La selezione prende i migliori λ individui tra i genitori e i figli. I migliori λ individui tra padri e figli sopravvivranno e diventeranno genitori nella generazione successiva. Quindi anche i genitori possono partecipare alla selezione per la generazione successiva.
- λ = 1 e μ = 1 --> (1+1)-ES
- λ > 1 e μ = 1 --> mutare un individuo tra la popolazione o scelto secondo qualche
criterio come tornei o roulette wheel.
L'unico figlio può sostituire il peggiore della popolazione. - λ > 1 e μ > 1 --> caso generale
Parametri di una ES (evolutionary strategies):
- λ
- μ
-
$\sigma^2$ (o in generale Σ)
Le strategie evolutive possono usare anche meccanismi per adattare
- rule 1/5 : adatta σ in modo da mantenere la percentuale di mutazione con successo intorno a 1/5
Mutazione con successo = genero un individuo che è migliore. La mutazione se io genero un x' la cui f è migliore di x. - Un'altra tecnica è assegnare ad ogni individuo un valore per σ

È una delle strategie evolutive più performanti.
E una versione moderna ed estesa delle strategie evolutive. Qui la mutazione è fatta prendendo un vettore casuale r[i] secondo la distribuzione normale con medie m e matrice di covarianza C. L’algoritmo aggiorna m e C ad ogni iterazione tramite i risultati finora ottenuti. Le formule per l’aggiornamento
sfruttano la statistica e algebra lineare.
Non fa utilizzo della popolazione, al suo posto fa uso di un modello probabilistico.
Invece di generare μ figli dalla popolazione (ad esempio tramite mutazione), i figli sono campionati dal modello M.
Il modello probabilistico utilizzato è un modello Gaussiano (utilizza la distribuzione normale) con n come vettore delle medie.
genera i valori iniziali per i parametri di M
for g <-- 1 to max_gen
genera μ individuo da M # utilizzare un generatore di numeri pseudo casuali da M e estrarre μ individui x1, ... , xμ
scegliere i migliori λ individui
usare x(1), ... , x(λ) per aggiornare i parametri di M
return il miglior individuo
Aggiornare i parametri di M dovrebbe produrre individui sempre migliori (non è certo). L'idea è che l'aggiornamento dovrebbe spingere sia la media che la varianza della popolazione verso individui buoni.
CMA-ES aggiorna i parametri m e c attraverso delle formule matematiche basate sull'algebra lineare.
È uno dei metodi più utilizzati in assoluto per fare l'ottimizzazione di funzioni continue.
È uno dei migliori e più semplici algoritmi per l'ottimizzazione continua (caratteristiche difficili da trovare combinate insieme). Soprattutto nella sua versione base è sia efficiente che semplice da implementare.
DE è una specie di algoritmo genetico che lavora su vettori (gli algoritmi genetici solitamente lavorano su stringhe. Infatti le operazioni di base come crossover sono operazioni sulle stringhe, stessa cosa la mutazione) e ottimizza un problema tentando iterativamente di migliorare una soluzione rispetto ad una data misura di qualità (funzione di fitness). Non garantisce che venga trovata una soluzione ottimale ed è espressamente pensato per ottimizzare funzioni di variabili reali con moltissimi minimi locali.
Nella sua forma base, chiamata DE/RAND/1/BIN:
- RAND -> perchè la mutazione è fatta casualmente
- BIN -> perchè il crossover è fatto in maniera binomiale
Abbiamo:
- f (objective function)
- d -> dimensione dello spazio (vettori di dimensioni d)
- D -> dominio della funzione f
Per il funzionamento abbiamo bisogno di:
- Una popolazione di N individui v[i];
- Mutazione Differenziale: Per ogni individuo della popolazione v[i] si crea un vettore u[i] mutante.
- Crossover combinatorio: Per ogni coppia (v[i], u[i]) (popolazione, vettore mutato) si crea un nuovo vettore candidato w[i] che prende un pò di elementi da u e da v in base ad un parametro chiamato CR.
- Aggiornamento popolazione: Ogni vettore candidato w[i] sostituisce il corrispondente v[i] se w[i] ha un valore migliore di f.
Crea N vettori iniziali x1, ..., xn (ad esempio in modo casuale)
for gen <-- 1 to max_gen
crea la popolazione di mutanti y1, ..., yn (mediante la mutazione)
crea la popolazione di candidati z1, ..., zn (tramite il crossover)
aggiorna la popolazione
end for
return il migliore elemento ever found
(da notare che l'ordine in cui vengono eseguiti crossover e mutazione è invertito).
Un'altra cosa importante è che gli operatori di crossover e mutazione operano su vettori.
Io devo trovare
for i <-- 1 to N
seleziona tre vettori differenti tra loro r1, r2, r3 e diversi da i
yi <-- xr1 + F * (xr2 - xr3)
#parametro (scalare) differenza tra vettori
somma tra vettori
questa operazione per calcolare y1 corrisponde a:
for j <-- 1 to d
y1[j] = xr1[j] + F * (xr2[j] - xr2[j])
end for
Noi abbiamo
Quindi il crossover prende alcune componenti di
La popolazione è così aggiornata:
for i <-- 1 to N
if f(zi) < f(xi) then
xi <-- zi
end if
end for
Quindi ricapitolando, il Differential Evolution:
- ha un ciclo esterno per max_gen generazioni -> max_gen iterazioni (G = max numero di generazioni), in cui ad ogni iterazione abbiamo:
- Mutazione -> richiede O(N*d) operazioni
- Crossover -> richiede O(N*d) operazioni
- Selezione -> richiede O(N*f_(f segnato)) -> f_ è il costo di calcolare f(zi)
Complessivamente il costo del DE è polinomiale rispetto a G, N, d, f_
Il Differential Evolution può essere usato per l'ottimizzazione numerica ma anche per altri tipi di ottimizzazione.
Il Differential Evolution si può estendere facilmente anche ad altri tipi di problemi:
- ottimizzazione vincolata
- ottimizzazione mista (reali/discreta)
- ottimizzazione combinatoria (DE per le permutazioni)
L'idea del DE è quella di utilizzare due tipologie diverse di operatori genetici:
- mutazione del DE è di tipo vettoriale (sono operazioni vettoriale)
- crossover è di tipo combinatorio (vede i vettori come stringhe).
Il DE lavora sia a livello vettoriale (mutazione) che al livello di stringhe (crossover). Qui si nota già una prima differenza con gli algoritmi genetici, i quali lavorano solo a livello di stringhe.
Altre differenze:
-
Mutazione: normalmente dovrebbe essere un operatore unario (prendo un individuo e lo muto). In questo caso invece, crea un nuovo vettore combinando in modo lineare i tre vettori della popolazione (questo per ogni elemento della popolazione).
Come mai questa cosa?

Con 0 < F <= 2
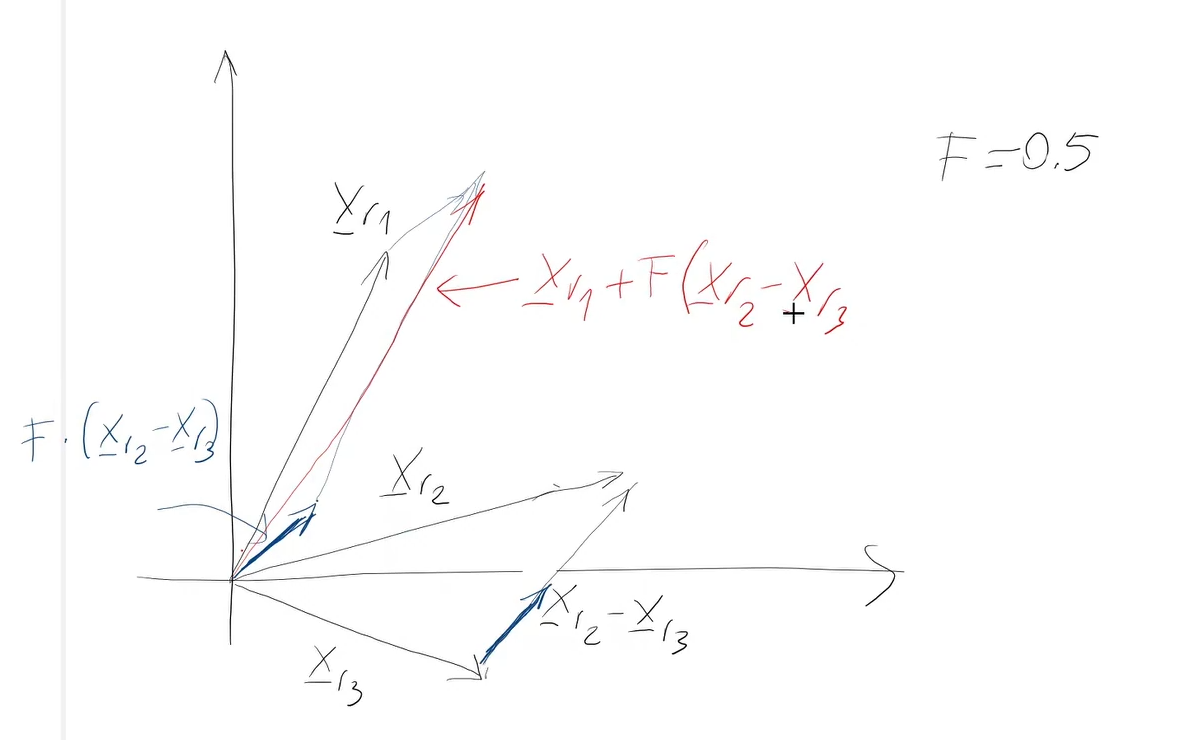
Ora qui di seguito ci sono 2 scenari per capire cosa fa la mutazione:- Soprattutto all'inizio gli elementi (vettori) della popolazione sono molto diversi tra di loro.
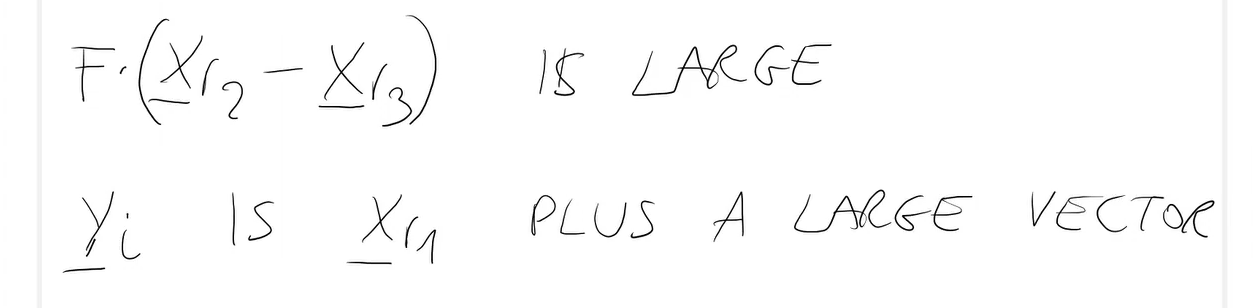
Quindi$y_i$ è probabilmente molto diverso dagli altri elementi (dagli altri vettori). -
Cosa succede se gli elementi della popolazione sono simili tra di loro? (tutti i vettori sono simili tra di loro)
In questo caso succede l'esatto contrario
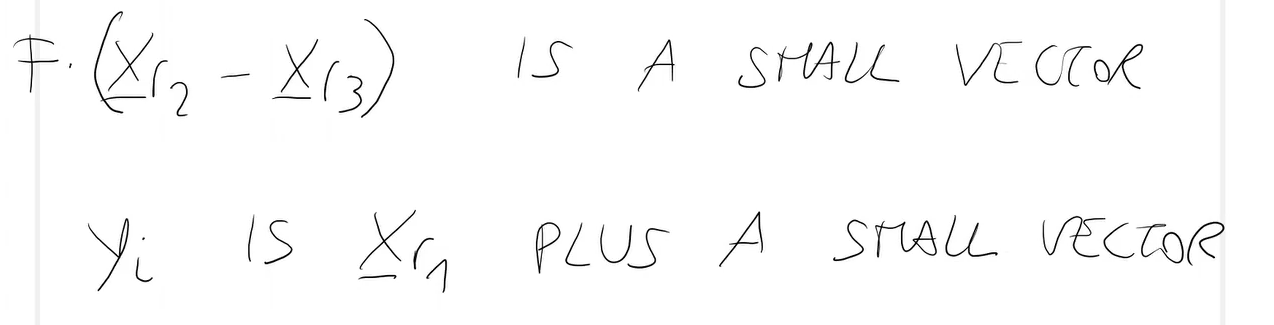
Quindi$y_i$ è vicino a qualche vettore della popolazione.
La DE crea un vettore mutante che dipende da quanto i vettori della popolazione sono differenti tra di loro. Se sono molto differenti, il vettore mutante sarà un vettore a caso e molto diverso dagli elementi della popolazione. Se sono poco differenti, il vettore mutante sarà simile a v[1], e quindi simile ad un elemento della popolazione.
In pratica il DE si autoregola, perchè all'inizio è più probabile che ci si trovi nel primo scenario (quindi la mutazione fa dei salti importanti (exploration) -> prendo degli individui e li muto molto.
Se l'algoritmo invece sta convergendo (gli individui diventano sempre più simili) ci troviamo nel secondo scenario e la mutazione fa piccoli salti (piccole variazioni) (exploitation).
Il DE usa una forma di auto-adattamento nella forza della Mutazione.
La popolazione del DE tende a convergere perchè è automaticamente elitista (il miglior individuo della popolazione rimane sempre).
Tuttavia non c'è un meccanismo in cui sopravvivono tutti i migliori individui, ma ogni individuo è confrontato con un altro, quindi alcuni elementi buoni potrebbero essere scartati (c'è una competizione uno a uno).
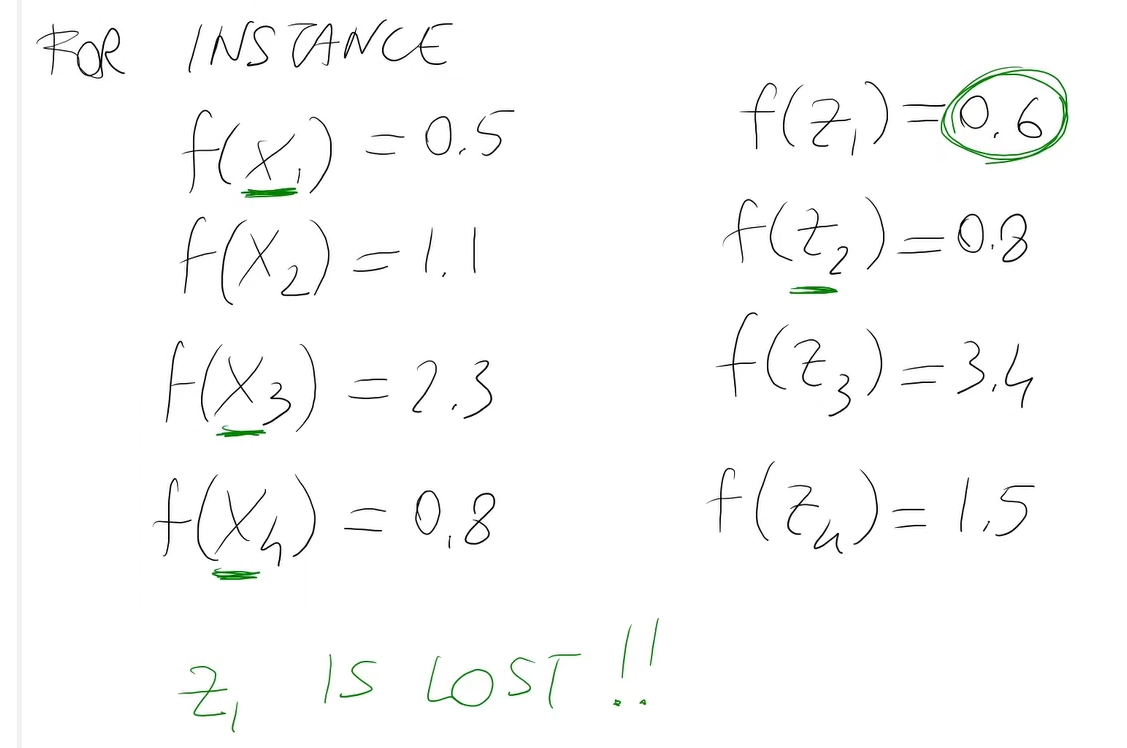
- Soprattutto all'inizio gli elementi (vettori) della popolazione sono molto diversi tra di loro.
# Una semplice implementazione dell'algoritmo Differential Evolution
import numpy as np
class Objective_Function:
def __init__(self, fun, dim, domains):
'''
- fun è la definzione della funzione
- dim è il numero di parametri
- domains è la lista degli intervalli [x_i_min, x_i_max] per ogni variabile x_i
'''
self.fun = fun
self.dim = dim
self.domains = domains
def __call__(self, x):
return self.fun(x)
class Differential_Evolution:
def __init__(self, objf, np, f, cr, max_gen):
self.objf = objf
self.np = np
self.f = f
self.cr = cr
self.max_gen = max_gen
def initialize(self): # Serve ad inizializzare l'algoritmo (Ad esempio è necessario creare i vettori della popolazione)
d = self.objf.dim
self.population = []
self.values = []
for i in range(self.np):
r = np.random.random(d)
for j in range(d):
l, u = self.objf.domains[j] # intervallo della j-esima variabile della funzione
r[j] = l + (u - l) * r[j]
self.population.append(r)
self.values.append(self.objf(r))
self.best_f = 1e300
self.find_best()
def find_best(self):# trovo il miglior elemento della popolazione
self.i_best = 0
for i in range(1, self.np):
if self.values[i] < self.values[self.i_best]:
self.i_best = i
if self.values[self.i_best] < self.best_f:
self.best_f = self.values[self.i_best]
self.best = self.population[self.i_best]
print("found new best with f = {}".format(self.best_f))
def evolution(self):
self.initialize()
for g in range(1, self.max_gen+1):
mutants = self.differential_mutation()
trials = self.crossover(mutants) # gli elementi prodotti dal crossover nel differential evolution si chiamano trials
self.selection(trials)
self.find_best()
return self.best_f, self.best
def differential_mutation(self):
mutants = []
for i in range(self.np):
# RAND/1 implementations
l = [j for j in range(self.np) if j != i]
r1, r2, r3 = np.random.choice(l, 3, replace=False)
m = self.population[r1] + self.f * (self.population[r2] - self.population[r3])
mutants.append(m)
return mutants
def crossover(self, mutants):
trials = []
d = self.objf.dim
for i in range(self.np):
j_rand = np.random.randint(0, d)
tr = np.zeros(d)
for j in range(d):
if np.random.random() < self.cr or j == j_rand:
tr[j] = mutants[i][j]
else:
tr[j] = self.population[i][j]
trials.append(tr)
return trials
def selection(self, trials):
for i in range(self.np):
fx = self.objf(trials[i])
if fx < self.values[i]:
self.population[i] = trials[i]
self.values[i] = fxPer quanto riguarda il codice completo e i comandi per testare l'algoritmo vedere nell'apposita directory in cui è riportata l'implementazione dell'algoritmo DE.
Successivamente ai test con questo primo esempio:
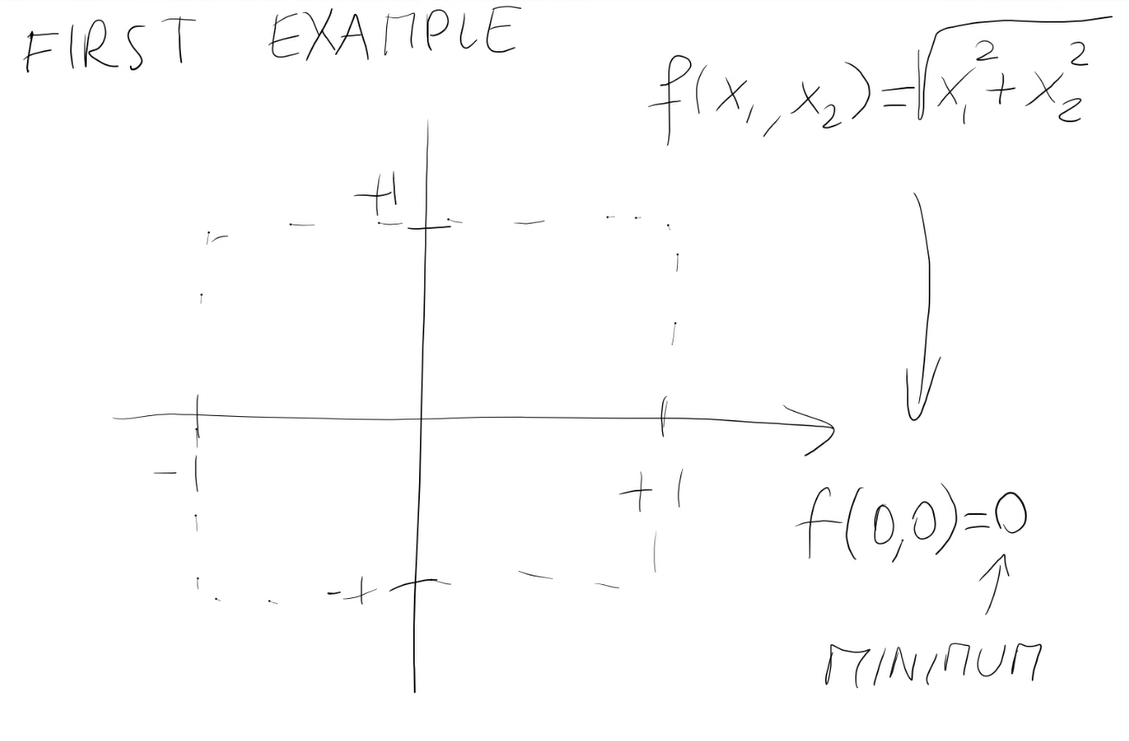
, è possibile effettuare dei test cambiando il tipo di funzione con cui si ha a che fare. Un esempio è la funzione RASRIGIN (la quale è difficilmente ottimizzabile utilizzando la tecnica di discesa del gradiente, a differenza del DE con la quale si riesce ad ottimizzare abbastanza bene).
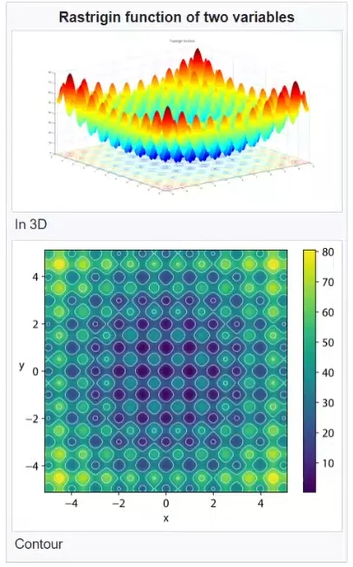
Fino ad ora abbiamo visto che:
- (RAND/1)
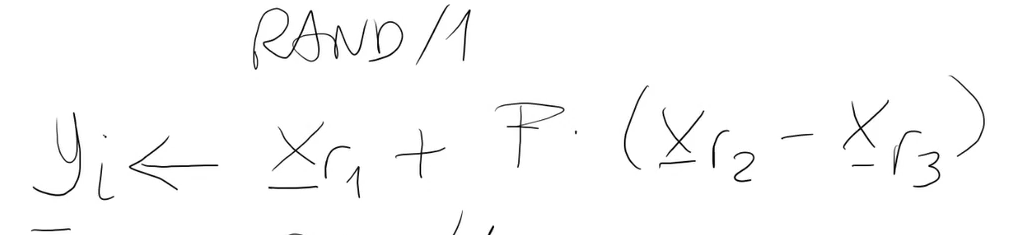
- (BEST/1)

In pratica anzichè scegliere come base della mutazione un elemento a caso, sceglie l'elemento migliore della popolazione. Questa variante converge più velocemente. Vi è tuttavia un rischio che quest'ultima si stabilizza prima (potrebbe essere una scelta non molto sensata). - (RAND/2)
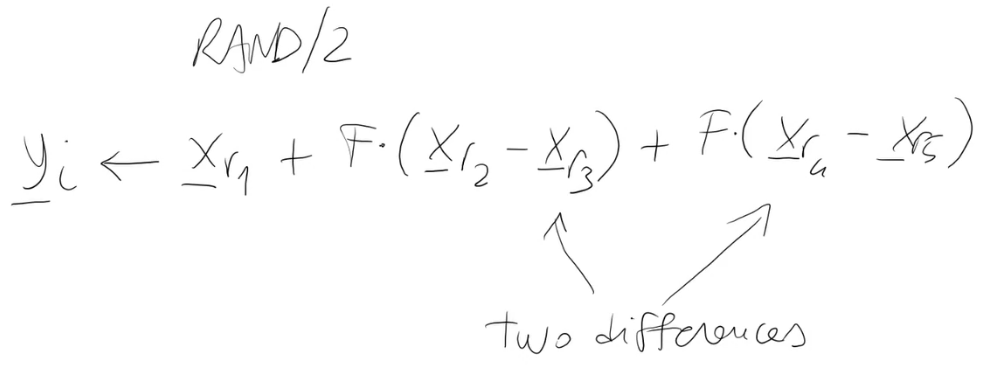
Significa che ho due differenze, anzichè una sola (si è meno legati al caso).
Ci sono tante altre varianti:
- Current-to-Best

Questa si usa senza crossover, perchè xi è già dentro la formula -> yi dipende anche da xi.
Quali sono i corretti valori per f e cr? Esistono molti metodi per assegnare i valori di f e cr (che sono i valori più complicati da controllare).
- Le implementazioni più semplici utilizzano dei valori fissi
- Ma ci sono due approcci migliori:
- Utilizzare una strategia fissa per modificare f e cr.
Inizialemente si hanno dei valori alti per f e cr e poi scendono mano a mano (inizialmente si tende ad esplorare molto) - Self-adapting f e cr.
Si ha un algoritmo che modifica f e cr in base alla risposta della popolazione stessa.
- Utilizzare una strategia fissa per modificare f e cr.
I parametri del DE:
- NP -> dimensione della popolazione
- f -> parametro della mutazione
- cr -> parametro del crossover
- max_gen -> numero di generazioni
Il DE, come altre metaeuristiche, ha diverse varianti in base alle operazioni di mutazione e crossover utilizzate. Ad esempio:
- Varianti sulla mutazione: RAND/1, RAND/2, BEST/1, BEST/2, CURR-TO-BEST, etc...
- Varianti sul crossover: BIN, EXP, etc...
È difficile scegliere quali parametri e quali varianti utilizzare. Ci sono tuttavia delle tecniche che permettono di scegliere in maniera sensata:
- Self-Adapting: l'algoritmo sceglie da solo in maniera automatica, mano a mano che la risoluzione va avanti. L'algoritmo lavora a due livelli, allo stesso tempo:
- cerca la migliore soluzione (rispetto alla funzione obiettivo)
- cerca i parametri/varianti migliori
L'algoritmo contemporaneamente fa evolvere la soluzione del problema (la popolazione) e i parametri di se stesso.
Un semplice schema dell'algoritmo Self-Adapting per f e cr è il jDE schema.
In questo schema, ogni elemento della popolazione comprende:
- un vettore x_i
- un valore f_i
- un valore cr_i
Funzionamento:
Con una certa probabilità
Al passaggio di selezione,
if f(zi) < f(xi) then
xi <- zi e
f_i <- f_i' # se sono diversi
cr_i = cr_i' # se sono diversi
Altre forme del Self-Adapting sono utilizzate in algoritmi Jade e Shaede (sono versioni del DE). Questi algoritmi utilizzano delle tecniche statistiche per evolvere f e cr.
Un altro approccio completamente differente per trovare la migliore combinazione di parametri e varianti (tuning dei parametri) è il Machine Learning:
- Creare un set di combinazioni possibili. Ad esempio f = {0.1, 0.2, 0.5, 0.7, 1, 1.5, 2} e cr = {0.1, 0.3, 0.5, 0.7, 0.9}, qui si hanno 35 possibili combinazioni.
- Crea un insieme di test (che in realtà è un insieme di training) con istanze del problema di ottimizzazione f1, f2, ..., fk
- Eseguire l'algoritmo DE in ogni istanza utilizzando ogni possibile combinazione: 35 combinazioni x 10 istanze x 10 run (essendo un algoritmo stocastico bisogna limitare l'influenza del caso) = 3500 run
- Calcolare per ogni passaggio alcune statistiche sui risultati (ad esempio la media o la mediana)
- Scegliere la combinazione con il miglior punteggio (per esempio la media più bassa)
È simile ad un vero approccio di Machine Learning.
Ci sono tuttavia delle problematiche che possono occorrere:
- Overtuning: La combinazione trovata con questo approccio, dipende fortemente dalle istanze di test. È possibile che le prestazioni su una nuova istanza non siano buone.
- Le performance dell'algoritmo dipendono anche dai parametri iniziali scelti (discretization). Per ridurre il tempo necessario nel tuning:
- si può ridurre il numero di combinazioni, scartando quelle che sembrano poco promettenti.
- selezionare solo istanze rappresentative
In generale la fase di parameter tuning può essere eseguita da dei tools automatizzati (irace, smac, ...), dovendo comunque fornire:
- un insieme di istanze
- insiemi di valori possibili per ogni parametro
Le implementazioni che si trovano nelle principali librerie (nevergrad, scipy.optimize, ...) hanno dei parametri di default per i parametri.
Utilizzare una funzione di decodifica: trasforma un vettore di numeri reali in una soluzione per il problema di ottimizzazione.
Esempio: Risolvere il probelema del Number Partitioning utilizzando il DE
Implementare il DE con degli accorgimenti per fare in modo che ogni vettore è composto da numeri reali in [0, 1].
Nello step di selezione si calcola
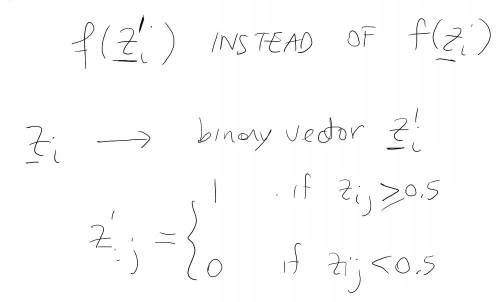
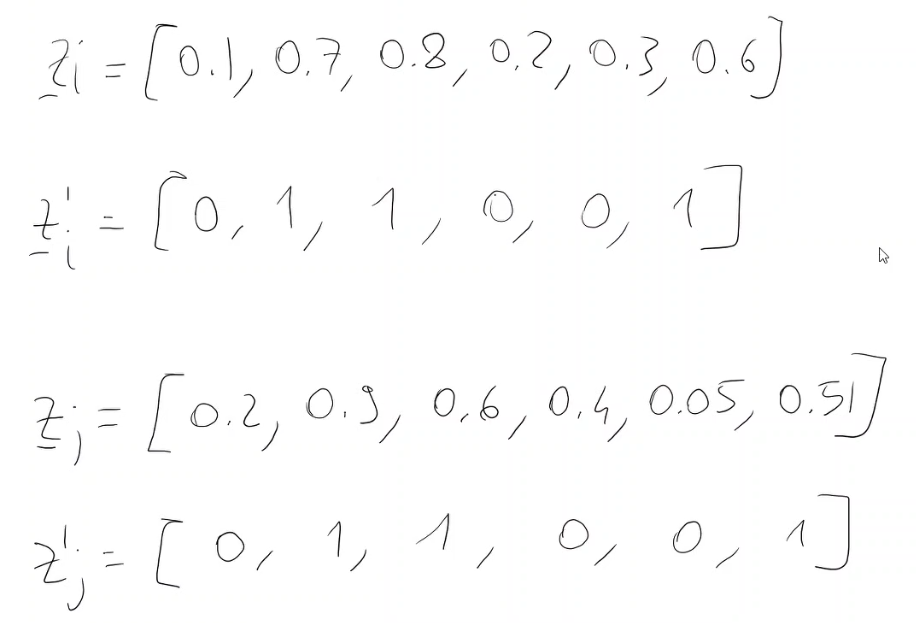
Questo però causa il fatto che infiniti vettori di numeri reali corrispondono alla stessa soluzione per il problema originale.
Questo approccio è sempre applicabile (è sufficiente trovare una funzione di decoding) ma l'intero processo di ricerca è distorto in quanto:
Vettori simili possono corrispondere a soluzioni differenti e vettori molto diversi possono corrispondere alla stessa soluzione.
In generale per risolvere un problema di otttimizzazione discreta è possibile utilizzare:
- Un algoritmo per problemi di ottimizzazione continua
- Una funzione di decodifica
Ad esempio, per risolvere il TSP utilizzando il DE.
Utilizzare la Random Key decoding function (trasformare un vettore in una permutazione).
Un secondo approccio per usare il DE, o altri algoritmi per l'ottimizzazione continua, è di definire operazioni "numeriche" per la soluzione:
- soluzione + soluzione
- soluzione - soluzione
- soluzione * soluzione
La mutazione RAND/1 è interpretata come segue:
yi <-
Nel NPP
I due approcci sono molto diversi:
- Nel primo approccio si fanno evolvere i vettori ma poi i vettori hanno un significato diverso. Il vettore rappresenta l'evoluzione, la soluzione, la valutazione (il vettore è una codifica/decodifica della soluzione)
- Nel secondo approccio si fanno evolvere direttamente le soluzioni, che sono contemporaneamente sia la valutazione che l'evoluzione.
Perchè utilizzare un algoritmo per l'ottimizzazione continua su un problema di ottimizzazione discreta?
Non ci sono così tanti algoritmi per spazi discreti, la maggior parte delle nuove implementazioni si basano su algoritmi continui. Questo perchè è più facile lavorare su spazi continui. La spinta ad utilizzare questi algoritmi nel discreto è che quest'ultimi sono più difficili.
L'inventore della programmazione genetica è John Koza (anni 80). Rappresenta un’estenzione degli algoritmi genetici dove ogni elemento della popolazione rappresenta un programma anzichè una stringa di bit. La popolazione è un insieme di funzioni ed evolve in base ad una funzione di fitness. Gli operatori di crossover e mutazione sono adattati a una rappresentazione ad albero.
- È un algoritmo che fa evolvere una popolazione di programmi.
- g(p) = indica quanto è buono p per il problema che voglio risolvere
Differenza tra un algoritmo genetico e la programmazione genetica: da individui si passa a funzioni
Ad esempio, ho una funzione
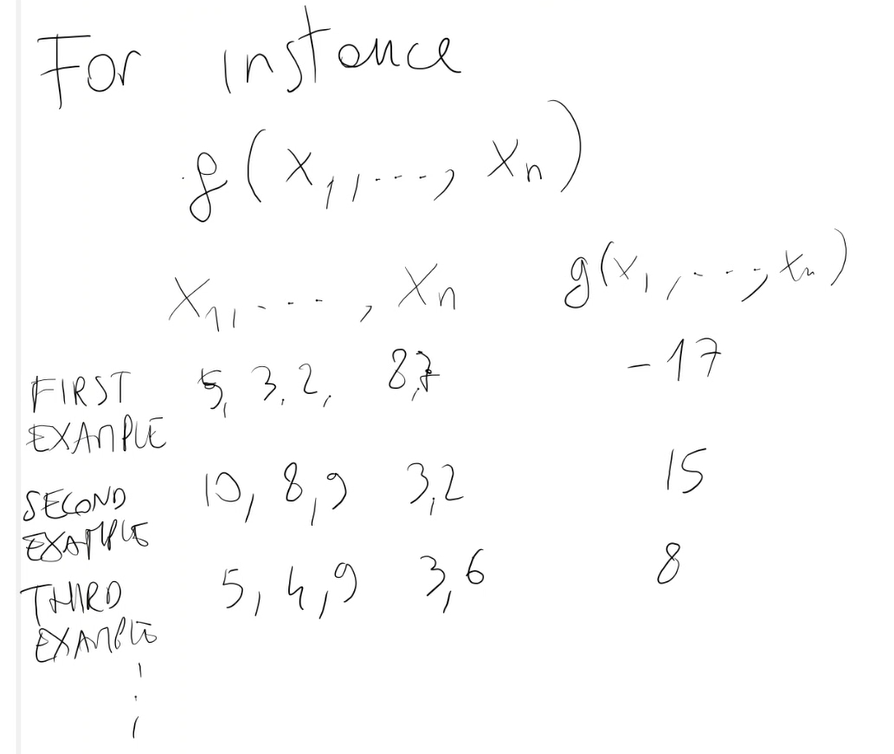
N esempi di g e per ogni esempio di g:
$y^{(i)} = g(x^{(i)}_1, ..., x^{(i)}n)$
L'obiettivo è trovare g
Questo problema è legato alla regressione lineare (la regressione lineare ne è un caso particolare)
$g(x_1, ..., x_n) = a + b_1 x_1 + b_2 x_2 + ... + b_n x_n$
Trovare $a$ e $b_1, ..., b_n$ tale per cui $\sum{i = 1}^{N}[y^{(i)} - g(x^{(i)}_1, ..., x^{(i)}_n)]^2 $ è minima.
Ad esempio la regressione lineare utilizza il metodo dei minimi quadrati.
Questo problema è legato ai task supervisionati del Machine Learning. Supponendo di avere una rete neurale e di volerla addestrare.
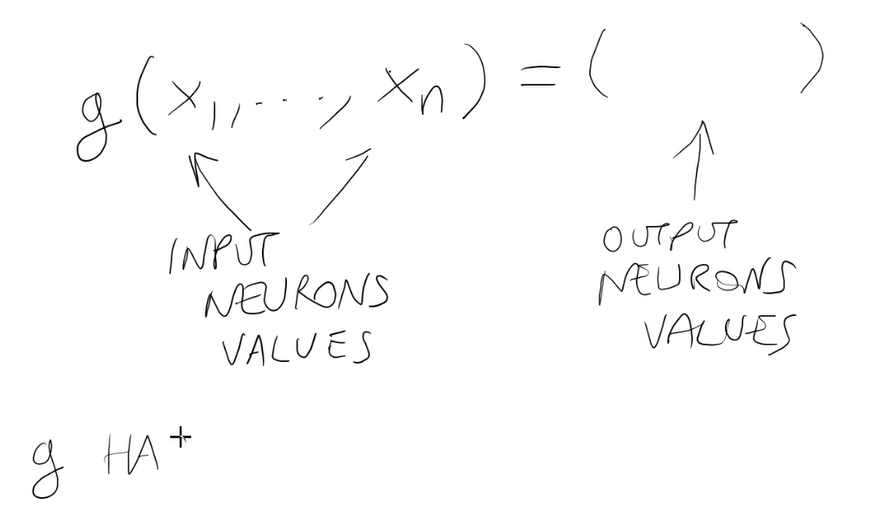
g ha una forma funzionale fissa e l'unica cosa che deve essere trovata sono i valori dei pesi e dei bias.
Ho quindi un training set con N esempi e devo trovare i pesi tali per cui
(somma funzione di perdita)
Nella programmazione genetica g non ha una forma funzionale fissa (io devo imparare la funzione).
L'esempio più semplice di GP (genetic programming) è la regressione simbolica.
Ho un dataset di esempi formato da:
Esempio numerico: voglio trovare che relazione c'è tra:
- y = prezzo di vendita,
-
$x_1$ = anno di costruzione, -
$x_2$ = zona in cui si trova la casa, -
$x_3$ = stato di conservazione.
Voglio costruire un meccanismo che preveda il valore di y in funzione dei valori di
- Usare una rete neurale: il difetto di questo approccio è che quello che otteniamo funziona benissimo, ma la rete non dice niente su quale è la relazione dato il funzionamento a Black Box.
- Usare modelli statistici
- Programmazione Genetica.
La programmazione genetica tenta di trovare una funzione f tale che l’errore che si commette (cioè la differenza tra f(x1, x2, x3) e y) sia il più piccolo possibile. Si usa come nelle reti neurali una funzione di perdita:
GP prova a minimizzare la funzione di loss esattamente come fanno le reti neurali.
La differenza con le reti neurali è che la g la deve trovare l'algoritmo.
Non c'è una forma fissa e l'algoritmo deve trovare i pesi. G può essere qualsiasi espressione e l'algoritmo deve trovarla. Se la funzione di perdita fosse 0 significa che io ho trovato esattamente la funzione (forma funzionale) che genera la
In generale, GP restituisce la migliore g trovata in un dato numero di generazioni (o altri criteri. Ad esempio si potrebbe interrompere l'algoritmo appena trovo una g tale per cui la funzione di perdita sia minore di un certo valore).
GP è un algoritmo genetico che lavora con espressioni o porzioni di codice.
Ci concentreremo su algoritmi che lavorano con espressioni.
- Come prima regola non posso trattare un'espressione come stringa.
Ad esempio, con il crossover ad un punto (one-point crossover) se tratto le espressioni come stringhe si creano elementi che non hanno senso. Esempio se io taglio dopo i primi 4 caratteri:
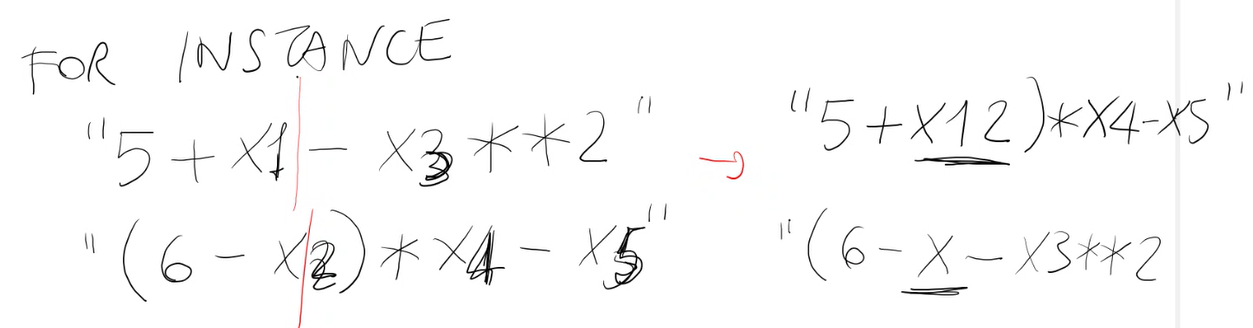
Questo perchè si ottengono figli sintatticamente non corretti.
Lo stesso problema si verifica con la mutazione.
L'idea è quella di cambiare rappresentazione per le istruzioni e per le espressioni.
La rappresentazione utilizzata è simile al linguaggio di programmazione Lisp (linguaggio più moderno -> closure). Tuttavia, è possibile anche utilizzare una rappresentazione diversa, come quella basata su alberi.
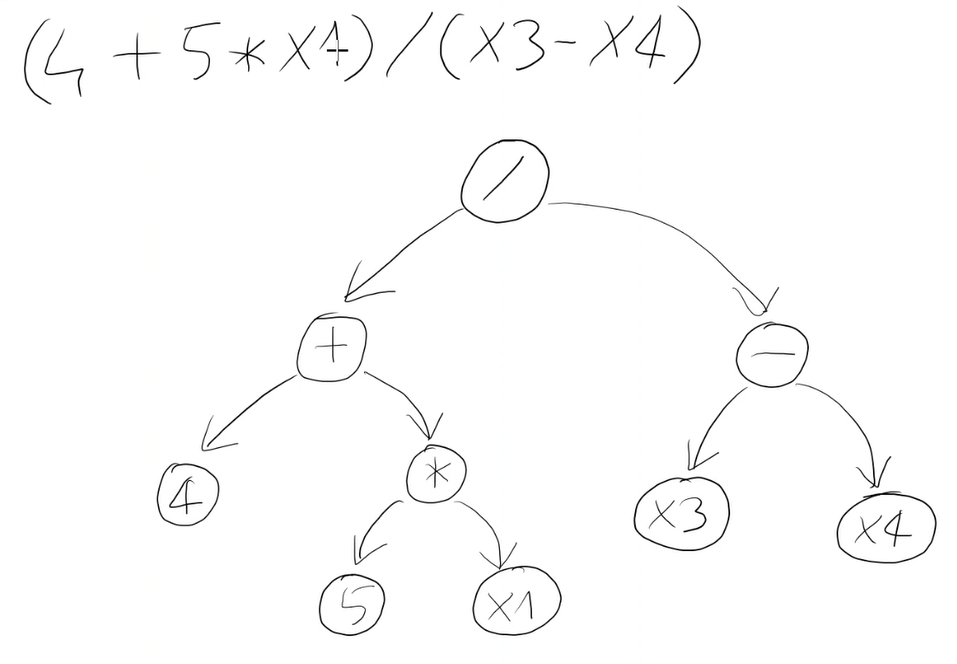
- Le foglie rappresentano:
- costanti
- variabili
- I nodi interni sono:
- operazioni (i figli sono gli argomenti dell'operazione --> operandi)
Per valutare un'espressione E rappresentata come un albero con i valori
V(n) = valore asssegnato al nodo n
if n is a leaf
if n is a constant
V(n) <-- n.costant
if n is a variable
V(n) <-- n[n.var_index]
else
V(n) <-- n.op(V(c1), ..., V(ck)) # dove c1, ..., ck sono i figli di n
Solitamente le operazioni hanno uno o due operandi. Tuttavia ci sono operazioni con più operandi, ad esempio l'operatore condizionale ha tre operandi (un nodo di un operatore condizionale ha tre figli)
initalize the population
create NP elements # devo avere un generatore di espressioni casuali
evaluate all the population elements
for g <-- 1 to max_gen
selection of the mating pool
crossover
mutation
evaluation
population update
end for
return the best individuals ever found
create NP tree
start with the root
with probability p it is a leaf (variabile o costante)
with probability 1-p it is an internal node -> scegli l'operazione e per ogni operando crea un sottoalbero
Alcune limitazioni possibili:
- massima profondità D
- se un nodo è ad una profondità D, è una foglia (lo si forza ad essere una foglia, altrimenti l'espressione risulta troppo complessa da trattare e/o l'albero è troppo complesso)
- esattamente profondità D
- se un nodo non è ad una profondità D, è considerato come un nodo interno
Per fare il crossover tra due alberi si sceglie un nodo del primo genitore
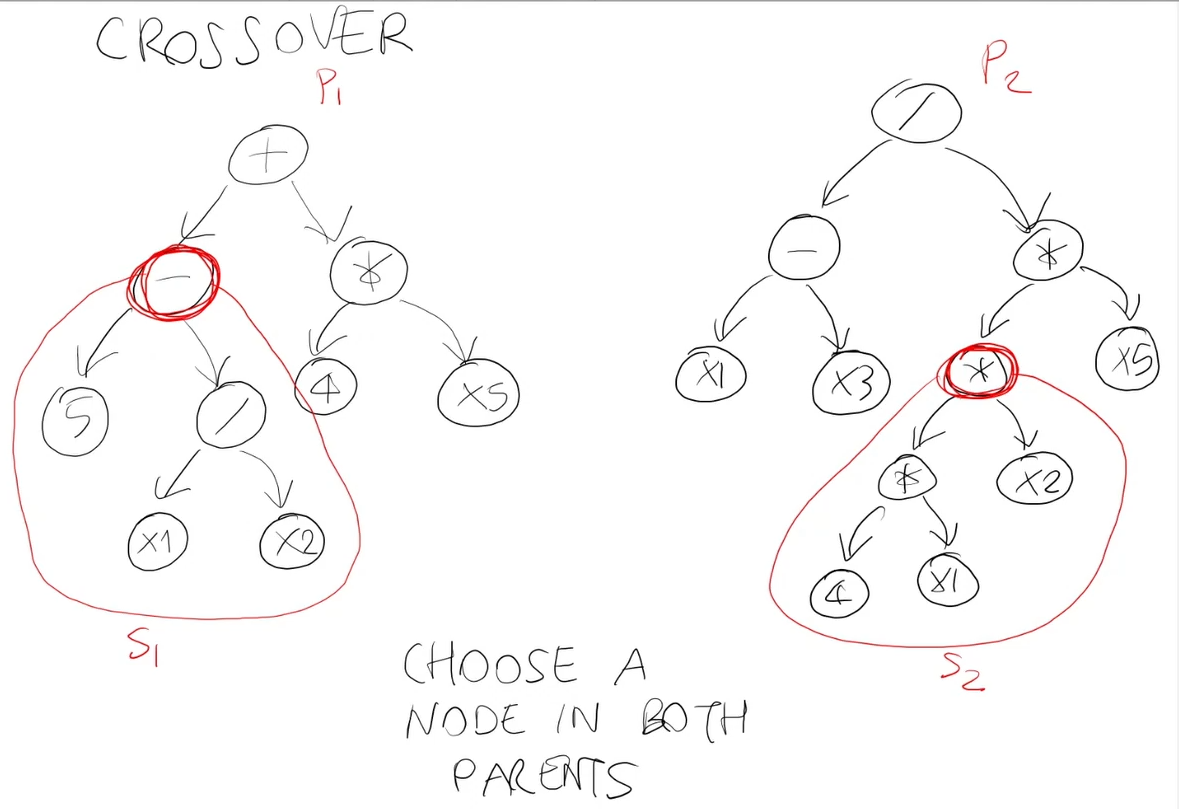
Per sceglierlo ci sono vari criteri (casualmente o dando più probabilità ai nodi foglia o ai nodi interni, a seconda della situazione in cui mi trovo, come ad esempio in base alla profondità).
I figli prodotti in questo modo sono espressioni sintatticamente corrette. Non importa come vengono selezionati i punti di scambio. Questo perchè io mi porto dietro l'intero sottoalbero (che produrrà un numero o un altro elemento, ma è comunque sintatticamente corretto).
Quello che cambia è che i figli possono avere un'altezza diversa rispetto ai genitori.
In generale, gli alberi possono avere altezze diversi (in un algoritmo genetico standard invece tendo ad avere elementi della stessa dimensione -> altrimenti non riuscirei a fare il crossover).
Durante l'evoluzione si tende a generare alberi sempre più alti perchè l'evoluzione tende a privilegiare individui sempre più alti. Questo fenomeno si chiama ploting e va combattuto perchè aumenta la complessità computazionale e temporale richiesta per valutare alberi troppo alti.
Bisogna quindi stare attenti ad alberi troppo alti:
- Si incorre in tempi computazionali maggiori per la valutazione e per le altre operazioni
- Gli alberi troppo grandi possono essere anche difficili da leggere.
Nonostante:
È importante notare che uno degli scopi della programmazione genetica è produrre espressioni leggibili (o almeno il più possibile leggibili). La programmazione genetica rientra nell'explainable artificial intelligence in quanto vengono prodotti risultati ed espressioni facilmente interpretabili dall'uomo (a differenza ad esempio di una rete neurale).
Inizialmente non veniva utilizzata nella GP e si utilizzava solo il crossover. Tuttavia, è un'operazione abbastanza semplice.
La mutazione di un albero consiste nello scegliere un nodo e sostituirne il sottoalbero che parte da tale nodo con un nuovo sottoalbero generato a caso. Per generare alberi o sottoalberi a caso è importante notare che le costanti numeriche corrispondono alle foglie, le operazioni corrispondono a nodi con due figli (radice quadrata avrà un nodo solo, un operatore generale può avere anche n figli). Concludiamo dicendo che è facile generare alberi a caso tramite una funzione ricorsiva. Si può anche fare in modo che l’altezza dell’albero sia limitata. Questo metodo può essere usato come meccanismo di inizializzazione.
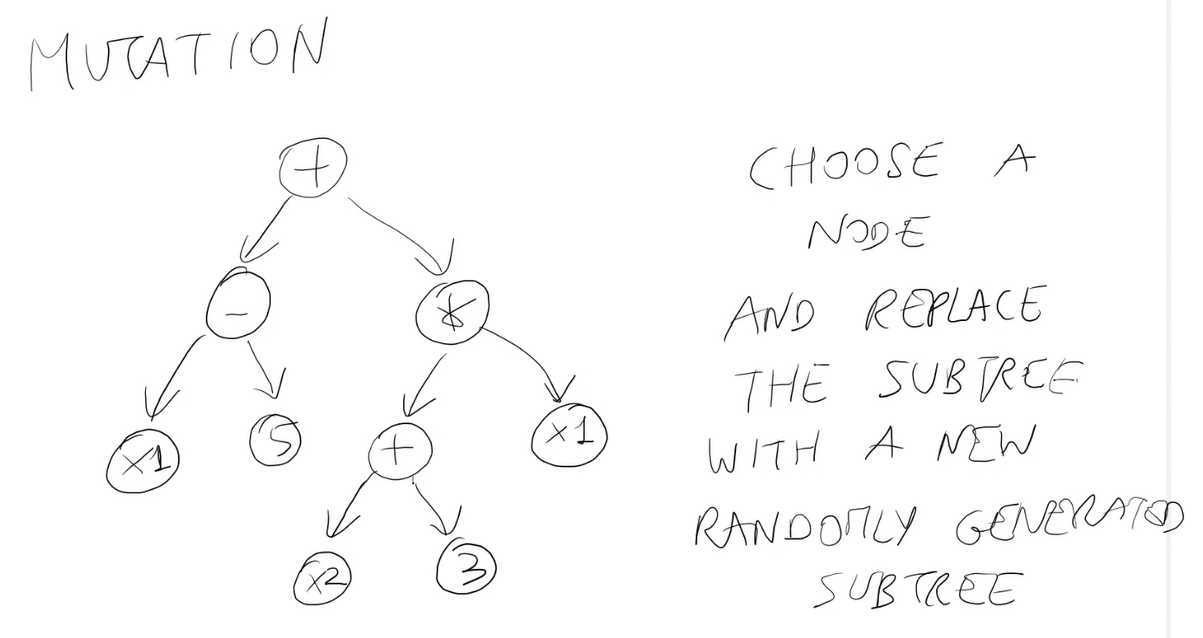
Più in alto è il nodo che scelgo e maggiore è l'effetto del cambiamento (perchè sto sostituendo una parte significativa dell'albero). Di conseguenza bisogna tenere in considerazione questo fattore per evitare un cambiamento eccessivo, si necessita quindi una calibratura sul cambiamento.
Calcolare la funzione di perdita (loss) L per ciascun individuo.
Più precisamente: Il meccanismo di calcolo della funzione di fitness L per un albero si svolge calcolando il valore della funzione per ogni esempio del dataset e poi calcolando la differenza tra il valore del risultato prodotto e il valore effettivo nell’esempio.
for j <-- 1 to NP
sum <-- 0
for i <-- 1 to N # N = numero di esempi
y <-- evaluate(g_j, x_i) # valuta g_j sull'esempio x_i -->
#g_j, funzione ricorsiva per valutare l'albero con gli input x_i
sum <-- sum + L(y, y_i) # y = valore trovato, y_i valore reale
end for
fobj[j] <-- sum
end for
Questo processo è molto pesante computazionalmente perchè devo farlo per ciascun individuo. Non è neanche facile parallelizzare il tutto anche perchè il codice di una g può essere molto diverso da quello di un'altra g.
La selezione del mating pool e l'aggiornamento della popolazione possono essere fatti come negli algoritmi genetici standard.
Con la programmazione genetica posso fare una forma particolare di Machine Learning, in cui tento di imparare non i pesi di una rete neurale, non i coefficienti di un modello lineare ecc, ma addirittura cerco di ricostruire la forma funzionale che mi permette di ottenere gli output a partire dagli input.
Con questo posso ad esempio creare circuiti, controllori, costruire policy per il reinforcement learning ecc..
Le limitazioni sono essenzialmente due:
- avere a disposizione il training set
- avere a disposizione delle risorse di calcolo non indifferenti (anche se nello svolgimento di alcuni compiti la programmazione genetica riesce ad essere competitiva rispetto alle reti neurali, ma tendenzialmente non lo è ma anzi richiede molta più computazione)

f viene rappresentata come un albero:
- gli operatori di crossover e mutazione sono definiti per gli alberi
-
Vantaggi
- È capace di apprendere un oggetto sintatticamente complesso (alberi, espressioni con operatori unari e binari, operazioni di assegnamento, iterarive, espressioni condizionali, porte logiche e circuiti ecc...).
-
Svantaggi
- La funzione obiettivo è computazionalmente difficile.
Questo perchè ogni elemento deve essere valutato per ogni esempio (ad esempio con una visita post-order) e ciò non può essere meccanizzato facilemente (a meno che non vengano utilizzati dei mini-batch come nel Machine Learning). - Non è facile migliorare la valutazione.
$T_1, ..., T_1$ --> alberi
$E_1, ..., E_n$ --> esempi
La valutazione viene fatta come una interoperazione.
Altrimenti l'alternativa sarebbe quella di utilizzare qualche forma di compilazione, ogni volta che viene generato un nuovo albero. Il tempo di compilazione ovviamente va preso in considerazione e quindi dal punto di vista computazionale potrebbe non dare vantaggi (non è quindi sempre conveniente utilizzare questa strategia).
- La funzione obiettivo è computazionalmente difficile.
Da un lato lo scopo della programmazione genetica è quello di addestrare, ottenere e sintetizzare espressioni e piccoli programmi. Inoltre la programmazione genetica ha l'obiettivo di produrre oggetti leggibili (non sempre). Due importanti caratteristiche sono quindi:
- espressività
- leggibilità
Dall'altro lato, la programmazione genetica è (molto) più pesante del machine learning:
- non c'è la backpropagation
- non si può parallelizzare per l'utilizzo su GPU (perchè tutti gli elementi usano codici diversi)
Ciò pone la GP in svantaggio rispetto al Machine Learning. Ci sono comunque stati dei tentativi per unire la GP al Machine Learning (Neural Network), la difficoltà per ottenere una modello simile è molto alta.
- Reti Neurali: presuppongono una rappresentazione puramente numerica del programma, è quindi stato necessario un gran lavoro -> Neural Tuning Machine (corrisponde ad un approccio ibrido) in cui è possibile utilizzare la BackPropagation.
Rappresenta i programmi come una sequenza di codici d'istruzione (istruction codes).
Ad esempio si possono rappresentare con delle sequenze di bytecodes, con il vantaggio di mantere crossover e mutazione come sequenze (più facile mantenerli). Lo svantaggio è che l'interprete deve essere limitato, altrimenti potrebbe andare in loop. Si può usare un limite di tempo: se entro un tot tempo l'interprete non ritorna un risultato la sequenza non è considerata valida. Inoltre è molto facile generare dei programmi senza senso.
Un altro svantaggio della gp lineare è che potrebbe produrre dei risultati che sono difficili da interpretare dagli umani (leggere il bytecode è difficile). Sarebbe necessaro avere un decompilatore.
Il vantaggio di questo approccio è che non è necessaria la ricorsione nè per generare nè per creare elementi. È possibile utilizzare solo cicli for per generare e valutare gli individui della popolazione. Inoltre anche la decodifica è totalmente numerica, per ogni individuo devo quindi conservare solo gli indici e l'operazione da fare, è quindi molto veloce rispetto alla classica gp basata sugli alberi.
Alcune forme di programmazione genetica (o altri algoritmi evolutivi) potrebbe essere utilizzate per migliorare (o correggere) dei programmi già esistenti (invece di crearli da zero). Questa forma si chiama genetic (o software) improvement.
La programmazione genetica tende a creare elementi con molte componenti:
- Questo causa un incremento notevole dei tempi di computazione.
- Inoltre gli elementi diventano difficile da capire e interpretare (sia per l'umano che a livello computazionale).
Per evitare il fenomeno di Bloat:
- Si limita la crescita, ad esempio penalizzando oggetti troppo grandi.
Funzione obiettivo di un oggetto e:
f_obj(e) = Loss(e) + k * Size(e) --> questo favorisce oggetti piccoli. - Utilizzare degli operatori che riducono gli oggetti (operatori sheink). Questi operatori prendono un oggetto e lo riducono.
- Semplificare gli oggetti. La semplificazione potrebbe essere computazionalmente pesante.
È un'area di ricerca che crea algoritmi di ottimizzazione prendendo ispirazione dalla natura (in particolare da grandi gruppi di animali).
Questo branca è particolarmente interessante perchè questi gruppi sono formati da individui con basse capacità di comunicazione e calcolo. Tuttavia l'intero gruppo è in grado di risolvere task molto più complessi rispetto al singolo individuo.
Ogni singolo individuo comporta poco sforzo nel lato di programmazione, tuttavia quando si combinano questi individui si riesce a risolvere problemi molto complicati.
Applicazioni dello Swarm Intelligence:
- Ottimizzazione
- Computer Grafica
- Robotica
In generale, nello Swarm Intelligence si ha una popolazione di individui (chiamati in realtà particelle o particles). Ogni individuo si muove nello spazio di ricerca e la funzione obiettivo è ottimizzata dall'intera popolazione (non dal singolo individuo in modo diretto).
I compiti che possono essere svolti dalla popolazione non sono semplicemente la somma dei comportamenti dei singoli individui, ma sono qualcosa di più complesso --> Emergenza
È un algoritmo che fa utilizzo della Swarm Intelligence, ed è pensato per l'ottimizzazione continua (è quindi un diretto rivale del Differential Evolution).
Il PSO è stato inventato a metà degli anni 90.
Si ha una funzione obiettivo che è definita per variabili reali. Queste variabili reali sono rappresentate come vettori di dimensione d.

Attrazione
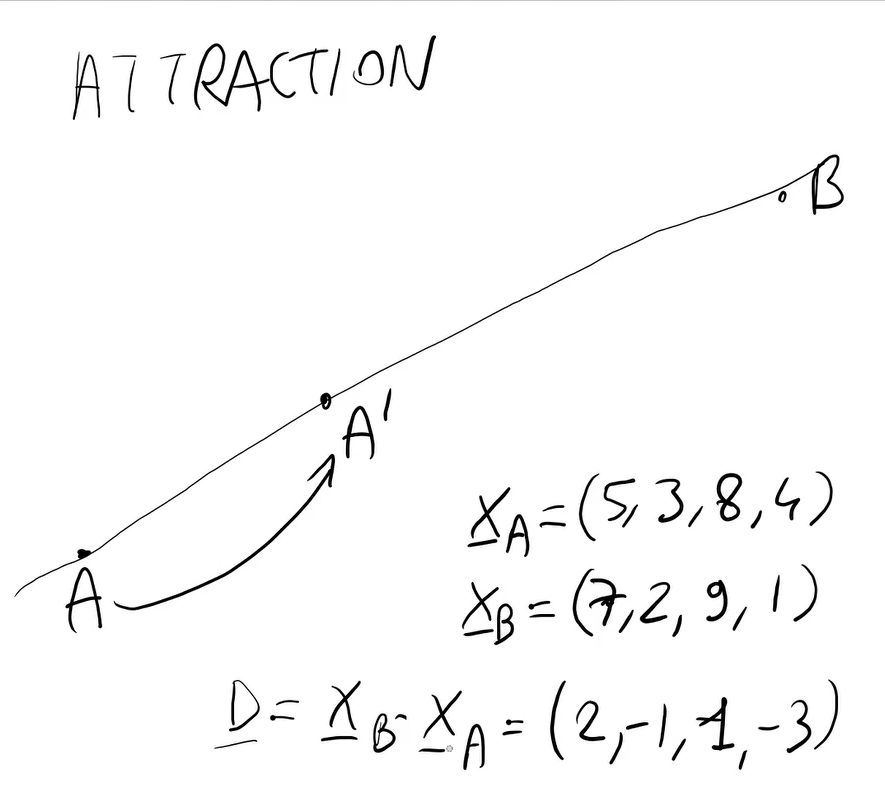
a' è ottenuto spostando A verso B
Questa tecnica è ad esempio utilizzata nei videogiochi. Si pensi alla situazione in cui un elemento nel videogioco deve inseguire un altro elemento nel videogioco che si sta muovendo. Per dire al primo elemento di inseguire il primo, non lo si può far muovere direttamente nella posizione dell'altro, ma si deve utilizzare questa tecnica.
Si ha una popolazione di N individui, in cui ciascun individuo ha le seguenti caratteristiche:
-
posizione corrente
$p^{(i)}$ (i sta per i-esimo individuo) -
velocità corrente
$v^{(i)}$ (si deve immaginare che questi individui si muovono ed hanno una velocità) -
memoria
$b^{(i)}$ (detto anche personal best) che corrisponde alla migliore posizione da lui trovata. Il migliore è inteso in termini della funzione obiettivo f.
Inoltre la popolazione ha anche una variabile globale
Global Best è il migliore dei Personal Best.
L'idea è di far muovere le particelle secondo due direzioni diverse (che si devono compensare l'una con l'altra). Da un lato la particella viene attratta dal suo personal best e dall'altro viene attratta dal global best. Queste due forze spingono la particella a cambiare velocità. Queste due forze danno l'idea del movimento di uno sciame perchè il global best fa puntare tutte le particelle verso la stessa direzione e il personal best fa puntare le particelle ognuna in una direzione diversa (tranne l'individuo migliore che ha il personal best uguale al global best). Questo fa esplorare lo spazio di ricerca.
Il comportamento del Particle Swarm è dato da due semplici equazioni.
Ciascun individuo aggiorna la sua posizione e la sua velocità con le seguenti regole:
-
nuova posizione
$p^{(i)}$ <--$p^{(i)}$ (posizione corrente) +$v^{(i)}$ (velocità corrente)
Nella fisica tradizionale la velocità$v_i$ è moltiplicata per Δt ma in questo caso lo valutiamo implicitamente uguale a 1
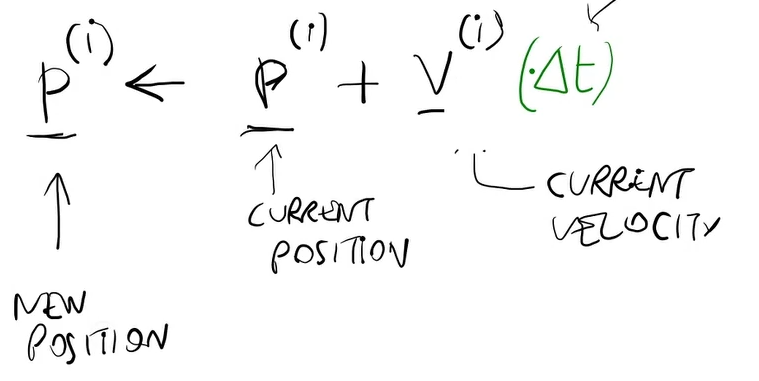
-
$v^{(i)} \leftarrow v^{(i)} + c_1 r_1$ ⊙$(b^{(i)} - p^{(i)}) + c_2 r_2$ ⊙$(g - p^{(i)})$ , dove:-
$c_1$ e$c_2$ sono due coefficienti -> parametri del PSO (solitamente sono fissati a 2.04) -
$v^{(i)}$ è la velocità corrente
-
$b^{(i)}$ è la miglior posizione trovata dalla particella
- g è la miglior posizione dell'intera popolazione
-
$r_1$ e$r_2$ sono due vettori casuali di dimensione d
- ⊙ è la moltiplicazione elemento per elemento (element-wise multiplication)
(1, 2, 3) ⊙ (0, 2, 5) --> (0, 4, 15)
-
Tuttavia in quanto si ha r1 ⊙ (bi - pi), si ha una distorsione della forza di attrazione in ogni dimensione.
Il coefficiente
N.B: Solo la particella che ha raggiunto g sa che è una buona posizione. Le altre non lo sanno. In un certo qual modo le altre si "fidano".
(g - pi) muove
Quando viene aggiornata la posizione ? E quando la velocità?
Ci sono due alternative possibili:
- La posizione viene aggiornata dopo la velocità.
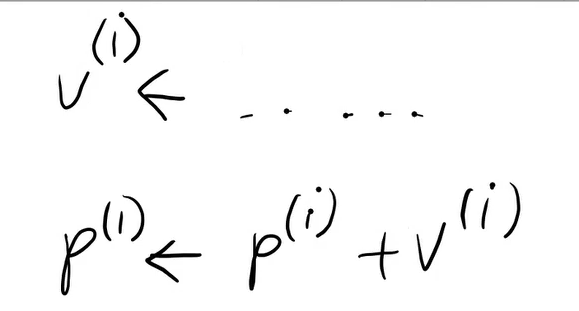
- Prima viene aggiornata la posizione poi viene aggiornata la velocità utilizzando la vecchia posizione.

Entrambi gli approcci funzionano.
g è invece aggiornata in modo similare
Inizializzazione della popolazione:
1. Scegliere posizione e velocità
2. bi = pi
g è il miglior bi
for gen <-- 1 ti max_gen
for i <-- 1 to N
update pi
update vi
update bi # evaluate f(pi)
end for
update g
end for
return g # g sarà il miglior elemento trovato da tutta la popolazione
Una rete di comunicazione tra le particelle (individui) può essere così rappresentata.
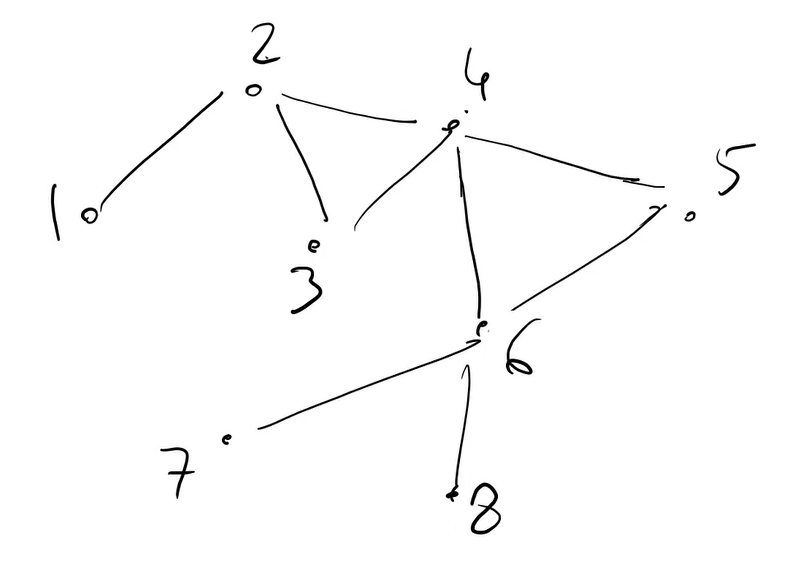
dove i numeri corrispondo alle particelle i. Inoltre va aggiunto il fatto che il grafo (Rete di comunicazione) è fisso, non dipende dalle posizioni (viene creato in maniera arbitraria).
Le particelle si scambiano delle informazioni -> si scambiano la miglior posizione che esse hanno trovato.
Non tutte le particelle sono in comunicazione diretta. Ciascuna particella può comunicare solo con quelle direttamente collegate.
Invece di utilizzare c2 r2 ⊙ (g - pi) la componente sociale è data da c2 r2 ⊙ (li - pi)
dove li è la migliore posizione (
g è la situazione in cui il grafo è completamente connesso (ogni particella comunica con tutte le altre, quindi li = g).
Non è sempre così, infatti in genere è frequente utilizzare dei grafi con una connettività bassa.
Un grafo che viene utilizzato spesso è il grafo ad anello:
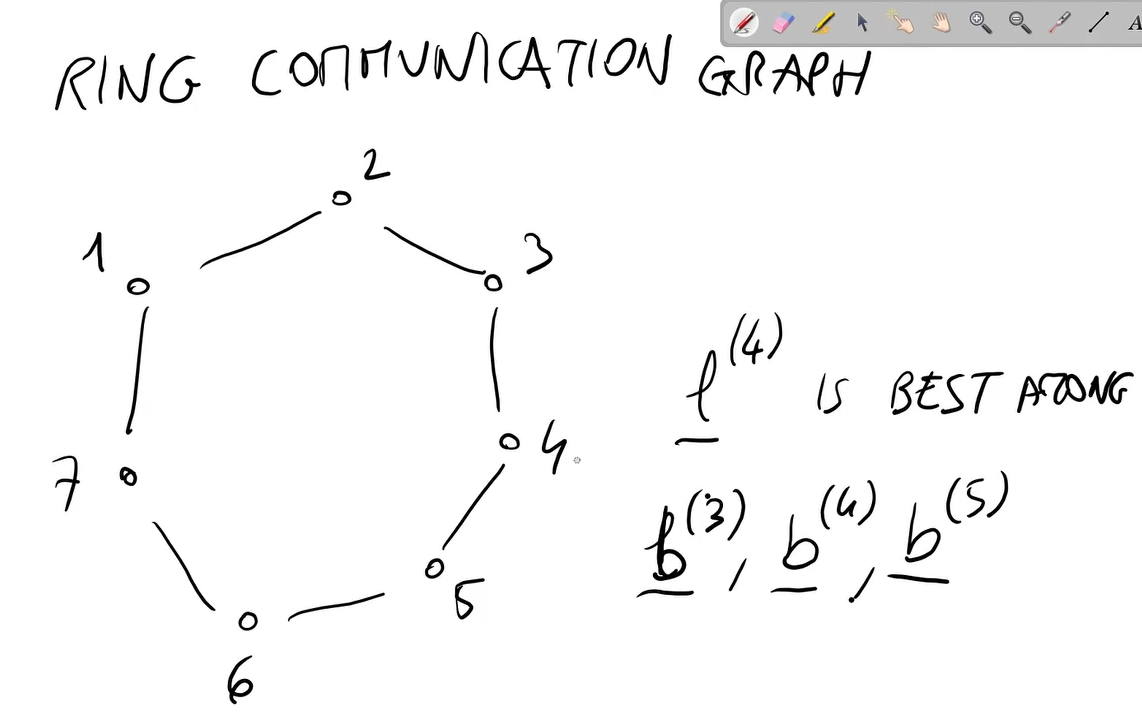
Questi grafi di comunicazione sono utilizzati per ridurre la possibilità di una convergenza troppo rapida. In sostanza si rallenta la convergenza.
La componente sociale è importante perchè senza di essa ogni particella andrebbe per conto suo e non ci sarebbe una convergenza. È come se ci fossero n esecuzioni indipendenti dello stesso codice, non ci sarebbe un concetto di popolazione.
La componente sociale da comunque l'idea di una popolazione -> di un obiettivo comune. Tuttavia pian piano si rischia che ogni personal best vada verso g e non si avrebbe ulteriore esplorazione. Si limita quindi la comunicazione per far continuare l'esplorazione più a lungo (non vanno tutte nella stessa direzione).
-
Componente di inerzia
Un terzo coefficiente è la componente d'inerzia
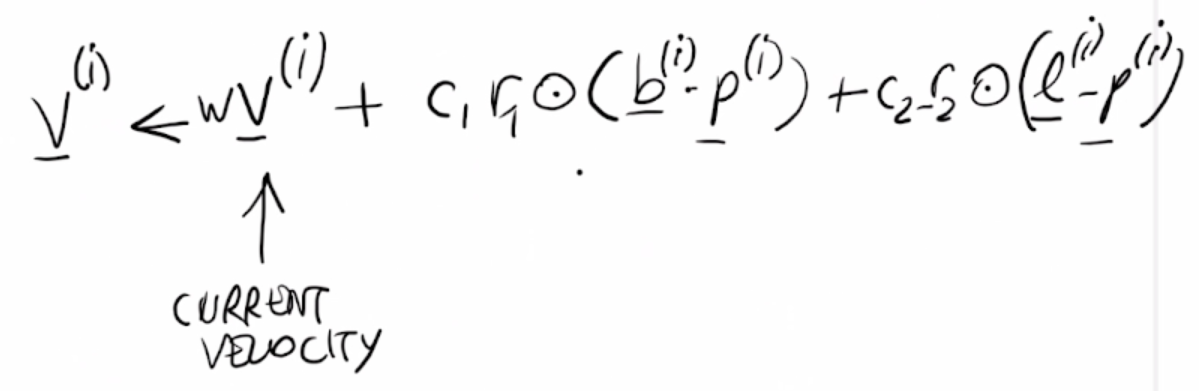
(dipende dalla velocità corrente). - È inoltre necessario utilizzare un limite per la velocità. Nel caso di una velocità troppo alta, la particella salta da un punto all'altro nello spazio in maniera esagerata e non si avrebbe una buona esplorazione.
Ad esempio si possono limitare tutte le componenti di$v^{(i)}$ nell'intervallo [-v_max, +v_max]. - Il PSO può essere implementato e utilizzato per problemi di ottimizzazione discreti.
La tecnica è simile a quella vista per il DE.
Ad esempio -> PSO binario:
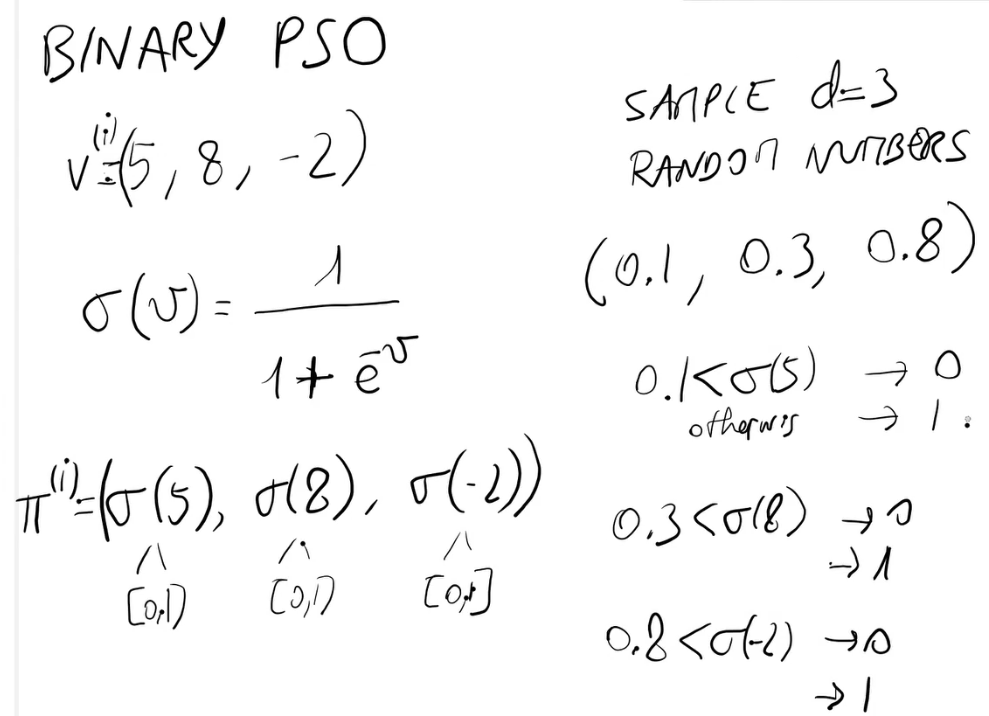
In questo modo si ha una stringa di 3 bit.
velocità --> stringa di bit
È uno dei migliori algoritmi di ottimizzazione basato su Swarm Intelligence. È ispirato al comportamento delle formiche.
Le formiche tendono a preferire percorsi più brevi. Per trovare il percorso più breve è sufficiente che le formiche tendano ad andare dove sono passate più spesso le altre formiche (seguire percorsi già battuti da altre formiche). Questo perchè in tali percorsi vi è una maggiore quantità di ferormone.
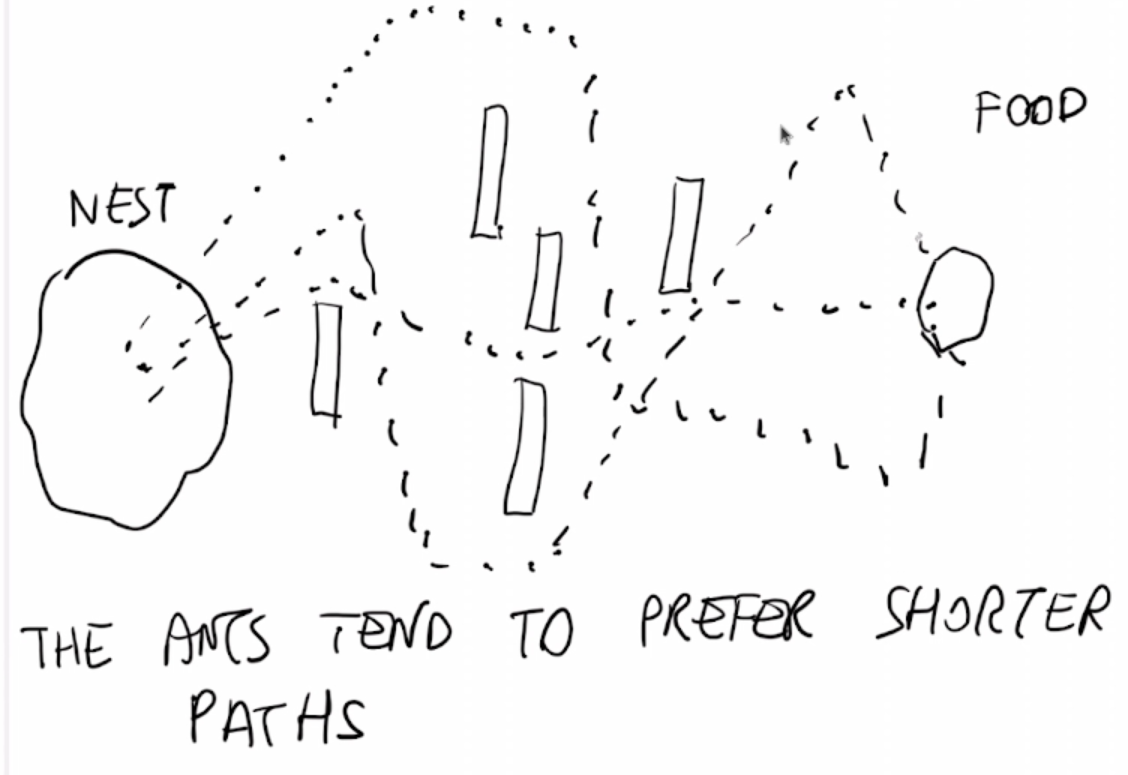
Tuttavia il feromone tende lentamente ad evaporare e quindi, se un percorso non è più seguito, sparisce.
L'idea è quella di simulare una colonia di formiche con lo scopo di risolvere problemi di ottimizzazione. In particolare per problemi di ottimizzazione combinatori su grafo (ottimizzazione discreta). --> Ant Colony Optimization
La naturale applicazione è quindi quella di risolvere problemi legati ai grafi.
Il grafo potrebbe essere costruito ogni volta che la formica arriva in un nuovo nodo.
Qui di seguito è mostrato come risolvere il TSP utilizzando ACO (Ant Colony Optimization)
Asimmetric TSP:
- n citta
-
$D_{ij}$ = distanza tra$c_i$ e$c_j$ -
Scopo: trovare il percorso cπ(1), cπ(2), ..., cπ(n), cπ(1) con il costo minore
- π è l'ordine di visita
- il percorso parte da una città, tocca tutte le città una sola volta e infine si deve tornare al punto di partenza.
Il costo di una soluzione è la somma di tutte le distanze percorse.
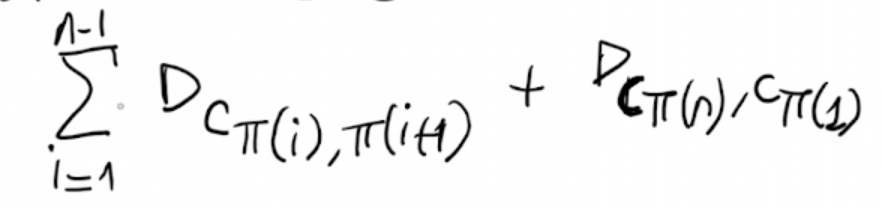
Il grafo su cui si muovono le formiche è cosi composto:
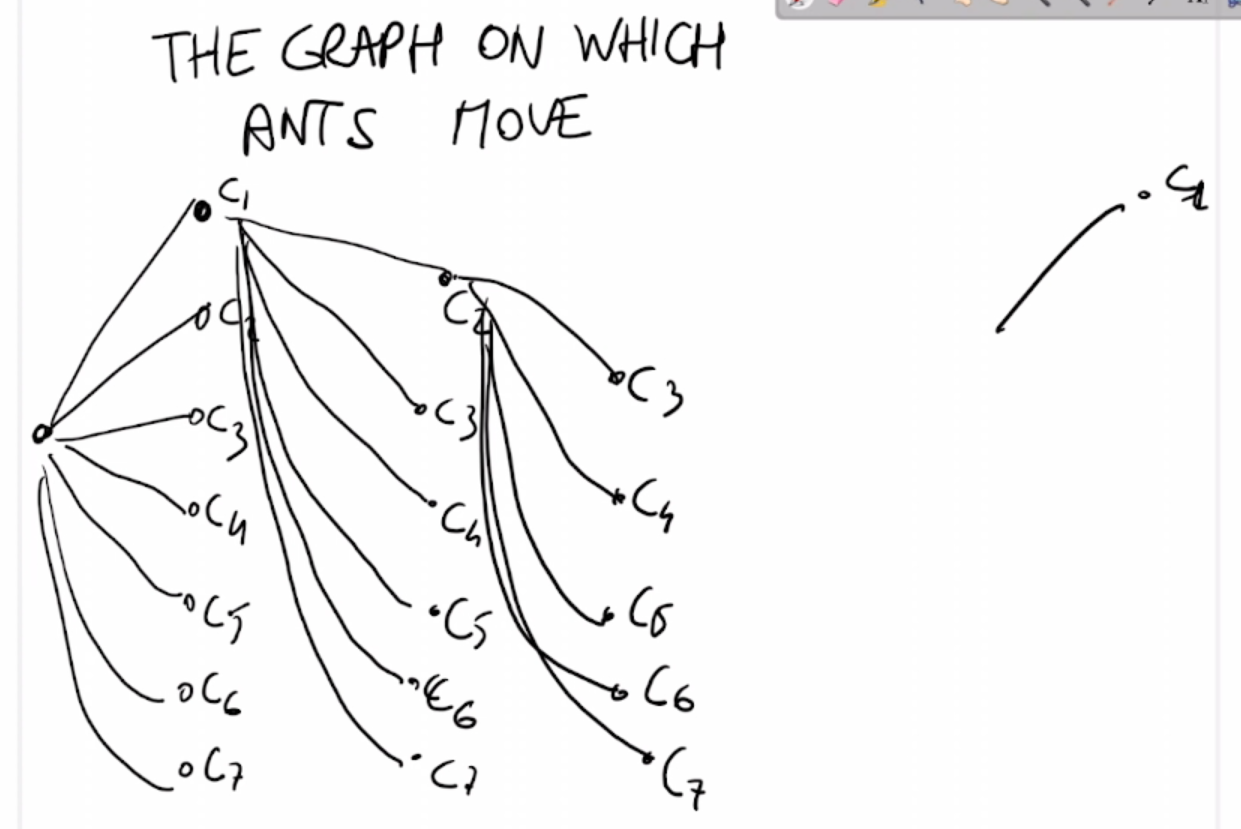
La sua dimensione è enorme, ragionare su questa rappresentazione è quindi molto difficile.
Il ragionamento da fare è quindi necessariamente diverso ed è descritto qui di seguito.
create_solution():
Una formica parte da un percorso vuoto π
while |π| < n
seleziona una città cj non appartenente al percorso π
aggiungi cj a π
end while
aggiungi cπ(1) a π
return π
Come fa la formica a scegliere un percorso?
La scelta della prossima città da visitare è una scelta probabilistica ed è influenzata da due valori:
-
Feromone
$\tau_{ij}$ ("tau") -
Funzione euristica
$\theta_{ij}$ ("teta")
dove i è la città corrente (ultima città visitata) e j è la città successiva.
- I valori di feromone sono memorizzati in una matrice che è gestita dalla colonia.
$\tau_{ij}$ rappresenta quanto la colonia ritiene buono andare da$c_i$ a$c_j$ (è un numero reale. In genere più è alto e più la colonia ritiene buono andare da$c_i$ a$c_j$ ).
- Il valore di euristica
$\theta_{ij}$ è un'informazione esterna che valuta la bontà della scelta$c_i$ ->$c_j$
Nel nostro caso$\theta_{ij}$ = 1/$D_{ij}$
in questo modo ciascuna formica tende (la scelta è probabilistica) ad andare alla città non visitata più vicina. -
Probabilistic Choice: La probabilità di scegliere j come città successiva del percorso è data dalla seguente formula:
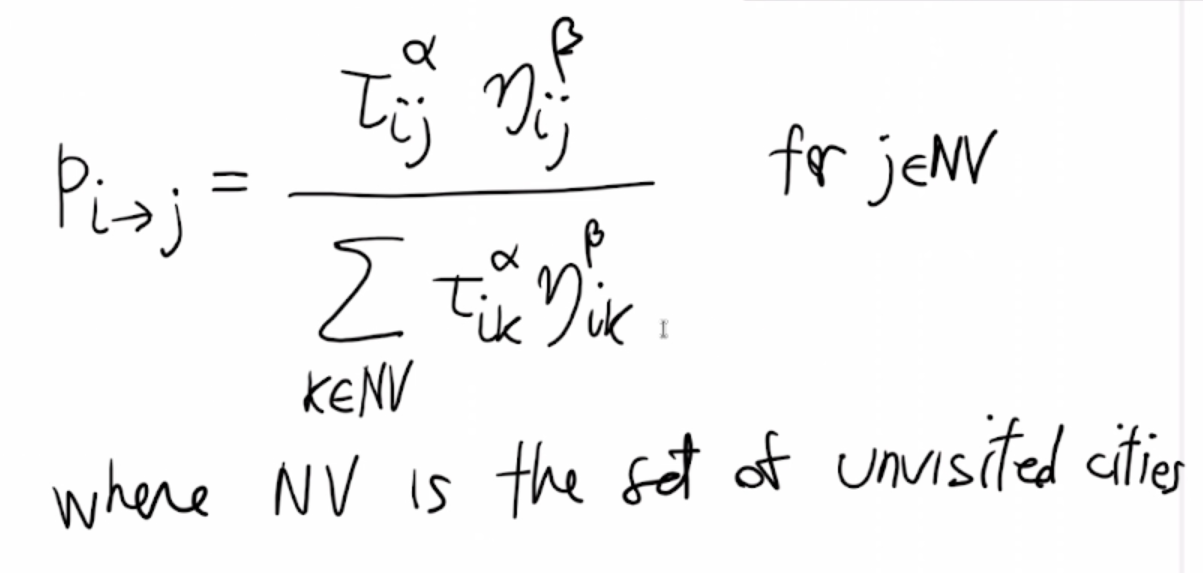
Per scegliere un numero basandosi sulle probabilità si fa utilizzo della roulette wheel.
Il valore probabilitico non esiste in natura ma viene aggiunto per migliorare le prestazioni.
La scelta della prossima città (in base al valore probabilistico) avviene in due passaggi:
- calcolare p(i->j) per tutte le città
$c_j$ non ancora visitate - selezionare
$c_j$ con il metodo della roulette wheel
Inizializzare la matrice dei feromoni τ
for g <-- 1 to max_gen
for i <-- 1 to num_ants
si <-- create_solution()
end for
eseguire l'evaporazione di τ
update_best_solutions
end for
return the best solution ever found
La fase di inizializzazione è abbastanza semplice:
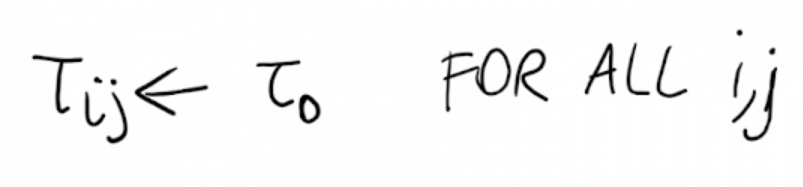
All'inizio mettendo tutti i valori uguali, le formiche scelgono solo in base all'euristica -> il feromone all'inizio non ha nessun contributo nella scelta delle formiche
create_solution():
Una formica parte da un percorso vuoto π
while |π| < n
seleziona una città cj non appartenente al percorso π
aggiungi cj a π
end while
aggiungi cπ(1) a π
return π
L'evaporazione è simulata nel seguente modo:
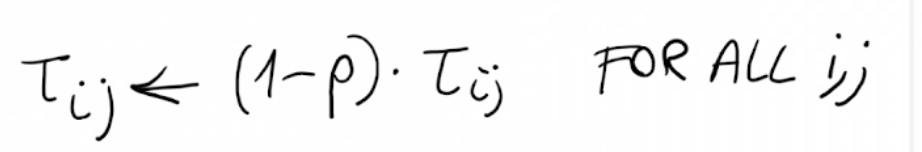
ῥ (rho) è un valore piccolo
Esempio: ῥ = 0.05 ; 1-ῥ = 0.95 ->
L'evaporazione è una sorta di decadimento esponenziale del feromone.
L'aggiornamento non esiste in natura.
Questo processo da una piccola reward (ricompensa) ad ogni coppia
Quali sono le buone soluzioni?
In natura se ne distinguono 2:
- Best_So_Far -> è la migliore soluzione di sempre s_bs (sarà anche il risultato finale restituito dall'algoritmo)
- Iteration_Best -> è la migliore soluzione trovata in questa generazione s_ib
rewards(s, k): # reward in base alla soluzione s
for all ci, cj che appaiono in s
τ_ij <-- τ_ij + K/Ls
Ls è il costo della soluzione s.
Ci sono 3 possibilità:
- reward(s_bs, w_bs)
- reward(s_ib, w_ib)
- reward(s_bs, w_bs)
reward(s_ib, w_ib)
w_bs e w_ib sono pesi che dipendono dal problema e devono essere calibrati. Ci sono anche varianti in cui non viene premiata una sola soluzione ma ad esempio anche la seconda migliore ecc...
- α -> indica quanto è importante τ nella scelta delle formiche
- β -> indica quanto è importante ϑ nella scelta delle formiche
- ῥ -> indica quanto velocemente evapora il feromone (influenza l'evaporazione: tanto più è alto, tanto più velocemente evapora il feromone)
- n_ants (numero di formiche) -> può influenzare la bontà dell'Iteretion_Best: più è alto il numero di formiche e più tentativi vengono fatti ad ogni iterazione. Facendo più tentativi è più probabile che vengano fuori soluzioni migliori ad ogni generazione (solitamente sta tra 20 e 50).
- w_ib -> indica quale soluzione viene premiata maggiormente: "premiare l'Iteration_Best significa premiare le novità" -> Exploration
- w_bs -> indica quale soluzione viene premiata maggiormente: "premiare il Best_So_Far significa spingere verso una convergenza" -> Exploitation
- max_gen
La matrice dei feromoni rappresenta la memoria collettiva della colonia.
La ricompensa non è della soluzione in sè, ma è data alle componenti della soluzione (archi/edges).
I valori euristici aiutano le formiche a scegliere, soprattuto all'inizio, perchè all'inizio il feromone non da contributo.
ACO risolve problemi discreti. ACO funziona creando, in modo incrementale, soluzioni di un problema combinatorio.
ACO viene ad esempio utilizzato per il TSP e per il VRP (Vehicle Routing Problem)
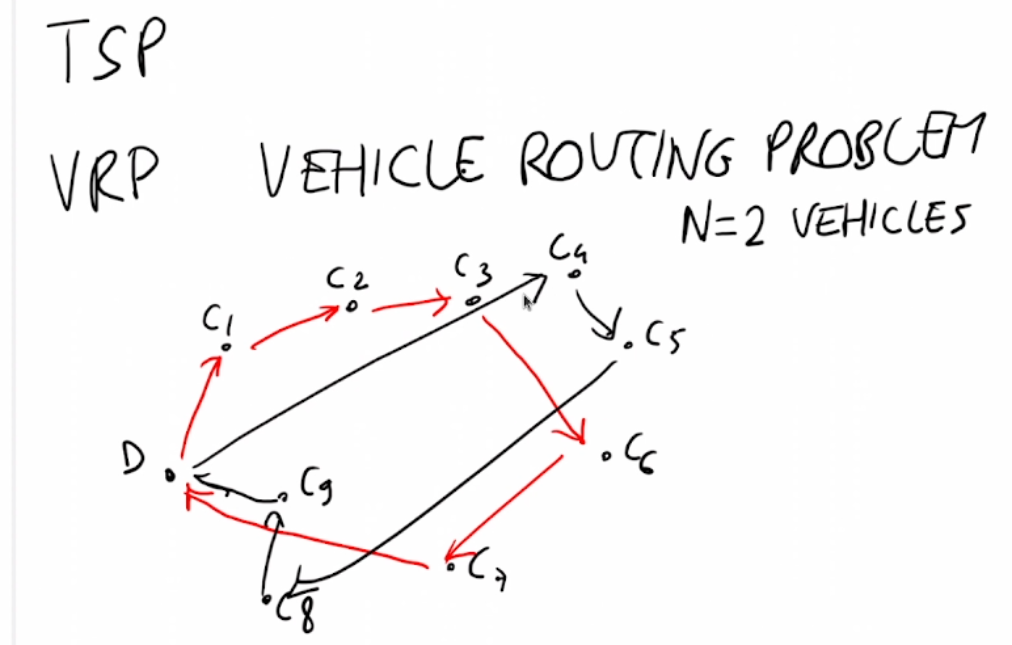
L'obiettivo è trovare n percorsi, in modo tale che la somma dei costi dei percorsi sia minimo.
Il VRP si riduce al TSP se si utilizza un solo veicolo.
ACO può essere utilizzato anche per risolvere problemi di scheduling e per problemi di assegnamento.
Problemi di assegnamento:

Problemi di Scheduling:
Si hanno n operazioni e si deve assegnare uno start_time a ciascuna operazione (possono anche essereci dei vincoli. Ad esempio: vincoli di precedenza tra le varie operazioni. Possono anche esserci dei vincoli di compatibilità: non possono esserci operazioni eseguite contemporaneamente tra loro.). La funzione obiettivo di un problema del genere è ad esempio quella di far terminare l'insieme di n operazioni nel minor tempo possibile.
Qui di seguito è riportato il codice per implementare una versione di ACO. Ovviamente è necessario riscrivere la classe per il problema del TSP, per qualsiasi informazione aggiuntiva vedere la relativa directory del particle_swarm tra le implementazioni degli algoritmi.
lass ACO_for_TSP:
def __init__(self,problem):
self.problem=problem
self.alpha=1
self.beta=1
self.rho=0.1
self.tau0=0.5
self.n_ants=20
self.w_ib=self.rho*2/3
self.w_bs=self.rho*1/3
self.n_cities=problem.get_dim()
def initialize(self):
self.phero=np.ones((self.n_cities+1,self.n_cities))*self.tau0
self.best_so_far=None
self.bs_cost=1e300 # very large value
self.sol=[None]*self.n_ants
self.sol_cost=np.zeros(self.n_ants)
def run(self,num_gen,seed=0):
if seed!=0:
np.random.seed(seed)
self.initialize()
for g in range(1,num_gen+1):
for n in range(0,self.n_ants):
self.sol[n]=self.generate_solution()
self.evaluate_solutions(g)
self.update_pheromone()
return self.best_so_far, self.bs_cost
def generate_solution(self):
sol=[]
rem=list(range(self.n_cities))
current=self.n_cities # a non existing city, it means that it must choose the first city to visit
for i in range(self.n_cities):
city=self.select_city(current,rem)
sol.append(city)
current=city
rem.remove(city)
return sol
def select_city(self,current,rem):
nr=len(rem)
prob=np.zeros(nr)
for i in range(0,nr):
city=rem[i]
tau=self.phero[current,city]
eta=1 if current==self.n_cities else 1/self.problem.dist_matrix[current,city]
p=tau**self.alpha * eta**self.beta
prob[i]=p
den=sum(prob)
prob=prob/den
# roulette wheel method
r=np.random.random()
i=0
while r>prob[i]:
r=r-prob[i]
i=i+1
return rem[i]
def evaporate(self):
self.phero=(1-self.rho)*self.phero
def evaluate_solutions(self,g):
for i in range(0,self.n_ants):
self.sol_cost[i]=self.problem.objective_function(self.sol[i])
self.ibest=self.sol_cost.argmin()
if self.sol_cost[self.ibest]<self.bs_cost:
self.bs_cost=self.sol_cost[self.ibest]
self.best_so_far=self.sol[self.ibest]
print("new best {} at gen. {}".format(self.bs_cost,g))
def update_pheromone(self):
self.evaporate()
#self.reward(self.best_so_far, self.w_bs/self.bbs_cost)
#self.reward(self.sol[self.ibest], self.w_ib/self.sol_cost[self.ibest])
self.reward(self.best_so_far, self.w_bs)
self.reward(self.sol[self.ibest],self.w_ib)
def reward(self,sol,delta):
current=self.n_cities
for i in range(self.n_cities):
city=sol[i]
self.phero[current,city] += delta
current=cityLo Swarm Intelligence è una tecnica ispirata al comportamente di gruppi di animali. Precedentemete abbiamo visto le seguenti tipologie (sono i più famosi):
- Particle Swarm Optimization -> pensato principalmente per problemi continui (non deve essere utilizzato necessariamente per problemi continui, può essere utilizzato anche per problemi discreti adattandolo)
- Ant Colony Optimization -> pensato principalmente per problemi discreti (allo stesso modo del PSO può comunque essere utilizzato per problemi continui ma è meno performante)
Ci sono altri algoritmi degni di essere citati. Qui di seguito verranno trattati.
-
È ispirato al comportamento delle api.
Divide gli individui del gruppo in due: - È ispirato al comportamento di un particolare tipo di uccelli. La metafora a cui si ispira è di un particolare tipo di uccelli che fa covare le sue uova in nidi di altri uccelli. Quello che succede è che i pulcini di questo uccelli prendono il sopravvento sull'altro nido.
- Ispirato al comportamento delle lucciole.
Esistono molti altri algoritmi di Swarm Intelligence. Sono più o meno tutti ispirati al comportamento animale ma non sono necessariamente tutti innovativi e/o performanti.
Qualsiasi algoritmo di ottimizzazione si scriva, esisterà comunque un problema per cui tale algoritmo funzionerà male.
Definizione Formale
Per qualsiasi algoritmo è sempre possibile trovare un problema in cui tale algoritmo produce risultati peggiori rispetto ad un altro algoritmo.
Non c'è quindi un modo semplice per affrontare i problemi di ottimizzazione.
Solitamente, gli algoritmi vengono confrontati tra loro.
Ad esempio per confrontare 2 algoritmi, l'idea è di utilizzare un benchmark con molte istanze di uno o più problemi e si fa successivamente girare ogni algoritmo su ogni singola istanza (questo passaggio viene ripetuto per più volte).
Successivamente si utilizzano dei test statistici sui risultati sperimentali, per determinare in modo scientifico quali sono i migliori algoritmi sui problemi di benchmark.
Il risultato di un test statistico è ad esempio: "L'algoritmo A1 è significativamente (al 95%) migliore di A2"
Ci sono inoltre delle competizioni internazionali in cui si devono implementare degli algoritmi per ottenere il miglior risultato su delle istanze di problemi dati.
Multi-Obiettivo significa che devo massimizzare (o minimizzare) più funzioni obiettivo e non solo una.
Ad esempio ho due funzioni obiettivo
$f_1(x^) <= f_1(x)$ e
Formulato in questo modo, il problema non sembra così difficile ma non è sempre risolvibile.
Io voglio trovare un punto che minimizza contemporanemanete due funzioni. Allora provo a trovare un valore che minimizza
Un esempio è il TSP, in cui le funzioni obiettivo sono il tempo e il consumo. In questa situazione io non riesco a minimizzare le due funzioni, in quanto sono in conflitto tra di loro, perchè ad esempio minimizzare il tempo potrebbe equivalere ad aumentare il consumo.
Date due soluzioni
.
.
.
e per almeno una o più j=1,...,k
S1 non domina S2 e S2 non domina S1.
In questo caso S1 e S2 non sono confrontabili.
Quando si opera con una sola funzione obiettivo, ci sono 3 possibilità:
- le due soluzioni sono uguali
- S1 è migliore di S2
- S2 è migliore di S1
Per quanto riguarda i problemi multi-obiettivo abbiamo una possibilità aggiuntiva alle 3 precedenti:
- le due soluzioni sono uguali
- S1 è migliore di S2
- S2 è migliore di S1
- S1 e S2 non sono confrontabili
I problemi multi-obiettivo richiedono di trovare un insieme di buone soluzioni che non sono comparabili tra loro.
Dall'insieme di soluzioni, posso poi scegliere in maniere autonoma la soluzione che preferisco secondo criteri personali.
Un insieme di soluzioni non comparabili è chiamato Pareto Front.
Nei problemi di ottimizzazione multi-obiettivo, il ruolo degli algoritmi evolutivi è molto importante, soprattutto gli algoritmi evolutivi basati sulle popolazioni, questo perchè io faccio evolvere una Pareto Front.
Uno degli algoritmi più famosi è il seguente:
È un algoritmo genetico basato su una tecnica che permette di velocizzare i calcoli della Pareto Front -> Non Dominated Sorting.
L'idea è di utilizzare un algoritmo genetico standard aggiungendo altre operazioni. In particolare questo algoritmo seleziona gli individui utilizzando due fattori:
- rank: indica quanto l'individuo è meglio rispetto agli altri
- distanza -> meccanismo che preserva la diversità: indica quanto l'individuo è distante rispetto agli altri
input: una popolazione di individui
output: ogni individuo p viene etichettato con un rank -> p.rank
for each p in P
Sp <-- []
np <-- 0
for each q in P
if p domina q then
Sp.append(q)
else if q domina p then
np <-- np+1
end for
if np == 0 then
p_rank <-- 1
F[1].append(p)
end for # finito questo for ho trovato tutti gli individui di rank = 1,
i <-- 1 # ora devo trovare gli altri
while F[i] != []
Q <-- []
for each p in F[i]
for each q in Sp
nq <-- nq - 1
if nq == 0 then
q_rank <-- i + 1
Q.append(q)
i <-- i + 1
F[i] <-- Q
end for
end for
end while
Questo viene utilizzato per aggiornare i valori dei rank, per quanto riguarda la distanza vedere qui di seguito.
Ordinando le soluzioni in ciascun
Il fattore distanza per
l = #p # numero di p
for each p in P
p.distance <-- 0
for j <-- 1 to k # k è il numero delle funzioni obiettivo
sort p rispetto a fj
p[0].distance <-- infinito
p[-1].distance <-- infinito
for i <--1 to l-2
p[i].distance <-- p[i].distance + ( p[i+1].fj - p[i-1].fj )/ (fj_max - fj_min)
Una volta che ho applicato il Non-Dominated sorting e la Crowding Distance, p è migliore di q se
p.rank < q.rank o (p.rank = q.rank AND p.distance > q.distance)
Seleziono tutti gli individui con rank più basso e poi mano a mano che mi servono più individui seleziono tutti i migliori individui con rank maggiore ma rispetto alla distanza.
In questo modo ho una popolazione ben diversificata (rispetto alla semplice Pareto Front in cui avrei solo quelli di rank 1 e potrei non poter migliorare più la mia popolazione).
Esistono in letteratura molte proposte di miglioramento per NSGA-II.
Queste proposte consistono nell'utilizzare il DE, il PSO e altre metaeuristiche e altri criteri per selezionare la popolazione.
Uno dei metodi alternativi per risolvere i problemi multi-obiettivo è quello di utilizzare la decomposizione. Quest'ultima è una tecnica che non usa la dominanza di Pareto.
L'idea è quella di avere una linearizzazione della funzione obiettivo: anzichè ragionare sulle singole funzioni obiettivo e cercare una soluzione che le minimizza tutte, la decomposizione crea una singola funzione obiettivo.
Sono possibili vari approcci:
-
Somma pesata (weighted sum)
- m funzioni obiettivo $f_1, ..., f_n$
- m pesi $ \lambda_1, ..., \lambda_n$ tali che
$x_i$ >= 0 ∀i = 1, ..., m e$\sum_{i=1}^{n}\lambda_i = 1$
I pesi devono essere maggiori uguali di 0 perchè ogni obiettivo deve contribuire in modo positivo (Altrimenti il contributo sarebbe l'opposto).
L'idea è di avere una funzione $g^{ws}(x|\lambda) = \sum_{i=1}^{n}\lambda_i f_i(x) $ con x che rappresenta la soluzione e$\lambda$ i pesi.
Un modo per risolvere il problema è quello di minimizzare$g^{gs}$ rispetto a x.
I$\lambda_i$ indicano il contributo relativo di$f_i$ .
A priori non esiste un vettore$\lambda$ che lavora meglio degli altri.
Gli algoritmi basati sulla decomposizione utilizzano una popolazione di "minimizzatori", ciascuno dei quali minimizza$g^{gs}(x | \lambda)$ , utilizzando il proprio vettore$\lambda$ . Ogni minimizzatore produce una soluzione$x^{(i)}$ . -
Un modo differente per aggregare le funzioni obiettivo
$f_i$ è il Tchebycheff's approaches.
Si valuta$z^{**} = (min f_1, min f_2, ..., min f_m)$ che in realtà non è un punto raggiungibile ma ci si può chiedere quanto è lontano.
$z = z(x) = (f_1(x), f_2(x), ..., f_m(x))$ ci chiediamo quanto è buono x a seconda di quanto è la distanza tra questo vettore e quello ideale.
La funzione di aggregazione sarà fatta in questo modo:
$g^{tc}(x | \lambda, z^) = max_{i =1, ..., m} {\lambda_i | f_i(x) - z^_i|}$ con $z^$ come punto di riferimento.
$z^ = (\mu_1, ..., \mu_m)$ dove$\mu_i$ è il valore minimo per$f_i$ fino all'iterazione corrente. Probabilmente anche questo punto non è raggiungibile.
Il termine a destra della formula per$g^{ts}$ è una specie di distanza tra il vettore$z(x)$ e il vettore di riferimento$z^*$ .
Anche qui si ha una popolazione di minimizzatori, ciscuno dei quali utilizza dei valori diversi per$\lambda^{(i)}$ .
Entrambe le funzioni di aggregazione hanno la seguente proprietà:
utilizzando
- Si ha una popolazione di n individui
- ogni individuo ha:
- un vettore
$\lambda^{(i)}$ - una soluzione iniziale
$x^{(i)}$ - un vettore
$F^{(i)} = (f_1(x^{(i)}), ..., f_n(x^{(i)}))$
- un vettore
Per 2 funzioni obiettivo, la scelta dei

for each individual
let B(i) be the of T "neighbors" of i, that is the set of T individuals whose lambda is closer to lambda(i)
Ad esempio per T = 2
B(i) = {i-1, i+1}
$d(\lambda^{(i)}, \lambda^{(i+1)}) = \sqrt{0.1^2 + 0.1^2} = \sqrt{0.02} $
Tutte la altre
ep <- [] #(external population. Questa variabile servirà per conservare gli individui migliori che sono stati creati durante l'esecuzione dell'algoritmo. Vorremmo mantenere in ep le soluzioni che non sono dominate da altre.)
generate the initial values for x^(i), lambda^(i), F^(i)
initialize z^*
for g <- 1 to num_gen
for i <- 1 to N
select k,l in B(i) (k != l)
generate y^(i) from x^(k) and x^(l) #utilizzando ad esempio qualche forma di crossover o altri operatori binari
update x^* by considering f_j(y^(i))
for each h appartente a B(i)
if g(y^(i) | lambda^(h), z^*) < g(x^(h) | lambda^(h), z^*)
x^(h) <- y^(i)
F^(h) <- (f_1(y^i), ..., f_m(y^(i)))
end if
end for
remove all the elements of EP which dominated by y^(i)
add y^(i) if it is not dominal
end for
end for
return ep
Ci sono molti modi per generare
Un problema facile da rendere multi-obiettivo è il knapsack:
Trovare un vettore binario x tale che
Ad esempio:
-
$f_1(x)$ = valore in euro -
$f_2(x)$ = utilità
Con
-
$w_{i1}$ = peso dell'oggetto i -
$w_{i2}$ = volume dell'oggetto i
Un altro problema multi-obiettivo interessante è quello dello scheduling.
- n jobs
$j_1, ..., j_n$ - m macchine
$M_1, ..., M_m$
Ogni job
-
$o_{i1}$ deve essere eseguito da$M_1$ -
$o_{im}$ deve essere eseguito da$M_m$
Ogni operazione
Inoltre le operazioni di ogni job devono essere eseguite in questo ordine:
Ciascuna macchina ad ogni momento può eseguire al più un'operazione
Il problema del Flow-Shop è quello di trovare una schedulazione per tutte le operazioni.
Ad esempio:
trovare tutti i
dove s è lo start time e p il tempo di processamento.
L'obiettivo è quindi minimizzare
Possibili funzioni obiettivo:
-
Total flow-time =
$\sum_{i=1}^{n} c_j$ -
Tardiness =$\sum_{i=1}^{n} max(c_i - d_i, 0)$ con
$d_i$ = istante in cui il job dovrebbe completarsi.
Lo scheduling multi-obiettivo consiste nel trovare uno schedule che minimizza alcune funzioni obiettivo.
I problemi di scheduling hanno molte applicazioni industriali.
Inoltre anche il TSP può avere formulazioni multi-obiettivo considerando tempo e consumo.
Il decision maker può scegliere una qualsiasi soluzione tra quelle prodotte dal nostro ottimizzatore multi-obiettivo (perchè non essendoci tra queste relazioni di dominanza, possono essere viste come equivalenti) utilizzando un altro criterio.
Ragionamento in termini di incertezza -> l'incertezza può essere introdotta in termini:
- qualitativi ("È probabile che domani ci sia brutto tempo", "È improbabile che Napoleone sia stato avvelenato")
- quantitativi ("La probabilità che domani piova è 0.6" -> P(R) = 0.6)
Esistono altre forme per rappresentare l'incertezza:
- belief functions
- possibility
- qualitative probability
- ma la più utilizzata è la probabilità
Il problema delle probabilità è il costo computazionale (lavorare con le probabilità porta spesso a dover risolvere problemi computazionalmente difficili) ma ci sono molte tecniche per ridurre tale costo.
P(x) = probabilità che la proposizione x è vera
Leggi del calcolo delle probabilità:
- 0 <= P(x) <= 1 per tutte le proposizioni
- P(not x) = 1 - P(x)
- P(x OR y) = P(x) + P(y) se x AND y è impossibile (se è una contraddizione)
Esempio 1
Lancio di due dadi:
-
$E_1$ : il risultato del primo dado è > 4 ---> ($\dfrac{2}{6}$ ) -
$E_2$ : il risultato del secondo dado è > 4 ---> ($\dfrac{2}{6}$ ) - P(
$E_1$ AND$E_2$ ) = ?
Se x è indipendente da y allora P(
- P(x | y) con x e y proposizioni ---> è la probabilità che x sia vero sapendo che y è vero (si considerano le sole situazioni in cui y è vero)
Esempio 2
Lancio di un dado:
- P(il risultato è >= 3 | il risultato è dispari)
P(x | y) =
Notare che P(y) può essere 0 ma questo non significa che y sia impossibile (ad esempio una contraddizione.)
x è indipendente da y se P(x | y) = P(x), ovvero conoscere che y è vero non influisce sulla probabilità di y.
In generale: P(x AND y) = P(x | y) * P(y)
(se x è indipendente da y: P(x AND y) = P(x) * P(y))
Supponiamo di avere n proposizioni elementari
Con una proposozione posso creare
Per ragionare su
Dato che
Da
È importante sapere che senza la relazione di indipendenza,
Esempio
Nel caso in cui ogni proposizione è indipendente da tutte le altre
Questo significa che:
-
se non c'è indipendenza tra le n proposizioni elementari, sono necessari
$2^n$ valori di probabilità per calcolare P(z) ->$O(2^n)$ - quando tutte le proposizioni sono indipendenti tra loro, sono necessarie le sole probabilita
$x_i$ ->$O(n)$
Conoscere solo $E_2$ o conoscere $E_1$ e $E_2$ influisce sulla probabilità di $E_3$ ?
No, sapere anche
Questo concetto è chiamato:
P(x) = P(x | y) ----> indipendence
P(x|y) = P(x| y, z) ----> conditional indipendence
x ⫫ z | y ----> x è indipendente da z dato y
Nell'esempio della staffetta:
$E_1$ $E_2$ $E_3$ $P(E_3 | E_1, E_2) = P(E_3 | E_2)$
=
-
Situazione di NO conditional indipendence:
$P(E_1)$ $P(E_2 | E_1)$ $P(E_2 | NOT E_1)$ $P(E_3 | E_1, E_2)$ $P(E_3 | NOT E_1, E_2)$ $P(E_3 | E_1, NOT E_2)$ -
$P(E_3 | NOT E_1, NOT E_2)$
Servono quindi 7 valori in totale.
-
Situazione di conditional indipendence:
$P(E_1)$ $P(E_2 | E_1)$ $P(E_2 | NOT E_1)$ $P(E_3 | E_2)$ -
$P(E_3 | NOT E_2)$
Servono quindi 5 valori in totale.
In generale:
n proposizioni elementari
È veramente importante trovare il maggior numero di relazioni di indipendenza condizionta. È necessario individuare per ogni variabile, quali sono le variabili a cui essa è strettamente collegata.
Sono un modello probabilistico definito tramite un grafo.
È usato per rappresentare in modo compatto un modello probabilistico.
Invece di avere semplici proposizioni, le quali possono essere vere o false, possiamo parlare di variabili discrete. Ogni variabile può avere un dominio finito (un numero di valori possibili per tale variabile).
n variabili
Le proposizioni possono essere viste come variabili binarie (con
Esempio
Nel caso di un dado perfettamente bilanciato
Un'altra situazione che potrebbe verificarsi è
lo è anche
In generale, è possibile calcolare la probabilità che alcune variabili abbiano determinati valori.
È possibile estendere il concetto di indipendenza e indipendenza condizionata al caso di variabili discrete.
Una Rete Bayesiana è composta da
- un insieme di n variabili discrete (casuali)
$x_1, ..., x_n$ con il dominio finito$D_1, ..., D_N$ - un grafo aciclico diretto i cui nodi sono le variabili e gli archi rappresentano una diretta influnza di una variabile rispetto ad un'altra
- per ciascuna variabile
$x_i$ si ha una tabella che specifica$Pa(x_i = a | Pa(x_i)=b)$ per ogni a appartente a$D_i$ a per tutte le combinazioni b di valori dei genitori di$x_i$
Gli altri valori possono essere calcolati come segue:
Questo modello ha 8 parametri (in realtà ne avrebbe 16, ma gli altri possono essere ricavati a partire da questi 8) (Vedi dopo come calcolare il numero di parametri).
Esempio
-
$x_1$ : piove -
$x_2$ : impianto irrigazione acceso -
$x_3$ : terreno fangoso -
$x_4$ : scarpe sporche -
$x_4$ ⫫$x_1$ |$x_3$
Il fatto che ha piovuto non mi interessa, il terreno è fangoso e questo spiega le scarpe sporche.
È l'assenza di archi che ci dice che c'è indipendenza in modo condizionato, non la presenza di archi.
È importante che il grafo sia diretto e aciclico perchè:
- diretto -> gli archi hanno una direzione, dalla casua all'effetto
- aciclico -> non ci sono loop (altrimenti significa che una variabile causa se stessa)
-
Selezionare un ordine nelle variabili rispetto agli archi -> Se
$x_i$ -->$x_j$ allora$x_i$ precede$x_j$ (ordine topologico)
Per ogni variabile
per ogni variabile
Nell'esempio in figura Pa(
-
$x_4$ è indipendente da$x_1$ |$x_3$ -
$x_4$ è indipendente da$x_2$ |$x_3$
In generale il modello ha
Nel caso in cui tutte le variabili sono binarie
In pratica Pa(
-
inferenza -> calcolare il valore di una variabile, conoscendo il valore di altre variabili --->
$P(x_A = a | x_B = b)$ = ? con A, B indici (insiemi disgiunti) e a e b combinazioni di valori. - learning (apprendimento) -> possono apprendere la parte numerica o l'intera rete dai dati.
Le Reti Bayesiane sono uno strumento importante per ragionare sotto l'incertezza utilizzando la probabilità. Quest'ultime rappresentano modelli in un modo compatto (numero ridotto di parametri) e quindi riducono il costo computazionale.
Esempio di inferenza (sulla tabella precente)
Per trovare gli altri termini si procede come di seguito (per convenienza se ne calcola solo una ma il procedimento è lo stesso per tutte):
Da queste formule è possibile calcolare il risultato.
Ci sono degli algoritmi per calcolare
-
Variable Elimination (chiamato anche Metodo Esatto) ---> è una tecnica che consente di calcolare la probabilità di un determinato insieme di variabili
$P(x_C = c)$ per tutti gli c.
Esempio:$P(X_1 = x_1 AND X_4 = x_4)$
$P(X_1, X_4) = \sum_{X_2 X_3} P(X_1, X_2, X_3, X_4)$ =$\sum_{X_2 X_3} P(X_1) P(X_2) P(X_3 | X_1, X_2) P(X_3 | X_4)$ =
=$P(X_1) \sum_{X_2} P(X_2) \sum_{X_3} P(X_4 | X_3) P(X_3 | X_1, X_2)$ -
Sampling
$P(x_C = c)$ --> estrai N campioni da$X_C$ e conta quanti valori hanno il valore c. Questa è una stima di P (non è un valore esatto).
Svantaggi del Metodo Esatto (Variable Elimination):
- Costi computazionali elevati
Svantaggi del Sampling:
- N deve essere grande abbastanza da permettere una buona precisione.
- In caso di eventi rari, la stima potrebbe essere 0 (non è un valore corretto, la probabilità è bassa ma non 0)
- Markov Networks -> non usano DAG ma utilizzando dei Grafi non Orientati.
Venivano utilizzati per rappresentare e ricostruire le immagini (image processing). - Hidden Markov Models -> ci sono delle variabili nascoste e delle variabili visibili.
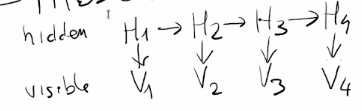
Le variabili nascoste sono influenzate tra di loro.
Utilizzato nel riconoscimento del parlato (speech recognition). - Naive Bayes ---> utilizzato ad esempio per la classificazione
!
Le reti Bayesiane sono costituite da un DAG i cui:
- nodi: sono variabili casuali discrete
-
tabelle di probabilità: per ogni nodo
$v_i$ è la distribuzione di probabilità condizioanta su tutti i valori dei genitori
- visit to asia: 1 parametro (probabilità di essere vero)
- smoking: 1 parametro (probabilità di essere vero)
- tubercolosi: 2 parametri ->
- P(T=1 | A=0)
- P(T=1 | A=1)
- cancro ai polmoni: 2 parametri ->
- P(L=1 | S=0)
- P(L=1 | S=1)
- dispnoea: 4 parametri ->
- P(D=1 | L=0, B=0)
- P(D=1 | L=1, B=0)
- P(D=1 | L=0, B=1)
- P(D=1 | L=1, B=1)
Inferenza
P(T=1 | A=1, S=1, X=0, D=1) = ?
Il primo parametro è la diagnosi e il secondo è l'evidenza
scegli un ordine delle variabili X_1, ..., X_n
per ciascuna variabile X_i #secondo l'ordine
trovare tutte le tabelle dove appare X_i
moltiplicare le tabelle trovate, ottenendo un'unica tabella T
eliminare X_i da T ottenendo T'
sostituisci le tabelle usate con T'
Il costo computazionale dell'eliminazione delle variabili dipende dalla forma del grafo, in particolare se è simile ad un albero oppure no. Questa proprietà è chiamata tree-width. Se ogni nodo ha al più k genitori, il costo computazionale è
È disponibile un'implementazione relativa alle Reti Bayesiane e al calcolo delle inferenze nell'apposita directory del codice. Viene utilizzata la libreria pgmpy.
Una Rete Bayesiana può produrre risultati interpretabili perchè tutto si basa sulle teorie delle probabilità. Tuttavia una rete Bayesiana richiede una grande potenza computazionale per eseguire le inferenze e l'apprendimento.
Non è particolarmente difficile quando il grafo è noto.
Per allenare una Rete Bayesiana è necessario un dataset e la funzione di 'loss' (rifacimento alle Neural Network) e la verosimiglianza -> trovare la rete che attribuisce ai campioni del dataset la maggior probabilità possiile.
Lo scopo del learning è trovare la Rete Bayesiana che da agli esempi del training set la maggiore probabilità possibile.
- Se il grafo è noto allora le tabelle della rete sono quelle che si ottengono contando e dividendo per il numero degli esempi.
- Se il grafo non è noto, il problema è molto più difficile e viene risolto utilizzando alcune strategie, come le seguenti:
- utilizzare test statistici per scoprire le relazioni di indipendenza condizionata
- approccio di ricerca --> corrisponde ad un problema di ottimizzazione (ho un insieme di possibili grafi e devo scegliere quello che da' al training set il punteggio più alto)
- approccio basato sui vincoli -> costruisce la rete Bayesiana con dei meccanismi di tipo costruttivo (prendono il training set e cercano di costruire i possibili archi). L'approccio più famoso è MMHC
Le Reti Bayesiane possono essere estese in molti modi:
- dinamico, ad esempio si hanno più variabili che variano nel tempo
- Reti Bayesiane relazionali
- Reti Bayesiane nel continuo (con variabili gaussiane)
Si occupa di vaghezza, che è diversa dall'incertezza.
Esempio: "oggi è bel tempo".
Questa informazione è vera o falsa? Potrebbe non essere nè vera nè falsa.
Esempio: "Una persona di 35 anni è giovane".
Questa informazione è vera o falsa? Potrebbe non essere nè vera nè falsa. Non c'è una soglia specifica secondo cui una persona è giovane o vecchia.
La logica fuzzy da' ad una proposizione un valore di verità intermedio in [0, 1].
Ad esempio:
- 0 -> Falso
- 0.5 -> via di mezzo
- 0.9 -> quasi vero
- 1 -> Vero
V("lunedì il tempo era bello") = 0.1
La logica Fuzzy è stata inventata da un ingegnere nel 1965 (L. Zadeh).
Un insieme Fuzzy è una collezione di elementi con un grado di appartenenza all'insieme.
Un insieme normale ha un insieme di appartenenza in {0, 1} a differenza degli insiemi Fuzzy.
È possibile calcolare l'unione, l'intersezione, il complementare e il prodotto cartesiano di insiemi Fuzzy.
Esempio: complementare di un insieme delle persone non giovani.

Il complementare si ottiene con il complemento a 1.
- unione -> massimo
- intersezione e prodotto cartesiano -> minimimo
Servono ad indicare delle frasi che parlano di quantità.
Esempio: "la temperatura è alta ma non troppo"
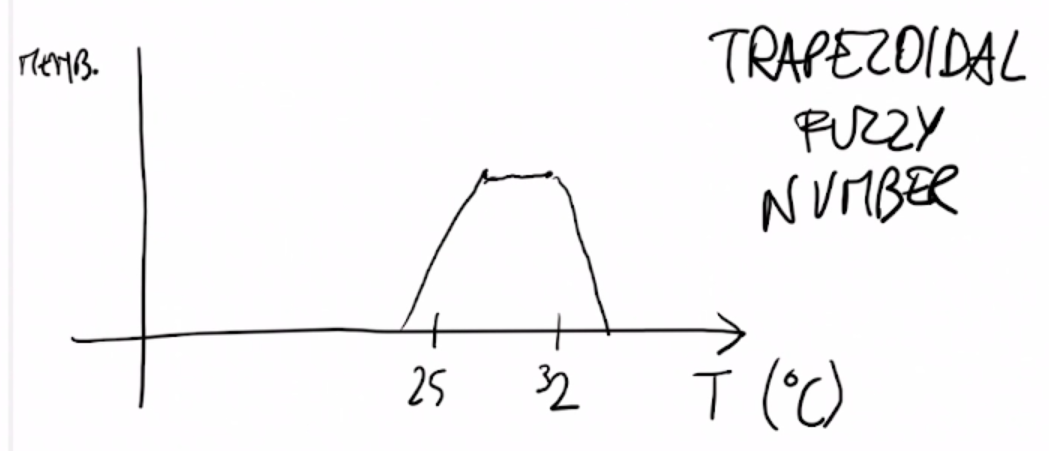
È possibile definire un insieme di operazioni numeriche tra i numeri Fuzzy (come addizione ecc) con un meccanismo che si chiama principio di estensione -> il risultato dell'operazione tra due numeri fuzzy è un numero fuzzy.
Utilizzate ad esempio negli elettrodomestici -> "se la temperatura è alta e la pressione è bassa allora la velocità della ventola è intermedia"
Ciascun aggettivo corrisponde ad un insieme fuzzy (o ad un numero fuzzy).
Queste regolo permettono di non discretizzare in intervalli i vari valori per cui definire alta, bassa e intermedia.
Immaginare un insieme di regole fuzzy per decidere la velocità del motore. Bisogna calcolare per ogni regola il valore di attivazione della regola (cioè quanto è vero l'antecedente) -> il valore finale è ovviamente un insieme Fuzzy.