COMPiLELab / HOLaGraF

The code for Higher-Order Laplacian Gradient Flow for "Quantifying the structural stability of simplicial homology" by N.Guglielmi, A.Savostianov and F.Tudisco

HOLaGraF: Topological Stability for higher-order graph Laplacian operators

This repository provides the code for Higher-Order Laplacian Gradient Flow for "Quantifying the structural stability of simplicial homology" by Nicola Guglielmi, Anton Savostianov and Francesco Tudisco.

We provide the documentation and examples for the implementation of the gradient flow algorithm in julia. The implementation in matlab that supports a similar code structure will be uploaded later.

Background

We advise to consult the companion paper:

"Quantifying the structural stability of simplicial homology" by Nicola Guglielmi, Anton Savostianov and Francesco Tudisco.

Current work defines the topoligical stability of the homology group on generalized networks: briefly, we aim to increase the number of 1-dimensional holes in the simplicial complex $\mathcal{K}$ though increasing the dimension of the kernel of corresponding higher-order Laplacian operator $\overline{L}_1$ formed by boundary operators $B_1$ and $B_2$, weighted and normalized.

The minimal perturbation $(\varepsilon, E)$ affecting the graph's homology is found through the gradient flow optimization of the target spectral functional:

$$ F(\varepsilon, E) = \frac{1}{2} \lambda_+^2(\overline{L}_1) + \frac{\alpha}{2} \max \left( 0, 1-\frac{\mu_2(L_0)}{\mu} \right)^2 $$

Minimal working example

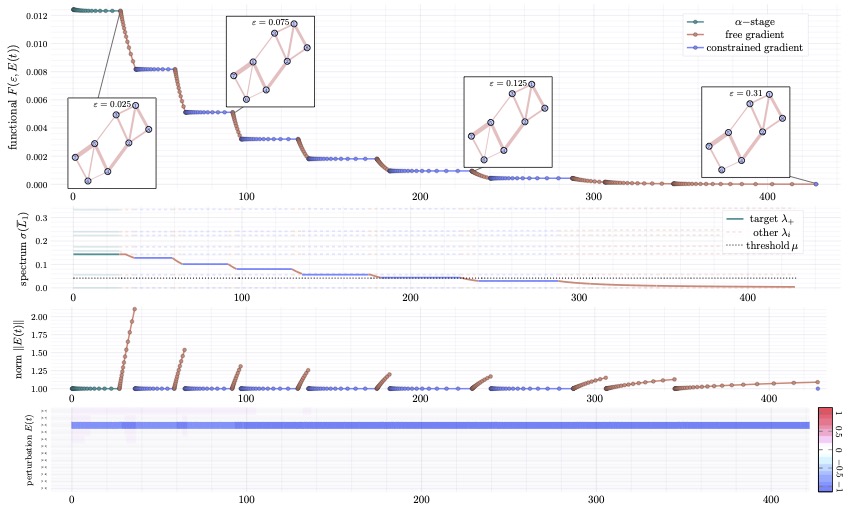
Here we provide a minimal working example of the alternating constrained- and free- gradient flow optimization procedure developed in the paper.

using BenchmarkTools, Printf  # quality of life libs
using LinearAlgebra, Arpack
include("HOLaGraF_lsmr.jl")  # import of the main library
using .HOLaGraF_lsmr

The graph is defined by the list edges, triangles (read from files) and number of vertices. Weights of the edges are assigned manually; initial perturbation e (the diagonal of E(t)) is given with a zero-initial norm:

n = 8;
edges = readMatrix("julia/example/8.edges")
trigs = readMatrix("julia/example/8.trigs")
w = reshape([0.5; 0.95; 1.0; 1.0; 1.0; 1.1; 1.1; 1.1; 1.05; 0.31; 1.05; 0.9].^2, :, 1);
ε0 = 1e-8; e = -ones(size(w, 1)); e = e/norm(e, 2);

G=NiceGraph(n, edges, trigs, w, ε0, e, nothing);

The mutable structure (class-like) generates the network in form of B1 and B2 boundary operators and points object generated with the spring layout (unless specified by the user).

The sturcture Thresh constains parameters of the functional α (will be changed throughout the alpha-phase) and μ (given as a share of the initial algebraic connectivity):

L0 = getL0(G);
μ = eigs(L0, nev = 2, which = :SR)[1][2];
thrs = Thresh( 0.75*μ, 1.0 );

In order to run the algorithm, it is sufficient to call the function wrapper: it follows the algorithm defined the paper:

include("wrapper.jl");
inFun = placeL1up(I(size(G.edges, 1)));   # example run without the preconditioner

h0 = 0.1;
ε_Δ=0.025;
G.eps0 = ε_Δ;

logSizes = Vector{Float64}(); logSteps = Vector{Float64}(); logTrack = Vector{Float64}();
logE = Array{Float64}(undef, size(G.w, 1), 0); logΛ = Array{Float64}(undef, size(G.w, 1), 0);

α_st, α_fin = 1.0, 100.0;

@time G, thrs, logSizes, logSteps, logTrack, logE, logΛ = wrapper(G, h0, α_st, α_fin, thrs, ε_Δ, logSizes, logSteps, logTrack, logE, logΛ, inFun );

• logSteps keeps track of all the steps per iteration;
• logSizes keeps track of number of Euler steps in each iteration;
• logTrack stores decreasing functional along the flow;
• logE stores the perturbation profile along the flow;
• logΛ stores the change of the spectrum

We do not encourage the usage of logΛ since it calls for a full spectrum at each Euler step. In the computationally demanding cases we suggest avoiding full spectrum computation!

NiceGraph.jl as a graph structure

• n, edges, trigs – the number of vertices, lists of edges and triangles;
• B1, B2 – unnormalized initial boundary operators; generated by B1fromEdges and B2fromTrigs functions;
• w – initial edges' weight profile;
• eps0 and e – the perturbation norm and the perturbation shape (the main diagonal);
• points – vertices' coordinates; either provided by user or generated by springLayout.

thrs_struct.jl as a parameter dictionary

• alph – the penalisation weight from the target functional;
• mu – the threshold for the homological pollution.

generateDelaunay.jl functionality

We also provide the code to sample the triangulation-based synthetic dataset based on the Delaunay triangulation.

• Vertice samplign and triangulation: function generateDelauney(N) builds a triangulation network with $N+4$ vertices and returns vertices' coordinates with lists of edges and triangles;
• Removal an edge from the network: pair of functions getIndx2Kill(edges) and killEdge(indx, n, edges, trigs) sample the number of edge to eliminate (without the outer border) and eliminate it from the edge list with all adjacent triangles;
• Addition of an edge: pair of functions getNewEdge(n, edges) and addEdge(new_edge, n, edges, trigs) sample a new edge (not yet present in the edge list) and add it to the edge list with all the newly formed triangles.

One can find bulk launch of sampling + HOLaGraF run in fullTriangleRun.jl.

Dependencies for julia code

Full list of dependecies:

using SparseArrays, LinearAlgebra, Arpack, Krylov, ArnoldiMethod  #linear algebra libraries
using SuiteSparse, IncompleteLU, LimitedLDLFactorizations, ILUZero # OPTIONAL: various preconditioners
using LinearMaps, LinearOperators # functional libraries to create linear operators
using GR, StatsBase  # Delaunay triangulation
using DelimitedFiles, DataFrames, CSV # reading from files
using Random, Printf, BenchmarkTools