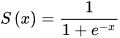AbnerHung / Logistic_Regression

从0开始的逻辑回归python实现

使用pytorch生成数据示例：

n_data = torch.ones(1000, 2)
xx = torch.ones(2000)
# print(xx)
x0 = torch.normal(2 * n_data, 1)  # 生成均值为2.标准差为1的随机数组成的矩阵 shape=(100, 2)
y0 = torch.zeros(1000)
x1 = torch.normal(-2 * n_data, 1)  # 生成均值为-2.标准差为1的随机数组成的矩阵 shape=(100, 2)
y1 = torch.ones(1000)

#合并数据x,y
x = torch.cat((x0, x1), 0).type(torch.FloatTensor)
y = torch.cat((y0, y1), 0).type(torch.FloatTensor)
y = torch.unsqueeze(y, 1) # 使y的shape=（2000，2）
x = x.numpy() # 转numpy
x = np.insert(x, 0, xx, axis=1) # 在所有行第一列前插入1
x_t = x[1500:2000, :] # 手动划分测试集，下同
x = x[0:1499, :]
y = y.numpy()
y_t = y[1500:2000, :]
y = y[0:1499, :]

定义sigmoid函数

sigmoid函数如图： 使用numpy实现：

def sigmoid(x):
    return (1/ (1+ np.exp(-x )))

定义model函数

model返回预测结果，如下图示

返回X张量乘以theta的转置，代码如下

def model(x,theta):
    return sigmoid(np.dot(x,theta.T))

定义损失函数

逻辑回归使用二分交叉熵损失

Out = -1 * weight * (label * log(input) + (1 - label) * log(1 - input))

使用numpy矩阵乘法等操作可以实现：

def cost(x, y, theta):
    left = np.multiply(-y, np.log(model(x, theta)))
    right = np.multiply((1 - y), np.log(1 - model(x, theta)))
    num = len(x)
    return (np.sum(left - right) / num)