Giters

0xgleb / de-coursework

A-level Differential Equations Airplane landing modelling coursework

Geek Repo:Geek Repo

Github PK Tool:Github PK Tool

\begin{titlepage} \begin{center} \line(1,0){300}
[5mm] \huge{\bfseries Differential Equations Coursework} \ \huge{Aeroplane Landing Modelling} \ [5mm] \huge{Gleb Dianov} \ \end{center} \end{titlepage}

\newpage

\tableofcontents

\newpage

Simplifying situation and setting up the model

Given data

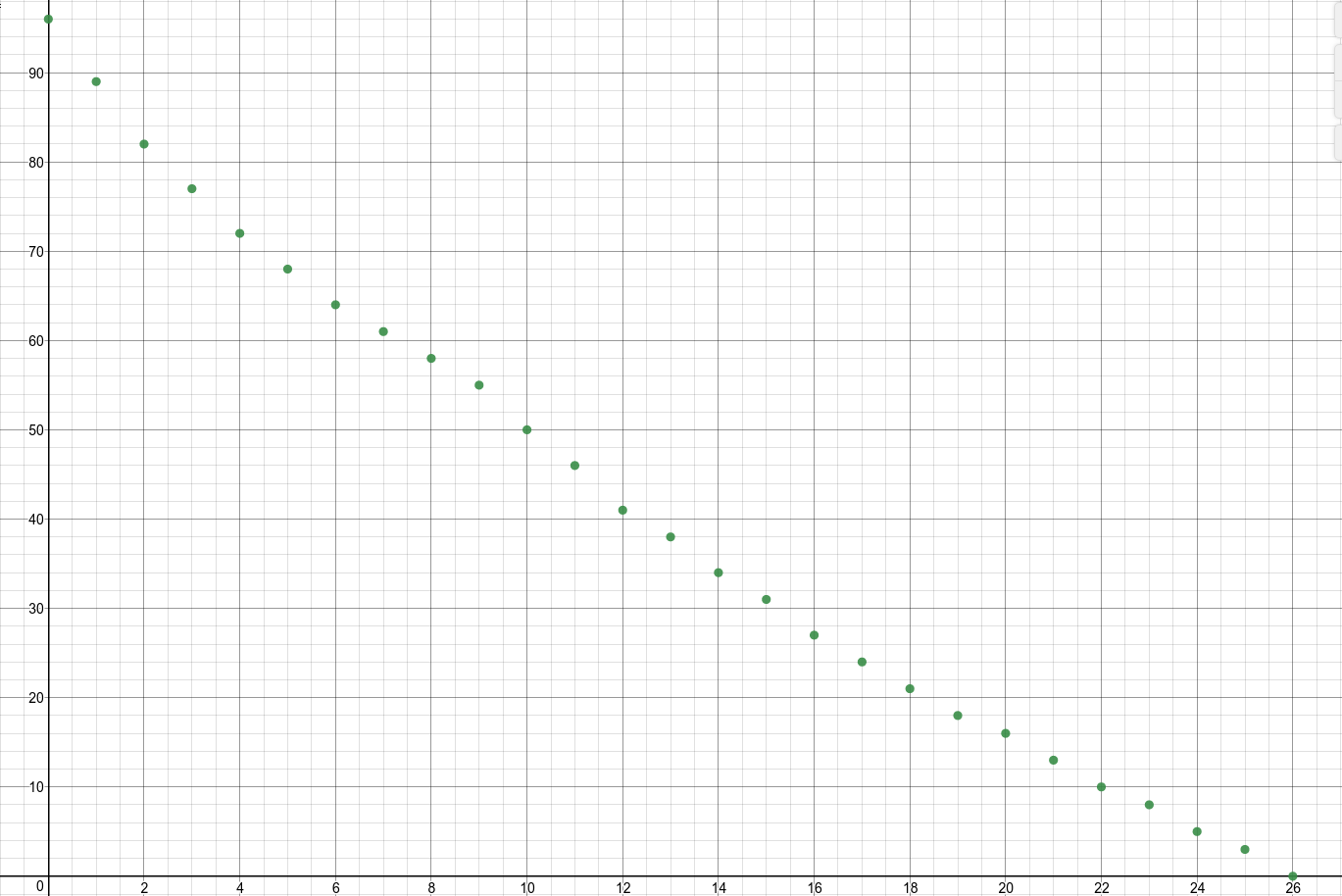
I’ve been given data about a landing aeroplane after touchdown. The mass of the aeroplane is $120 000$ kg. Initially air resistance slows the aeroplane and then, when it is slow enough, wheel brakes add a constant force to fully stop the aeroplane. The table below shows the aeroplane’s speed, $v$ ms-1, $t$ seconds after touchdown.

tvtv
0961434
1891531
2821627
3771724
4721821
5681918
6642016
7612113
8582210
955238
1050245
1146253
1241260
1338

The image below shows a chart of the original data.

./original_graph.png

Modeling assumptions

  • The aeroplane can be modeled as a point particle. This assumption allows us to negate any complex resistances that would occur. Modeling this way is appropriate because we are not given velocity (only speed) of the aeroplane at different points in time, so we are not interested in any rotations of the plane.
  • The runway can be modeled as a plane. Without this assumption we would need to consider the possibility that the runway has a complex shape, for example it can have hills and/or pits.
  • The runway is horizontal. Without this assumption we would need to include components of the weight and the reaction force in the model which would increase the complexity of the model and affect the calculations.
  • The aeroplane is moving in the horizontal plane. This assumption allows us to negate any vertical forces.
  • The constant force from the wheel brakes (after the brakes are applied) and the air resistance are the only forces acting on the aeroplane in the horizontal plane. This assumption allows us to say that any other resistance is negligible and there are no other forces, alternatively we can say that the air resistance model is a model of the total resistance force.
  • The given values for speed are rounded to the nearest integer. This assumption allows the model of speed to have an error $±0.5$. It’s very unlikely that the values of speed are exactly integers, so it’s a reasonable assumption.
  • Brakes are applied at $t = 9$. The table below shows differences between consecutive speed values, $Δ v$, and differences between consecutive differences, $Δ (Δ v)$. $Δ (Δ v)$ is the lowest when $t = 10$. This means that the highest decrease of acceleration occurred between $t = 9$ and $t = 10$, hence we will assume that the brakes were applied during that time. We will model this as if the brakes were applied at $t = 9$.
tvΔ vΔ (Δ v)tvΔ vΔ (Δ v)
0961434-4-1
189-71531-31
282-701627-4-1
377-521724-31
472-501821-30
568-411918-30
664-402016-21
761-312113-3-1
858-302210-30
955-30238-21
1050-5-2245-3-1
1146-41253-21
1241-5-1260-3-1
1338-32
  • Braking force starts working instantly. This assumption makes acceleration not continuous and simplifies the calculations.
  • There is no wind. This allows us to assume that if the plane is not moving then there is no air resistance.

\newpage

Derivation of the initial model

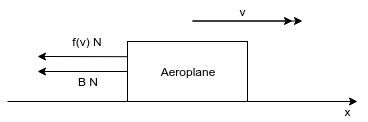
./plane_diagram.png

The diagram shows the x-axis, direction of velocity, $v$, the air resistance, $f(v)$, and the constant braking force (when brakes are used), $B$.

$$ F = ma \mbox{ (Newton’s second law)} $$ $$ F = \begin{cases} - f(v), & 0 \leq t < 9 \ - f(v) - B, & 9 \leq t \leq 26 \end{cases} $$ $$ a = \dot{v} $$ $$ ⇒ \begin{cases} m\dot{v} = - f(v), & t < 9 \ m\dot{v} = - f(v) - B, & t \geq 9 \end{cases} $$ $$ \mbox{where } m = 120 000 $$

Model 1

Defining f(v)

As you can see in the table with the differences, speed for $t ∈ (0, 9)$ clearly isn’t decreasing linearly. And you can see that, as speed decreases (in that interval), the rate at which it decreases also decreases. So it’s reasonable to suggest that

$$ f(v) \propto v^2 $$ $$ ⇒ f(v) = kv^2 $$ $$ ⇒ m\dot{v} = \begin{cases} - kv^2, & 0 \leq t < 9 \ - kv^2 - B, & 9 \leq t \leq 26 \end{cases} $$

To make $v$ continuous I will assume that both models are valid for $t = 9$.

$$ m\dot{v} = \begin{cases} - kv^2, & 0 \leq t \leq 9 \ - kv^2 - B, & 9 \leq t \leq 26 \end{cases} $$

General solution

0 \leq t \leq 9

$$ m\dot{v} = -kv^2 $$ $$ ⇒ m\frac{\dot{v}}{v^2} = -k $$ $$ ⇒ m∫ \frac{\dot{v}}{v^2} dt = -k∫ dt $$ $$ ⇒ m∫ v-2 dv = -kt + c_1 $$ $$ ⇒ m\frac{v-1}{-1} = -kt + c_1 $$ $$ ⇒ \frac{-m}{v} = -kt + c_1 $$ $$ ⇒ v = \frac{m}{kt - c_1} $$

9 \leq t \leq 26

$$ m\dot{v} = -kv^2 - B $$ $$ m\frac{\dot{v}}{kv^2 + B} = -1 $$ $$ m∫ \frac{\dot{v}}{kv^2 + B} dt = -∫ dt $$ $$ m∫ \frac{1}{kv^2 + B} dv = -∫ dt $$ $$ arctan’(ψ) = \frac{1}{ψ^2 + 1} $$ $$ ⇒ arctan’(\frac{a}{b}ψ) = \frac{a}{b} × \frac{1}{(\frac{a}{b}ψ)^2 + 1} = \frac{a}{b} × \frac{b^2}{a^2ψ^2 + b^2} = \frac{ab}{a^2ψ^2 + b^2} $$ $$ ⇒ arctan’(\sqrt{\frac{a}{b}}ψ) = \frac{\sqrt{ab}}{aψ^2 + b} $$ $$ ⇒ ∫ \frac{1}{kv^2 + B} dv = \frac{1}{\sqrt{kB}}∫ \frac{\sqrt{kB}}{kv^2 + B} = \frac{arctan(\sqrt{\frac{k}{B}}v)}{\sqrt{kB}} + c $$ $$ ⇒ \frac{marctan(\sqrt{\frac{k}{B}}v)}{\sqrt{kB}} = -t + c $$ $$ ⇒ \sqrt{\frac{k}{B}}v = tan \frac{\sqrt{kB}(-t + c)}{m} $$ $$ ⇒ v = \sqrt{\frac{B}{k}} tan \frac{\sqrt{kB}(-t + c)}{m} $$ $$ \mbox{Let } c_2 = \sqrt{kB}c $$ $$ ⇒ v = \sqrt{\frac{B}{k}} tan(\frac{c_2 -\sqrt{kB}t}{m})$$ $$ ⇒ v = \begin{cases} \frac{m}{kt - c_1}, & 0 \leq t \leq 9 \ \sqrt{\frac{B}{k}} tan(\frac{c_2 -\sqrt{kB}t}{m}), & 9 \leq t \leq 26 \end{cases} $$

Particular solution

The general solution has 4 unknown constants: the constant braking force, $B$, the coefficient from the air resistance model, $k$, and 2 constants of integration from solving the 2 differential equations, $c_1$ and $c_2$. To make $v$ continuous I will use point $(t = 9, v = 55)$.

$$ \begin{cases} \frac{m}{9k - c_1} = 55 \ \sqrt{\frac{B}{k}} tan \frac{c_2 - 9\sqrt{kB}}{m} = 55 \end{cases} $$ $$ ⇒ 9k - c_1 = \frac{m}{55} $$ $$ ⇒ k = \frac{c_1 + \frac{m}{55}}{9} $$ $$ S \mbox{ is the set of given data.} $$ $$ (t_1, v_1), (t_2, v_2) ∈ S; t_1, t_2 \leq 9, t_1 ≠ t_2 $$ $$ \begin{cases} v_1 = \frac{m}{t_1k - c_1} \ v_2 = \frac{m}{t_2k - c_1} \end{cases} $$ $$ ⇒ \begin{cases} v_1v_2t_2t_1k - v_1v_2t_2c_1 = mv_2t_2 \ v_1v_2t_1t_2k - v_1v_2t_1c_1 = mv_1t_1 \end{cases} $$ $$ ⇒ c_1v_1v_2(t_2 - t_1) = m(v_1t_1 - v_2t_2) $$ $$ ⇒ c_1 = \frac{m(v_1t_1 - v_2t_2)}{v_1v_2(t_2 - t_1)} $$ $$ \sqrt{\frac{B}{k}} tan \frac{c_2 - 9\sqrt{kB}}{m} = 55 $$ $$ ⇒ c_2(B) = marctan(\frac{55k\sqrt{\frac{B}{k}}}{B}) + 9\sqrt{Bk} $$ $$ (t_3, v_3) ∈ S; t_3 > 9 $$ $$ ⇒ v_3 = \sqrt{\frac{B}{k}} tan \frac{c_2(B) - \sqrt{kB}t_3}{m} $$ $$ ⇒ arctan(v_3\sqrt{\frac{k}{B}}) = \frac{c_2(B) - \sqrt{kB}t_3}{m} $$ $$ \mbox{Let } λ(B) = \frac{c_2(B) - \sqrt{kB}t_3}{m} - arctan(v_3\sqrt{\frac{k}{B}}) $$ $$ \mbox{Newton-Raphson’s rule: } Bn+1 = B_n + \frac{λ’(B_n)}{λ(B_n)} $$ \begin{equation} \begin{cases} c_1 = \frac{m(v_1t_1 - v_2t_2)}{v_1v_2(t_2 - t_1)}
k = \frac{c_1 + \frac{m}{55}}{9} \ c_2(B) = marctan(\frac{55k\sqrt{\frac{B}{k}}}{B}) + 9\sqrt{Bk} \ λ(B) = \frac{c_2(B) - \sqrt{kB}t_3}{m} - arctan(v_3\sqrt{\frac{k}{B}}) \ Bn+1 = B_n - \frac{λ(B_n)}{λ’(B_n)} B_0 = 300000 \end{cases} \end{equation}

To find $B_0$ I used a graphing web app. First I put in all the formulas and given data points. $v(0) = \frac{m}{- c_1} &gt; 0$, hence $c_1 &lt; 0$. I started decreasing $c_1$ until it roughly matched first 10 points. $B &gt; 0$, so for this value of $c_1$ I started increasing $B$ until I found that $B ≈ 300,000$.

./img/not_optimized_first_model.png

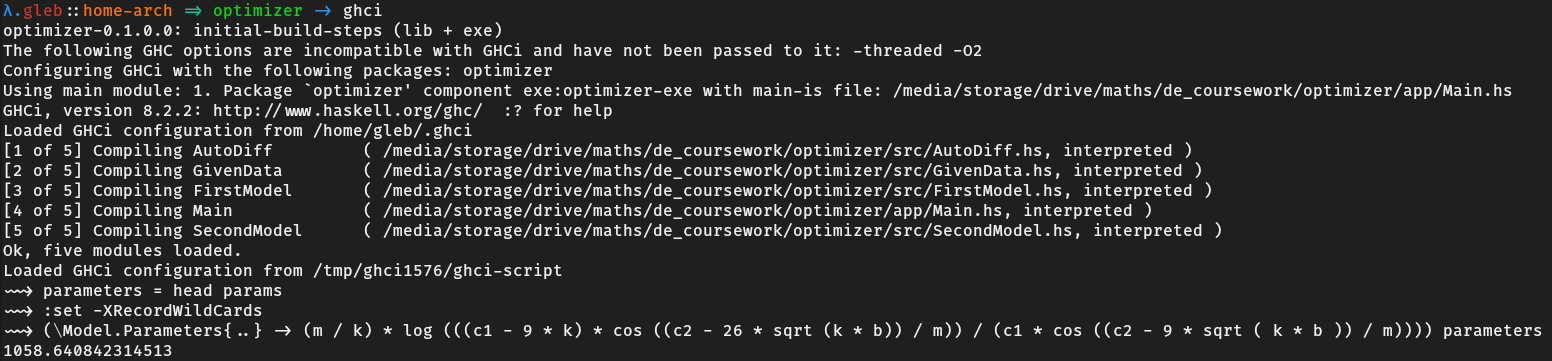
Now I can use programming to find the parameters. To do this I wrote 5 modules in Haskell. The first module is a module for automatic differentiation using dual numbers and Newton-Raphson method.

The second module contains the given data.

\newpage

Then I defined a general interface for models.

The fourth module is for the first model and finding parameters.

And finally the main module, which runs this code to find the parameters.

import           Data.List      (sort, sortOn)
import           Data.Proxy

import           GivenData
import qualified Solution.First as Sol
import           Solution.Model as Model

adjustLength :: (a -> String) -> (a -> String -> b) -> [a] -> [b]
adjustLength g s l =
  (\x -> let str = g x in s x $ str ++ replicate (longest - length str) ' ') <$> l
  where longest = maximum $ length . g <$> l

showPredictions :: (ModelParams f, Show (f Double)) => f Double -> String
showPredictions params =
  foldMap (\(x, y, z, w) -> "| " ++ x ++ " | " ++ y ++ " | " ++ z ++ " | " ++ w ++ " |\n")
     $  adjustLength (\(_, _, _, w) -> w) (\(x, y, z, _) w -> (x, y, z, w))
     $  adjustLength (\(_, _, z, _) -> z) (\(x, y, _, w) z -> (x, y, z, w))
     $  adjustLength (\(_, y, _, _) -> y) (\(x, _, z, w) y -> (x, y, z, w))
     $  adjustLength (\(x, _, _, _) -> x) (\(_, y, z, w) x -> (x, y, z, w))
     $  (("Time", "Predicted Speed", "Rounded predicted speed", "Observed Speed"):)
     $  (\(Point t v) -> let v' = predict params t in (show t, show v', rounded v', rounded v))
    <$> points
  where rounded = show . round

maxErr :: (a -> Double -> Double) -> a -> Double
maxErr predict params =
  maximum $ abs . (\(Point t v) -> predict params t - v) <$> points
  where n = fromIntegral (length points)

avrErr :: (a -> Double -> Double) -> a -> Double
avrErr predict params =
  (/ n) $ sum $ abs . (\(Point t v) -> predict params t - v) <$> points
  where n = fromIntegral (length points)

rms :: (a -> Double -> Double) -> a -> Double
rms predict params =
  (/ n) $ sqrt $ sum $ (^2) . (\(Point t v) -> predict params t - v) <$> points
  where n = fromIntegral (length points)

showErrors :: (ModelParams f, Show (f Double)) => f Double -> String
showErrors params =
  foldMap (\(x, y, z) -> "| " ++ x ++ " | " ++ y ++ " | " ++ z ++ " |\n")
  $  adjustLength (\(_, _, z) -> z) (\(x, y, _) z -> (x, y, z))
  $  adjustLength (\(_, y, _) -> y) (\(x, _, z) y -> (x, y, z))
  $  adjustLength (\(x, _, _) -> x) (\(_, y, z) x -> (x, y, z))
  [ ("Maximum Error", "Average Error", "Root mean square")
  , (show $ maxErr predict params, show $ avrErr predict params, show $ rms predict params)
  ]

showResults :: (ModelParams f, Show (f Double)) => f Double -> String
showResults params = show params ++ "\n"
                  ++ showErrors params ++ "\n"
                  ++ showPredictions params

results :: [Sol.Parameters Double]
results =  sortOn (rms predict) $ findParams
      <$> combinations (Proxy :: Proxy Sol.Parameters)

main :: IO ()
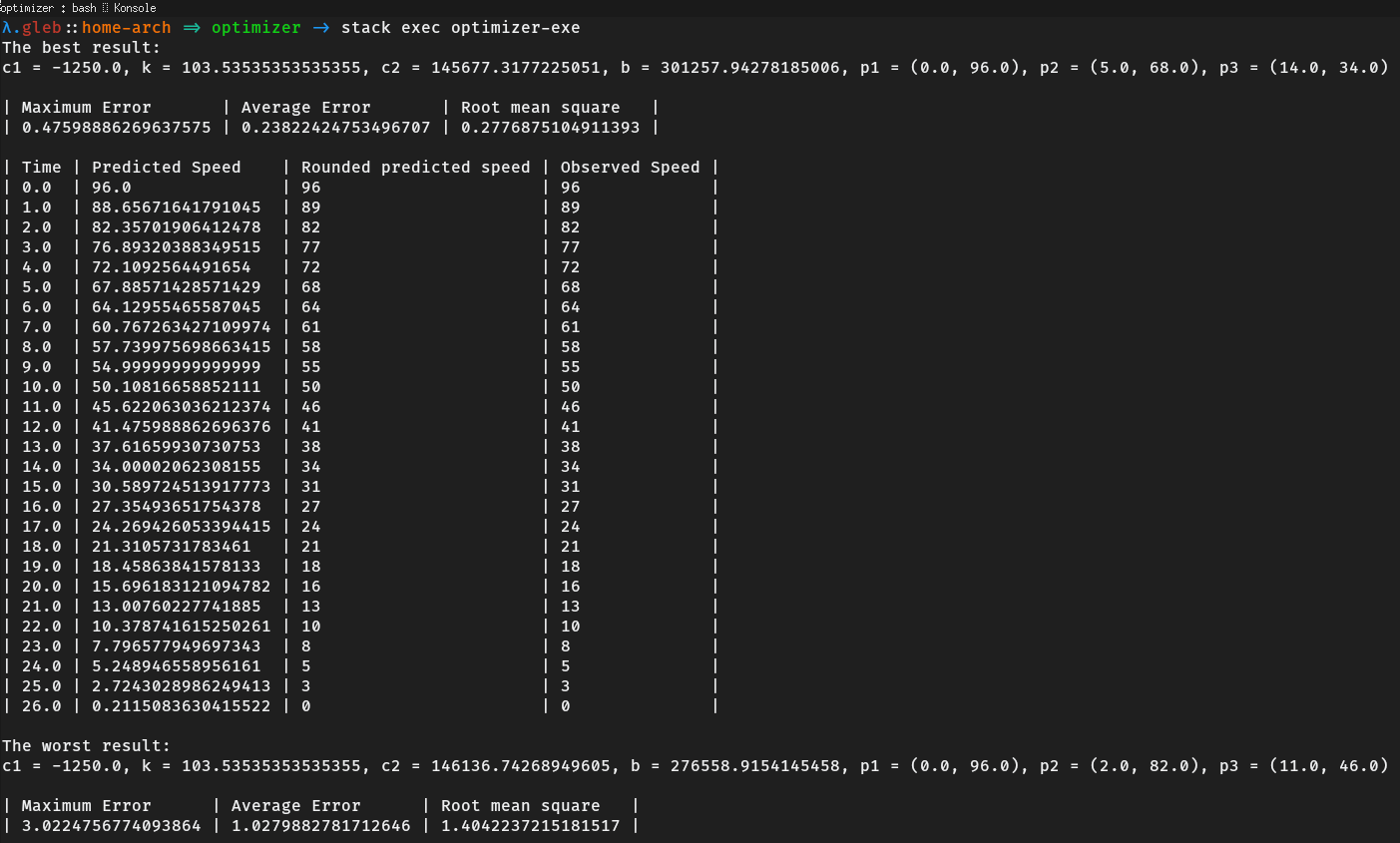
main = do putStrLn "The best result:"
          putStrLn $ showResults $ head results
          putStrLn "The worst result:"
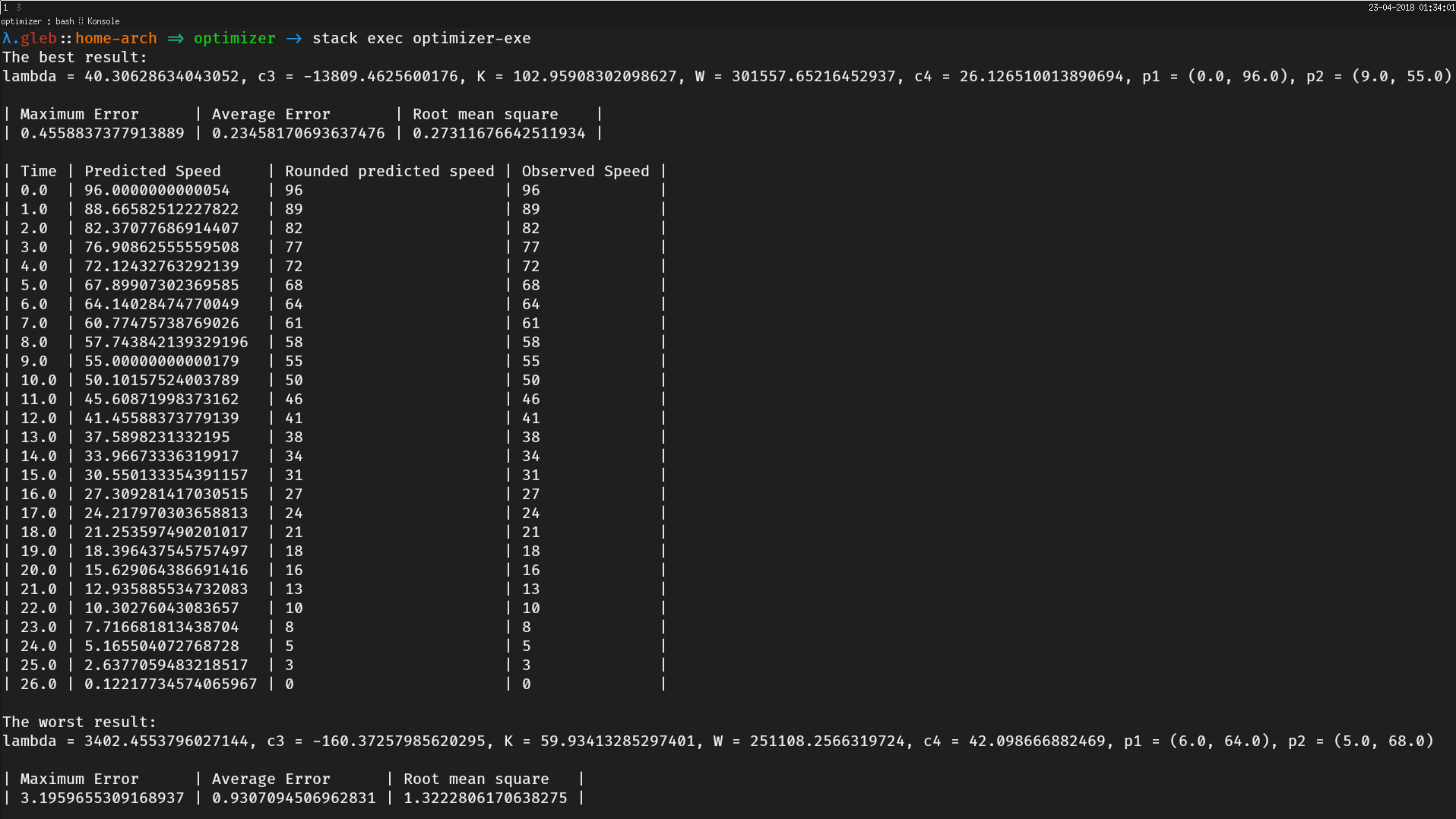
          putStr   $ showResults $ last results

Here is the result. It shows the best and the worst parameters found using the derived formulas and for both of the configurations it shows sums of squares of errors, and predictions for each of the given point with rounded versions.

./img/first_model_code_result.png

Graphs and Analysis

TimePredictedRoundedObserved
SpeedPredictedSpeed
Speed
0.096.09696
1.088.656716417910458989
2.082.357019064124788282
3.076.893203883495157777
4.072.10925644916547272
5.067.885714285714296868
6.064.129554655870456464
7.060.7672634271099746161
8.057.7399756986634155858
9.054.999999999999995555
10.050.108166588521115050
11.045.6220630362123744646
12.041.4759888626963764141
13.037.616599307307533838
14.034.000020623081553434
15.030.5897245139177733131
16.027.354936517543782727
17.024.2694260533944152424
18.021.31057317834612121
19.018.458638415781331818
20.015.6961831210947821616
21.013.007602277418851313
22.010.3787416152502611010
23.07.79657794969734388
24.05.24894655895616155
25.02.724302898624941333
26.00.211508363041552200
Maximum ErrorAverage ErrorRoot mean square
0.475988862696375750.238224247534967070.2776875104911393

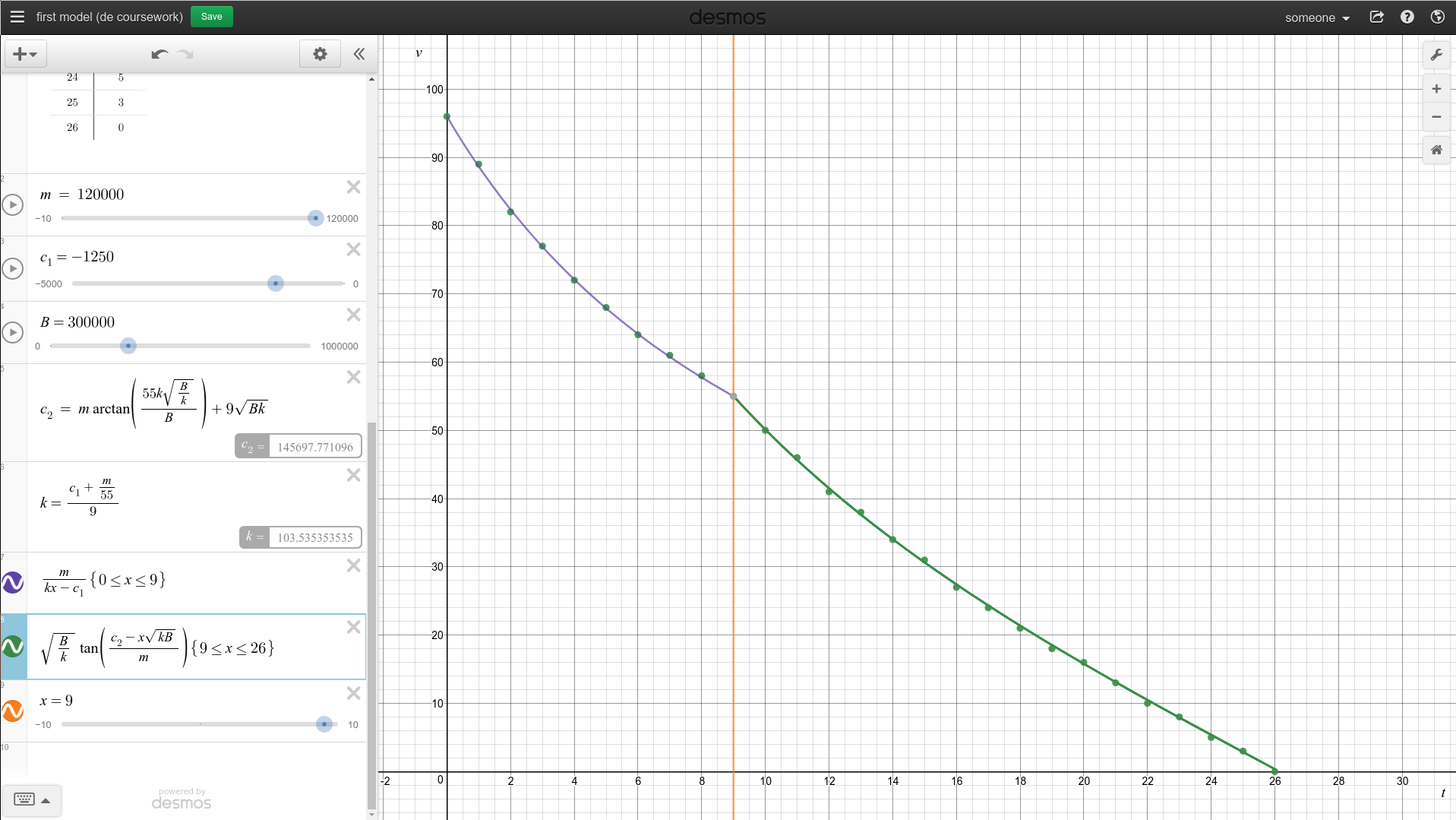
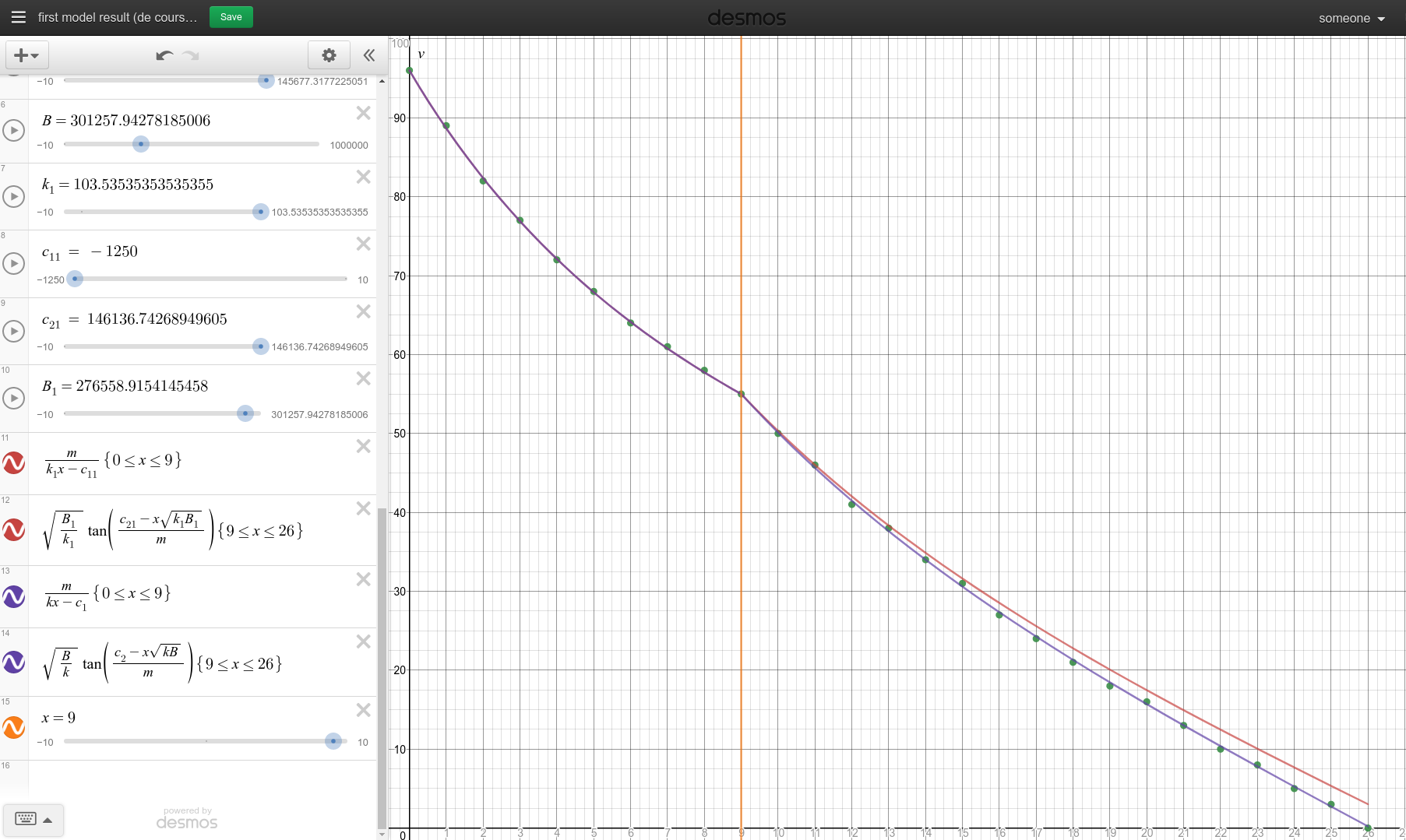
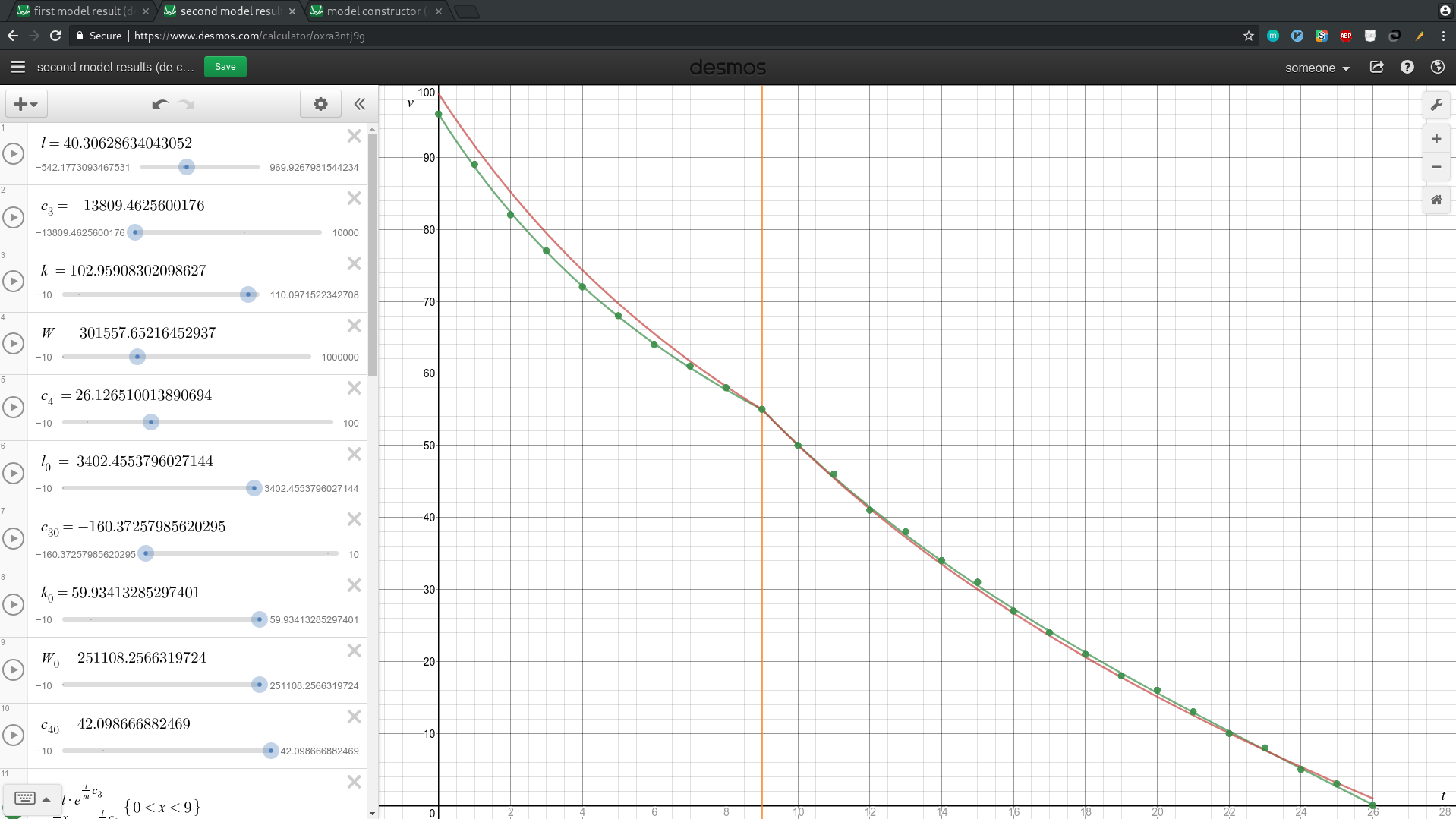
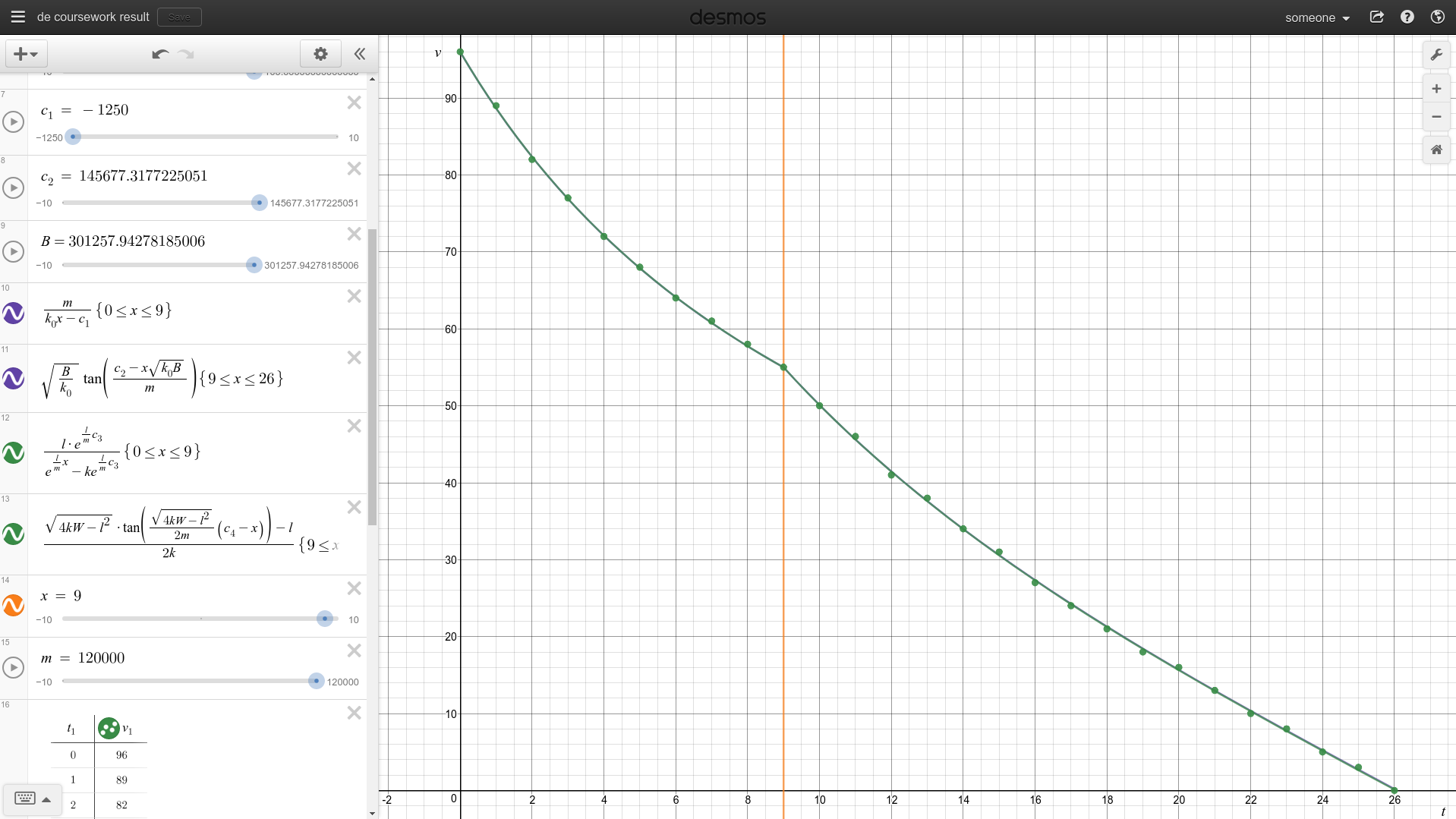
I’ll now look at the two configurations that I obtained and plot them. The red line shows the worst configuration, and the purple line shows the best configuration.

./img/first_model_graph_result.png

As you can see in first_model_code_result rounded predictions of the best configuration exactly match the given data.

Conclusion of Model 1

\begin{equation} \begin{cases} v(t) = \frac{m}{kt - c_1}, & 0 \leq t \leq 9
v(t) = \sqrt{\frac{B}{k}} tan(\frac{c_2 -\sqrt{kB}t}{m}), & 9 \leq t \leq 26 \ c_1 = -1250.0 \ k = 103.\dot{5}\dot{3} \ c_2 = 145677.3177225051 \ B = 301257.94278185006 \ \end{cases} \end{equation}

$$ x = ∫_026 v dt = ∫_0^9 v dt + ∫_926 v dt $$ $$ ∫ \frac{m}{kt - c_1} dt = \frac{m}{k} ∫ \frac{k}{kt - c_1} dt = \frac{m}{k}ln(kt - c_1) + \mbox{constant} $$ $$ ∫ \sqrt{\frac{B}{k}}tan(\frac{c_2 -\sqrt{kB}t}{m}) dt = \sqrt{\frac{B}{k}} × \frac{-m}{\sqrt{kB}} ∫ tan(\frac{c_2 - \sqrt{kB}t}{m})×\frac{-\sqrt{kB}}{m} dt =$$ $$ = \frac{m}{k} ∫ \frac{-sin(u)}{cos{u}} du = \frac{m}{k} ln(cos(\frac{c_2 - \sqrt{kB}t}{m})) + \mbox{constant} $$ $$ ⇒ x = \left[\frac{m}{k}ln(kt - c_1)\right]_0^9 + \left[\frac{m}{k} ln(cos(\frac{c_2 - \sqrt{kB}t}{m}))\right]_926 = \frac{m}{k}\left(ln(\frac{c_1 - 9k}{c_1}) + ln(\frac{cos(\frac{c_2 - 26\sqrt{kB}}{m})}{cos(\frac{c_2 - 9\sqrt{kB}}{m})})\right) $$ $$ ⇒ x = \frac{m}{k}ln\left(\frac{(c_1 - 9k)cos(\frac{c_2 - 26\sqrt{kB}}{m})}{c_1cos(\frac{c_2 - 9\sqrt{kB}}{m})}\right) $$

./img/first_model_integral.png

$$ ⇒ x ≈ 1058.650842313513 ≈ 1060 $$

The aeroplane fully stops in approximately $1060$ meters after touchdown, hence the runway has to be at least $1060$ meters long. However, I would advise length of $2000$ to be safe even if conditions change, for example in case touchdown occurs further, there is wind, friction between the wheels and the runway is lower.

Model 2

Redefining f(v)

Although the first model fits the given data very well, I think this model can be improved. This time I will add a linear term to the air resistance function.

$$ f(v) = k v^2 + λ v $$ $$ ⇒ m\dot{v} = \begin{cases} - kv^2 - λ v, & 0 \leq t \leq 9 \ - kv^2 - λ v - B, & 9 \leq t \leq 26 \end{cases} $$

General solution

0 \leq t \leq 9

$$ m\dot{v} = -kv^2 - λ v $$ $$ ⇒ m∫ \frac{1}{kv^2 + λ v} dv = -t + c_3 $$ $$ kv^2 + λ v ≡ v(kv + λ) $$ $$ \frac{1}{v(kv + λ)} ≡ \frac{A}{v} + \frac{B}{kv + λ} $$ $$ ⇒ 1 ≡ A(kv + λ) + Bv $$ $$ ⇒ \begin{cases} A = \frac{1}{λ} \ B = -\frac{k}{λ} \end{cases} $$ $$ ⇒ \frac{1}{kv^2 + λ v} ≡ \frac{1}{λ v} - \frac{k}{k λ v + λ^2} ( ≡ \frac{k λ v + λ^2 - k λ v}{λ v (k λ v + λ^2)} ≡ \frac{λ^2}{λ^2(kv^2 + λ v)} ≡ \frac{1}{kv^2 + λ v} ) $$ $$ ⇒ ∫ \frac{1}{kv^2 - λ v} dv = \frac{1}{λ}∫ v-1 dv - \frac{1}{λ}∫ \frac{k}{kv + λ} dv $$ $$ ⇒ \frac{m}{λ}(ln(v) - ln(kv + λ)) = c_3 - t $$ $$ ⇒ ln(\frac{v}{kv + λ}) = \frac{λ}{m} (c_3 - t) $$ $$ ⇒ \frac{v}{kv + λ} = e\frac{λ{m} (c_3 - t)} $$ $$ ⇒ v = k e\frac{λ{m} (c_3 - t)} v + λ e\frac{λ{m} (c_3 - t)} $$ $$ v = \frac{λ e\frac{λ{m} (c_3 - t)}}{1 - k e\frac{λ{m} (c_3 - t)}} $$ $$ v = \frac{λ e\frac{λ{m} c_3}}{e\frac{λ{m} t} - ke\frac{λ{m}c_3}} $$

9 \leq t \leq 26

$$ m\dot{v} = -kv^2 - λ v - W $$ $$ ⇒ m∫ \frac{1}{kv^2 + λ v + W} dv = -∫ dt $$ $$ kv^2 + λ v + W = (\sqrt{k}v + \frac{λ}{2\sqrt{k}})^2 + W - \frac{λ^2}{4k} = (W - \frac{λ^2}{4k})((\frac{\sqrt{k}v + \frac{λ}{2\sqrt{k}}}{\sqrt{W - \frac{λ^2}{4k}}})^2 + 1) = (W - \frac{λ^2}{4k})((\frac{2kv + λ}{\sqrt{4kW - λ^2}})^2 + 1) $$ $$ \mbox{Let } h(x) = \frac{2kx + λ}{\sqrt{4kW - λ^2}} $$ $$ ⇒ h’(x) = \frac{2k}{\sqrt{4kW - λ^2}} $$ $$ arctan’(x) = \frac{1}{1 + x^2} $$ $$ ⇒ (arctan(h(x)))’ = arctan’(h(x))h’(x) = \frac{1}{h^2(x) + 1}h’(x) = \frac{\frac{2k}{\sqrt{4kW - λ^2}}}{(\frac{2kx + λ}{\sqrt{4kW - λ^2}})^2 + 1} $$ $$ ⇒ m∫ \frac{1}{kv^2 + λ v + W} dv = m∫ \frac{1}{(W - \frac{λ^2}{4k})((\frac{2kv + λ}{\sqrt{4kW - λ^2}})^2 + 1)} dv = \frac{2m\sqrt{4kW - λ^2}}{4k(W - \frac{λ^2}{4k})}∫ \frac{\frac{2k}{\sqrt{4kW - λ^2}}}{(\frac{2kv + λ}{\sqrt{4kW - λ^2}})^2 + 1} dv $$ $$ ⇒ \frac{2m}{\sqrt{4kW-λ^2}}arctan(\frac{2kv + λ}{\sqrt{4kW - λ^2}}) = -t + c_4 $$ $$ ⇒ \frac{2kv + λ}{\sqrt{4kW - λ^2}} = tan(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - t)) $$ $$ ⇒ v = \frac{\sqrt{4kW - λ^2}tan(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - t)) - λ}{2k} $$ $$ ⇒ v = \begin{cases}\frac{λ e\frac{λ{m} c_3}}{e\frac{λ{m} t} - ke\frac{λ{m}c_3}}, & t ∈ [0, 9] \ \frac{\sqrt{4kW - λ^2}tan(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - t)) - λ}{2k}, & t ∈ [9, 26] \end{cases} $$

Particular solution

$$ ⇒ \begin{cases}\frac{λ e\frac{λ{m} c_3}}{e9\frac{λ{m}} - ke\frac{λ{m}c_3}} = 55 \ \frac{\sqrt{4kW - λ^2}tan(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - 9)) - λ}{2k} = 55 \end{cases} $$ $$ \mbox{Let } (t_1, v_1), (t_2, v_2) ∈ S; t_1, t_2 ∈ [0, 9]; t_1 ≠ t_2 $$ $$ \frac{λ e\frac{λ{m} c_3}}{et_1\frac{λ{m}} - ke\frac{λ{m}c_3}} = v_1 $$ $$ ⇒ v_1ke\frac{λ{m}c_3} = v_1et_1\frac{λ{m}} - λ e\frac{λ{m} c_3} $$ $$ ⇒ k = \frac{v_1et_1\frac{λ{m}} - λ e\frac{λ{m} c_3}}{v_1e\frac{λ{m}c_3}} $$ $$ ⇒ k = e\frac{λ{m}(t_1 - c_3)} - \frac{λ}{v_1} $$ $$ \frac{m}{λ}(ln(v_2) - ln(kv_2 + λ)) = c_3 - t_2 $$ $$ ⇒ c_3 = \frac{m}{λ}(ln(v_2) - ln(kv_2 + λ)) + t_2 $$ $$ ⇒ c_3 = \frac{m}{λ}(ln(\frac{v_2}{v_2 (e\frac{λ{m}(t_1 - c_3)} - \frac{λ}{v_1}) + λ})) + t_2 $$ $$ ⇒ e\frac{λ (c_3 - t_2){m}} = \frac{v_2}{v_2 (e\frac{λ{m}(t_1 - c_3)} - \frac{λ}{v_1}) + λ} $$ $$ ⇒ e\frac{λ{m}c_3}e-\frac{λ{m}t_2} = \frac{v_2}{v_2 (e\frac{λ{m}t_1}e-\frac{λ{m}c_3} - \frac{λ}{v_1}) + λ} $$ $$ ⇒ (v_2 e\frac{λ{m}t_1}e-\frac{λ{m}c_3} - v_2\frac{λ}{v_1} + λ)e\frac{λ{m}c_3}e-\frac{λ{m}t_2} = v_2 $$ $$ ⇒ v_2 e\frac{λ{m}(t_1 - t_2)} - (v_2\frac{λ}{v_1} - λ)e\frac{λ{m}(c_3 - t_2)} = v_2 $$ $$ ⇒ e\frac{λ{m}(c_3 - t_2)} = \frac{v_1v_2}{λ(v_2 - v_1)} (e\frac{λ{m}(t_1 - t_2)} - 1) $$ $$ ⇒ e\frac{λ{m}c_3} = \frac{v_1v_2}{λ(v_2 - v_1)} (e\frac{λ{m}t_1} - e\frac{λ{m}t_2}) $$ $$ ⇒ c_3 = \frac{m}{λ}ln(\frac{v_1v_2(e\frac{λ{m}t_1} - e\frac{λ{m}t_2})}{λ(v_2 - v_1)}) $$ $$ ⇒ k = e\frac{λ{m}(9 - c_3)} - \frac{λ}{55} \mbox{ (to make } v \mbox{ continuous)} $$ $$ \hat{v} = \frac{λ e\frac{λ{m} c_3}}{e\frac{λ{m} t} - ke\frac{λ{m}c_3}} $$ $$ J = ∑(t,v) ∈ S, t \leq 9 (\hat{v} - v)^2 $$

$J$ is a sum of squares of all errors for $t \leq 9$. We want to minimize this sum, so I will set its partial derivative to zero to find the value of $λ$ that minimizes $J$.

$$ \mbox{Let } ζ(λ) = \frac{∂ J}{∂ λ} = 0 $$ $$ ⇒ ζ(λ) = ∂λ∑(t,v) ∈ S, t \leq 9 (\hat{v} - v)^2 $$ $$ λn+1 = λ_n - \frac{ζ(λ)}{ζ’(λ)} \mbox{ (Newton-Raphson method)} $$ $$ \frac{\sqrt{4kW - λ^2}tan(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - 9)) - λ}{2k} = 55 $$ $$ ⇒ \sqrt{4kW - λ^2}tan(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - 9)) = 2k55 + λ $$ $$ ⇒ \frac{\sqrt{4kW-λ^2}}{2m}(c_4 - 9) = arctan(\frac{2k55 + λ}{\sqrt{4kW - λ^2}}) $$ $$ ⇒ c_4 = 9 + \frac{2marctan(\frac{2k55 + λ}{\sqrt{4kW - λ^2}})}{\sqrt{4kW-λ^2}} $$ $$ \frac{\sqrt{4kW-λ^2}}{2m}(c_4 - t) = arctan(\frac{2kv + λ}{\sqrt{4kW - λ^2}}) $$ $$ ⇒ \frac{\sqrt{4kW-λ^2}}{2m}(c_4 - t) - arctan(\frac{2kv + λ}{\sqrt{4kW - λ^2}}) = 0 $$ $$ I = ∑(t,v) ∈ S, t \geq 9 \left(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - t) - arctan(\frac{2kv + λ}{\sqrt{4kW - λ^2}})\right)^2 $$

We want to minimize $I$.

$$ \mbox{Let } φ(W) = \frac{∂ I}{∂ W} = 0 $$ $$ ⇒ φ(W) = ∂_W ∑(t,v) ∈ S, t \geq 9 \left(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - t) - arctan(\frac{2kv + λ}{\sqrt{4kW - λ^2}})\right)^2 $$ $$ ⇒ Wn+1 = W_n - \frac{φ(W)}{φ’(W)} $$

I found $λ_0$ and $W_0$ the same way I found $B_0$ for the first model - I made a graph and adjusted parameters $c_3$, $λ$, and $W$ until the curve roughly fit the data.

./img/not_optimized_second_model.png

\begin{equation} \begin{cases} c_3 = \frac{m}{λ}ln(\frac{v_1v_2(e\frac{λ{m}t_1} - e\frac{λ{m}t_2})}{λ(v_2 - v_1)})
k = e\frac{λ{m}(9 - c_3)} - \frac{λ}{55} \ ζ(λ) = ∂λ∑(t,v) ∈ S, t \leq 9 (\frac{λ e\frac{λ{m} c_3}}{e\frac{λ{m} t} - ke\frac{λ{m}c_3}} - v)^2 \ λn+1 = λ_n - \frac{ζ(λ_n)}{ζ’(λ_n)} \ λ_0 = 921.7 \ c_4 = 9 + \frac{2marctan(\frac{110k + λ}{\sqrt{4kW - λ^2}})}{\sqrt{4kW-λ^2}} \ φ(W) = ∂_W ∑(t,v) ∈ S, t \geq 9 \left(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - t) - arctan(\frac{2kv + λ}{\sqrt{4kW - λ^2}})\right)^2 \ Wn+1 = W_n - \frac{φ(W)}{φ’(W)} \ W_0 = 290000 \end{cases} \end{equation}

I wrote another module for the second model:

I also changed import Solution.First as Sol to import Solution.Second as Sol in the main module. This code gives us the following result:

./img/second_model_code_result.png

Graphs and Analysis

TimePredictedRoundedObserved
SpeedPredictedspeed
Speed
0.096.00000000000549696
1.088.665825122278228989
2.082.370776869144078282
3.076.908625555595087777
4.072.124327632921397272
5.067.899073023695856868
6.064.140284747700496464
7.060.774757387690266161
8.057.7438421393291965858
9.055.000000000001795555
10.050.101575240037895050
11.045.608719983731624646
12.041.455883737791394141
13.037.58982313321953838
14.033.966733363199173434
15.030.5501333543911573131
16.027.3092814170305152727
17.024.2179703036588132424
18.021.2535974902010172121
19.018.3964375457574971818
20.015.6290643866914161616
21.012.9358855347320831313
22.010.302760430836571010
23.07.71668181343870488
24.05.16550407276872855
25.02.637705948321851733
26.00.1221773457406596700
Maximum ErrorAverage ErrorRoot mean square
0.45588373779138890.234581706936374760.27311676642511934

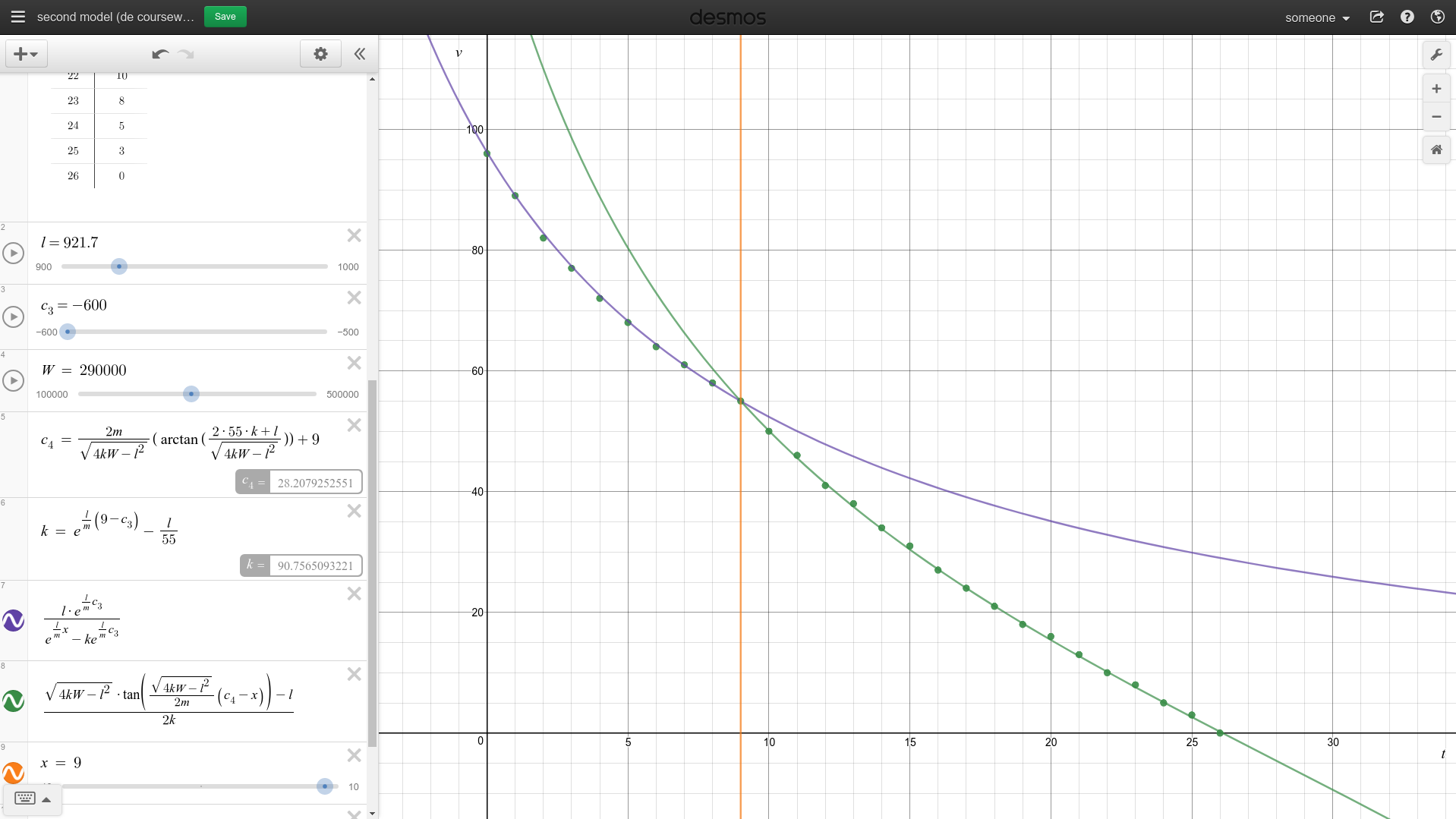
I’ll now look at the two configurations that I obtained and plot them. The red line shows the worst configuration, and the green line shows the best configuration.

./img/second_model_graph_result.png

As you can see in second_model_code_result rounded predictions of the best configuration exactly match the given data.

Conclusion of Model 2

\begin{equation} \begin{cases} v = \frac{λ e\frac{λ{m} c_3}}{e\frac{λ{m} t} - ke\frac{λ{m}c_3}}, & t ∈ [0, 9]
v = \frac{\sqrt{4kW - λ^2}tan(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - t)) - λ}{2k}, & t ∈ [9, 26] \ λ = 40.30628634043052 \ c_3 = -13809.4625600176 \ k = 102.95908302098627 \ W = 301557.65216452937 \ c_4 = 26.126510013890694 \ \end{cases} \end{equation}

$$ x = ∫_026 v dt = ∫_0^9 v dt + ∫_926 v dt $$ $$ v_1 = \frac{λ e\frac{λ{m} c_3}}{e\frac{λ{m} t} - ke\frac{λ{m}c_3}} = \frac{λ e\frac{λ{m} (c_3 - t)}}{1 - ke\frac{λ{m}(c_3 - t)}} = \frac{\frac{λ}{k} - \frac{λ}{k} + λ e\frac{λ{m} (c_3 - t)}}{1 - ke\frac{λ{m}(c_3 - t)}} = \frac{\frac{λ}{k}}{1 - ke\frac{λ{m}(c_3 - t)}} - \frac{\frac{λ}{k} - λ e\frac{λ{m} (c_3 - t)}}{1 - ke\frac{λ{m}(c_3 - t)}} = \frac{\frac{λ}{k}}{1 - ke\frac{λ{m}(c_3 - t)}} - \frac{λ}{k} $$ $$ ⇒ ∫ v_1 dt = \frac{λ}{k} (\frac{m}{λ} ∫ \frac{\frac{λ}{m}e\frac{λ{m}(t - c_3)}}{e\frac{λ{m}(t - c_3)} - k} dt - ∫ 1 dt) = \frac{mln(e\frac{λ{m}(t - c_3)} - k) - λ t}{k} + \mbox{constant} $$ $$ v_2 = \frac{\sqrt{4kW - λ^2}tan(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - t)) - λ}{2k} = \frac{1}{2k}(\sqrt{4kW - λ^2}tan(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - t)) - λ) $$ $$ \mbox{Let } u = \frac{\sqrt{4kW-λ^2}}{2m}(c_4 - t) $$ $$ ⇒ u’_t = -\frac{\sqrt{4kW-λ^2}}{2m} $$ $$ ⇒ ∫ v_2 dt = \frac{1}{2k} \left(\sqrt{4kW - λ^2} × (-\frac{2m}{\sqrt{4kW-λ^2}}) ∫ tan(u) du - ∫ λ dt\right) $$ $$ ⇒ ∫ v_2 dt = \frac{1}{2k} \left(2m ∫ \frac{-sin u}{cos u} du - λ ∫ dt\right) = \frac{2mln(cos(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - t))) - λ t}{2k} + \mbox{constant} $$

$$ ⇒ x = \left[\frac{mln(e\frac{λ{m}(t - c_3)} - k) - λ t}{k}\right]_0^9 + \left[\frac{2mln(cos(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - t))) - λ t}{2k}\right]_926 $$ $$ ⇒ x = \frac{1}{k} \left(\left[mln(e\frac{λ{m}(t - c_3)} - k)\right]_0^9 + \left[mln(cos(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - t)))\right]_926 - (13λ + 4.5λ)\right) $$ $$ ⇒ x = \frac{m}{k} (ln\left(\frac{e\frac{λ{m}(9 - c_3)} - k}{e\frac{λ{m}(- c_3)} - k}\right) + ln\left(\frac{cos(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - 26))}{cos(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - 9))}\right)) - 17.5\frac{λ}{k} $$ $$ ⇒ x = \frac{m}{k} ln\left(\frac{e\frac{λ{m}(9 - c_3)} - k}{e\frac{λ{m}(- c_3)} - k} × \frac{cos(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - 26))}{cos(\frac{\sqrt{4kW-λ^2}}{2m}(c_4 - 9))}\right) - 17.5\frac{λ}{k} $$

./img/second_model_integral.png

$$ ⇒ x ≈ 1057.8652498929307 ≈ 1060 $$

As you can see the value of $x$ is approximately equal to the one found from the first model, so recommendations are the same.

Assessment of the improvement obtained

Prediction

Based on the models I predict that the aeroplane stopped in $1060$ meters. The length of runway that I recommend is $2000$ meters for the reasons stated in the work.

Comparing the models

TimePredictedPredictedObservedBetter
SpeedSpeedSpeedModel
(1st Model)(2nd Model)
0.096.096.0000000000054961st
1.088.6567164179104588.66582512227822892nd
2.082.3570190641247882.37077686914407821st
3.076.8932038834951576.90862555559508772nd
4.072.109256449165472.12432763292139721st
5.067.8857142857142967.89907302369585682nd
6.064.1295546558704564.14028474770049641st
7.060.76726342710997460.77475738769026612nd
8.057.73997569866341557.743842139329196582nd
9.054.9999999999999955.00000000000179551st
10.050.1081665885211150.10157524003789502nd
11.045.62206303621237445.60871998373162462nd
12.041.47598886269637641.45588373779139412nd
13.037.6165993073075337.5898231332195381st
14.034.0000206230815533.96673336319917341st
15.030.58972451391777330.550133354391157311st
16.027.3549365175437827.309281417030515272nd
17.024.26942605339441524.217970303658813242nd
18.021.310573178346121.253597490201017212nd
19.018.4586384157813318.396437545757497182nd
20.015.69618312109478215.629064386691416161st
21.013.0076022774188512.935885534732083131st
22.010.37874161525026110.30276043083657102nd
23.07.7965779496973437.71668181343870481st
24.05.2489465589561615.16550407276872852nd
25.02.72430289862494132.637705948321851731st
26.00.21150836304155220.1221773457406596702nd
ModelMaximum ErrorAverage ErrorRoot mean squareNum. of better
predictions
1st0.475988862696375750.238224247534967070.277687510491139312
2nd0.45588373779138890.234581706936374760.2731167664251193415

Here is a graph of both of the models. The purple line is the first model and the green line is the second one.

./img/comparison_graph.png

The curves are so close to each other that at this scale you can’t even see the difference. The second model gave more accurate predictions, but the increase in accuracy is very small and the increases in complexity and computation time are significant.

About

A-level Differential Equations Airplane landing modelling coursework

Languages

Language:Haskell 100.0%