腾讯&字节&阿里：介绍一下快排原理以及时间复杂度，并实现一个快排

[瓶子君]

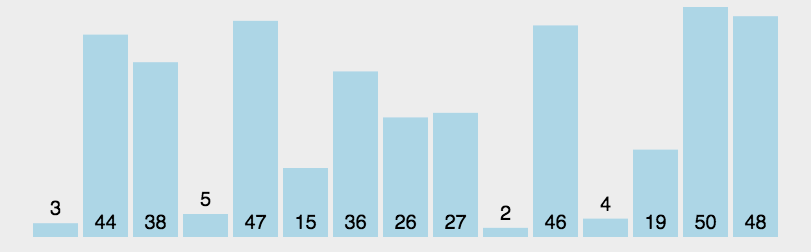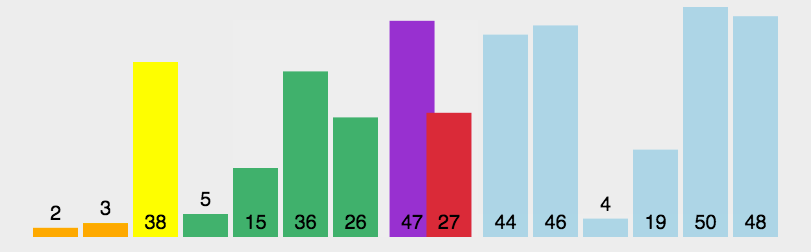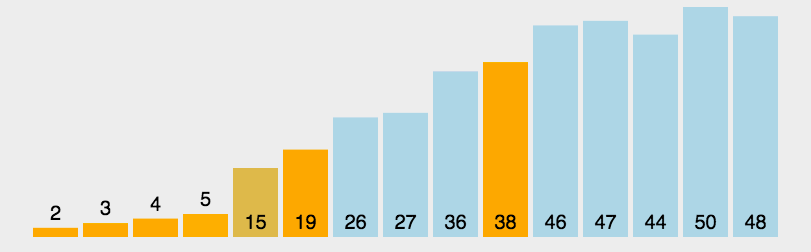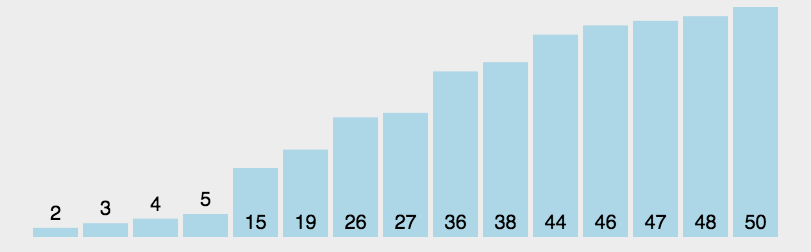
快排使用了分治策略的**，所谓分治，顾名思义，就是分而治之，将一个复杂的问题，分成两个或多个相似的子问题，在把子问题分成更小的子问题，直到更小的子问题可以简单求解，求解子问题，则原问题的解则为子问题解的合并。

快排的过程简单的说只有三步：

• 首先从序列中选取一个数作为基准数
• 将比这个数大的数全部放到它的右边，把小于或者等于它的数全部放到它的左边 （一次快排 partition）
• 然后分别对基准的左右两边重复以上的操作，直到数组完全排序

具体按以下步骤实现：

• 1，创建两个指针分别指向数组的最左端以及最右端
• 2，在数组中任意取出一个元素作为基准
• 3，左指针开始向右移动，遇到比基准大的停止
• 4，右指针开始向左移动，遇到比基准小的元素停止，交换左右指针所指向的元素
• 5，重复3，4，直到左指针超过右指针，此时，比基准小的值就都会放在基准的左边，比基准大的值会出现在基准的右边
• 6，然后分别对基准的左右两边重复以上的操作，直到数组完全排序

注意这里的基准该如何选择喃？最简单的一种做法是每次都是选择最左边的元素作为基准：

但这对几乎已经有序的序列来说，并不是最好的选择，它将会导致算法的最坏表现。还有一种做法，就是选择中间的数或通过 Math.random() 来随机选取一个数作为基准，下面的代码实现就是以随机数作为基准。

代码实现

let quickSort = (arr) => {
  quick(arr, 0 , arr.length - 1)
}

let quick = (arr, left, right) => {
  let index
  if(left < right) {
    // 划分数组
    index = partition(arr, left, right)
    if(left < index - 1) {
      quick(arr, left, index - 1)
    }
    if(index < right) {
      quick(arr, index, right)
    }
  }
}

// 一次快排
let partition = (arr, left, right) => {
  // 取中间项为基准
  var datum = arr[Math.floor(Math.random() * (right - left + 1)) + left],
      i = left,
      j = right
  // 开始调整
  while(i <= j) {
    
    // 左指针右移
    while(arr[i] < datum) {
      i++
    }
    
    // 右指针左移
    while(arr[j] > datum) {
      j--
    }
    
    // 交换
    if(i <= j) {
      swap(arr, i, j)
      i += 1
      j -= 1
    }
  }
  return i
}

// 交换
let swap = (arr, i , j) => {
    let temp = arr[i]
    arr[i] = arr[j]
    arr[j] = temp
}

// 测试
let arr = [1, 3, 2, 5, 4]
quickSort(arr)
console.log(arr) // [1, 2, 3, 4, 5]
// 第 2 个最大值
console.log(arr[arr.length - 2])  // 4

快排是从小到大排序，所以第 k 个最大值在 n-k 位置上

复杂度分析

• 时间复杂度：O(nlogn)
• 空间复杂度：O(nlogn)

[7777sea]

快排的原理是基于二分法的**，时间复杂度比较复杂，最好的情况是O(N)，最差的时候是O(N^2)，所以平时说的O(N*logN)为其平均时间复杂度。它的基本**是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

var quickSort = function(arr) {
  if (arr.length <= 1) { return arr; }
  var pivotIndex = Math.floor(arr.length / 2);
  var pivot = arr.splice(pivotIndex, 1)[0];
  var left = [];
  var right = [];
  for (var i = 0; i < arr.length; i++){
    if (arr[i] < pivot) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }
  return quickSort(left).concat([pivot], quickSort(right));
};

[jianqing]

快排的原理是基于二分法的**，时间复杂度比较复杂，最好的情况是O(N)，最差的时候是O(N^2)，所以平时说的O(N*logN)为其平均时间复杂度。它的基本**是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

var quickSort = function(arr) {
  if (arr.length <= 1) { return arr; }
  var pivotIndex = Math.floor(arr.length / 2);
  var pivot = arr.splice(pivotIndex, 1)[0];
  var left = [];
  var right = [];
  for (var i = 0; i < arr.length; i++){
    if (arr[i] < pivot) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }
  return quickSort(left).concat([pivot], quickSort(right));
};

这个比作者写的好，简单，容易理解。

嗯，作者你这个为啥要写这么复杂呢，理解起来也很难
.....刚刚发现这个写法是阮一峰老师的博客中的。。。

[JKCamus]

应该也算好理解吧

function quickSortRecursion(arr) {
  if (!arr || arr.length < 2) return arr;
  const pivot = arr.pop();
  let left = arr.filter((item) => item < pivot);
  let right = arr.filter((item) => item >= pivot);
  return [...quickSortRecursion(left), pivot, ...quickSortRecursion(right)];
}

[AAAngelina]

快排的原理是基于二分法的**，时间复杂度比较复杂，最好的情况是O(N)，最差的时候是O(N^2)，所以平时说的O(N*logN)为其平均时间复杂度。它的基本**是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

var quickSort = function(arr) {
  if (arr.length <= 1) { return arr; }
  var pivotIndex = Math.floor(arr.length / 2);
  var pivot = arr.splice(pivotIndex, 1)[0];
  var left = [];
  var right = [];
  for (var i = 0; i < arr.length; i++){
    if (arr[i] < pivot) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }
  return quickSort(left).concat([pivot], quickSort(right));
};

快排，什么时候是最好情况，时间复杂度为O（n）呢？

[gemmi]

快排的原理是基于二分法的**，时间复杂度比较复杂，最好的情况是O(N)，最差的时候是O(N^2)，所以平时说的O(N*logN)为其平均时间复杂度。它的基本**是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

var quickSort = function(arr) {
  if (arr.length <= 1) { return arr; }
  var pivotIndex = Math.floor(arr.length / 2);
  var pivot = arr.splice(pivotIndex, 1)[0];
  var left = [];
  var right = [];
  for (var i = 0; i < arr.length; i++){
    if (arr[i] < pivot) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }
  return quickSort(left).concat([pivot], quickSort(right));
};

这个比作者写的好，简单，容易理解。

嗯，作者你这个为啥要写这么复杂呢，理解起来也很难 .....刚刚发现这个写法是阮一峰老师的博客中的。。。

这个需要不断的新开数组，便于理解，但会有多余的时间和空间消耗，作者的版本是原地排序，没有多余的空间消耗，时间也更短。

[edte]

快排的原理是基于二分法的**，时间复杂度比较复杂，最好的情况是 O (N)，最差的时候是 O (N^2)，所以平时说的 ** O(N*logN) 为其平均时间复杂度。它的基本****是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

var quickSort = function(arr) {
  if (arr.length <= 1) { return arr; }
  var pivotIndex = Math.floor(arr.length / 2);
  var pivot = arr.splice(pivotIndex, 1)[0];
  var left = [];
  var right = [];
  for (var i = 0; i < arr.length; i++){
    if (arr[i] < pivot) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }
  return quickSort(left).concat([pivot], quickSort(right));
};

快排，什么时候是最好情况，时间复杂度为 O（n）呢？

已经排好序了就是 O(n)，完全逆序就会退化到 O(n^2)

[demo]

function quickSort(arr) {
    if (arr.length <= 1) {
      return arr;
    }
    let pindex = Math.floor(arr.length / 2)
    let m = arr.splice(pindex, 1)[0]
    let left = []
    let rigth = []
    let i = 0
    while (i < arr.length) {
      if (arr[i] < m) {
        left.push(arr[i])
      } else {
        rigth.push(arr[i])
      }
      i++

    }
    return quickSort(left).concat([m], quickSort(rigth));
  }