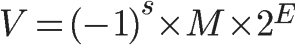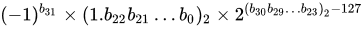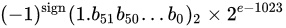JavaScript 浮点数运算的精度问题
pfan123 opened this issue · comments
JavaScript 浮点数运算的精度问题
在使用JS发现某些浮点数运算的时候,得到的结果存在精度问题:比如0.1 + 0.2 = 0.30000000000000004以及7 * 0.8 = 5.6000000000000005等等。
什么原因造成了这个问题?实际上是因为计算机内部的信息都是由二进制方式表示的,即0和1组成的各种编码,但由于某些浮点数没办法用二进制准确的表示出来,也就带来了一系列精度问题。当然这也不是JS独有的问题。
以0.1+0.2为例,理解浮点数的运算方法,如何规避这个问题。
计算机的运算方式
如何将小数转成二进制
**① 整数部分:**除2取余数,若商不为0则继续对它除2,当商为0时则将所有余数逆序排列;
**② 小数部分:**乘2取整数部分,若小数不为0则继续乘2,直至小数部分为0将取出的整数位正序排列。(若小数部分无法为零,根据有效位数要求取得相应数值,位数后一位0舍1入进行取舍)
利用上述方法,我们尝试一下将0.1转成二进制:
0.1 * 2 = 0.2 - - - - - - - - - - 取0
0.2 * 2 = 0.4 - - - - - - - - - - 取0
0.4 * 2 = 0.8 - - - - - - - - - - 取0
0.8 * 2 = 1.6 - - - - - - - - - - 取1
0.6 * 2 = 1.2 - - - - - - - - - - 取1
0.2 * 2 = 0.4 - - - - - - - - - - 取0
......
算到这就会发现小数部分再怎么继续乘都不会等于0,所以二进制是没办法精确表示0.1的。
那么0.1的二进制表示是:0.000110011......0011...... (0011无限循环)
而0.2的二进制表示则是:0.00110011......0011...... (0011无限循环)
而具体应该保存多少位数,则需要根据使用的是什么标准来确定,也就是下一节所要讲到的内容。
IEEE 754 标准
IEEE 754 标准是IEEE二进位浮点数算术标准(IEEE Standard for Floating-Point Arithmetic)的标准编号。IEEE 754 标准规定了计算机程序设计环境中的二进制和十进制的浮点数自述的交换、算术格式以及方法。
根据IEEE 754标准,任意一个二进制浮点数都可以表示成以下形式:
S为数符,它表示浮点数的正负(0正1负);M为有效位(尾数);E为阶码,用移码表示,阶码的真值都被加上一个常数(偏移量)。
尾数部分M通常都是规格化表示的,即非"0"的尾数其第一位总是"1",而这一位也称隐藏位,因为存储时候这一位是会被省略的。比如保存1.0011时,只保存0011,等读取的时候才把第一位的1加上去,这样做相当于多保存了1位有效数字。
常用的浮点格式有:
① 单精度:
这是32位的浮点数,最高的1位是符号位S,后面的8位是指数E,剩下的23位为尾数(有效数字)M;
其真值为:
② 双精度:
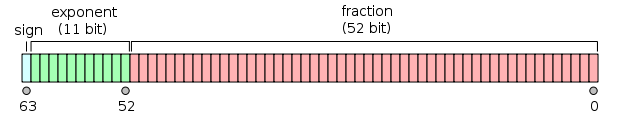
这是64位的浮点数,最高的1位是符号位S,后面的11位是指数E,剩下的52位为尾数(有效数字)M;
其真值为:
JavaScript只有一种数字类型number,而number使用的就是IEEE 754双精度浮点格式。依据上述规则,接下来我们就来看看JS是如何存储0.1和0.2的:
0.1是正数,所以符号位是0;
而其二进制位是0.000110011......0011...... (0011无限循环),进行规格化后为1.10011001......1001(1)*2^-4,根据0舍1入的规则,最后的值为
2^-4 * 1.1001100110011001100110011001100110011001100110011010
而指数E = -4 + 1023 = 1019
由此可得,JS中0.1的二进制存储格式为**(符号位用逗号分隔,指数位用分号分隔)**:
0,01111111011;1001100110011001100110011001100110011001100110011010
0.2则为:
0,01111111100;1001100110011001100110011001100110011001100110011010
***Q1:*指数位E(阶码)为何用移码表示?
***A1:*为了便于判断其大小。
浮点数运算
0.1 => 0,01111111011;1001100110011001100110011001100110011001100110011010
0.2 => 0,01111111100;1001100110011001100110011001100110011001100110011010
浮点数的加减运算按以下几步进行:
① 对阶,使两数的小数点位置对齐(也就是使两数的阶码相等)。
所以要先求阶差,阶小的尾数要根据阶差来右移**(尾数位移时可能会发生数丢失的情况,影响精度)**
因为0.1和0.2的阶码和尾数均为正数,所以它们的原码、反码及补码都是一样的。(使用补码进行运算,计算过程中使用双符号)
△阶差(补码) = 00,01111111011 - 00,01111111100 = 00,01111111011 + 11,10000000100 = 11,11111111111
由上可知△阶差为-1,也就是0.1的阶码比0.2的小,所以要把0.1的尾数右移1位,阶码加1(使0.1的阶码和0.2的一致)
最后0.1 => 0,01111111100;1100110011001100110011001100110011001100110011001101**(0)**
注:要注意0舍1入的原则。之所以右移一位,尾数补的是1,是因为隐藏位的数值为1(默认是不存储的,只有读取的时候才加上)
② 尾数求和
0.1100110011001100110011001100110011001100110011001101
+ 1.1001100110011001100110011001100110011001100110011010
——————————————————————————————
10.0110011001100110011001100110011001100110011001100111
③ 规格化
针对步骤②的结果,需要右规(即尾数右移1位,阶码加1)
sum = 0.1 + 0.2 = 0,01111111101;1.0011001100110011001100110011001100110011001100110011**(1)**
注:右规操作,可能会导致低位丢失,引起误差,造成精度问题。所以就需要步骤④的舍入操作
④ 舍入(0舍1入)
sum = 0,01111111101;1.0011001100110011001100110011001100110011001100110100
⑤ 溢出判断
根据阶码判断浮点运算是否溢出。而我们的阶码01111111101即不上溢,也不下溢。
至此,0.1+0.2的运算就已经结束了。接下来,我们一起来看看上面计算得到的结果,它的十进制数是多少。
<1> 先将它非规格化,得到二进制形式:
sum = 0.010011001100110011001100110011001100110011001100110100
<2> 再将其转成十进制
sum = 2^2 + 2^5 + 2^6 + ... + 2^52 = 0.30000000000000004440892098500626
现在你应该明白JS中 0.30000000000000004 这个结果怎么来的吧。
***Q2:*计算机运算为何要使用补码?
***A2:*可以简化计算机的运算步骤,且只用设加法器,如做减法时若能找到与负数等价的正数来代替该负数,就可以把减法操作用加法代替。而采用补码,就能达到这个效果。
浮点数精度问题的解决方法
- 调用round() 方法四舍五入或者toFixed() 方法保留指定的位数(对精度要求不高,可用这种方法)
- 将小数转为整数再做计算,即前文提到的那个简单的解决方案
- 使用特殊的进制数据类型,如前文提到的bignumber(对精度要求很高,可借助这些相关的类库)