Jumble Solver

Given a file with a list of words (e.g. this) and an English word, it will find all Jumble solutions for it, including substrings and anagrams.

Usage

python3 jumble.py [-h] word_list word

Positional arguments

word_list: File containing a list of words, one per line
word: Word used to find Jumble solutions

On this repository, there is an example word list file, from this repo.

Example

Using words.txt and dog as arguments, we get the following output:

$ python3 jumble.py words.txt dog
do
od
dg
gd
go
og
god

Implementation

As a reference for the time complexity, I've used this official Python page and these lecture notes. I've separated the code into the following parts:

main

Parses the arguments, calls the parse_word_list_file and jumble functions, then prints the result.

parse_word_list_file

Creates a jumble dictionary from a file containing a list of words. The keys of this dict are lowercase words with their letters sorted alphabetically, while the values are a list of original words. Storing the lowercase sorted words as the key ensures we will find anagrams with O(1) using Python dict.

jumble

Given the Jumble dict object and an input word, it will search for all jumble solutions for this word. Since we also want to search for substrings, it first finds the unique combinations of all letters for the input, from 2 to input word length. For each combination, we sort it and remove any whitespaces, then search on our jumble dictionary. If we find the sorted word on the jumble dict, we then merge the original words list our temporary dict object. We use it to avoid duplicates. The implementation of itertools.combinations returns unique combinations considering the position, not the value of the element. For example, the word "robot" would give the combination "ot" two times. However, as we will see in the Complexity Analysis section, the complexity of this code scales exponentially with the size of the input word, and the insertion on a dict is constant. So, in terms of time complexity, it is better to not remove the duplicates and let dict deal with the duplicates, because it has an O(1) index and store complexity.

Complexity analysis

Consider N the number of words on file and S the length of a word on that list. On parse_word_list_file function, we iterate over all words in file O(N) and run the following operations, with their respective complexity:

strip: O(S)
lower: O(S)
sorted: O(S log S)
setdefault: O(1)
append: O(1)

Thus, the complexity of parse_word_list_file function is:

O(N) * (O(S) + O(S) + O(S log S) + O(1)) = O(N * (2S + S log S + 1)) = O(2NS + NS log S + N) = O(NS log S)

Assuming that we are reading a list of words in English, and the average word length in English is 4.7, we could then replace S by 5:

O(N 5 log 5) = O(N)

On jumble, consider L the length of the input word, R the combination size, N the number of words from the input file, and C() the choose operator. Then, we do the following operations:

Loop R from 2 to input word length: so O(L-1) = O(L)
- Find the combinations, and iterate over their result: O(C(L, R) * R)
  - For each combination, we lower and sort, worst case it has length L: O(L) + O(L log L)
  - Then we search for the word on the jumble dict: O(1)
  - Append the result to another list: O(1)

Thus, the final complexity of jumble is O(L) * O(C(L, R) * R) * (O(L log L) + O(L) + O(1) + O(1))). But, from R=1 to L, the complexity of O(L) * O(C(L, R) * R) is O(2^L -1), and from R=2 to L, O(2^L-L-1) = O(2^L). Then, simplifying the complexity of jumble, we get: O(2^L) * (O(L log L) + O(L) + O(1) + O(1)) = O(2^L * L log L)

On main, we iterate over the results from jumble and print. In the worst case, we have all words from the initial file, so for printing the results we would have an O(N) complexity. Finally, adding main, jumble, and parse_word_list_file complexities, we get:

O(N) + O(N) + O(2^L * L log L) = O(N) + O(2^L * L log L)

Experiments

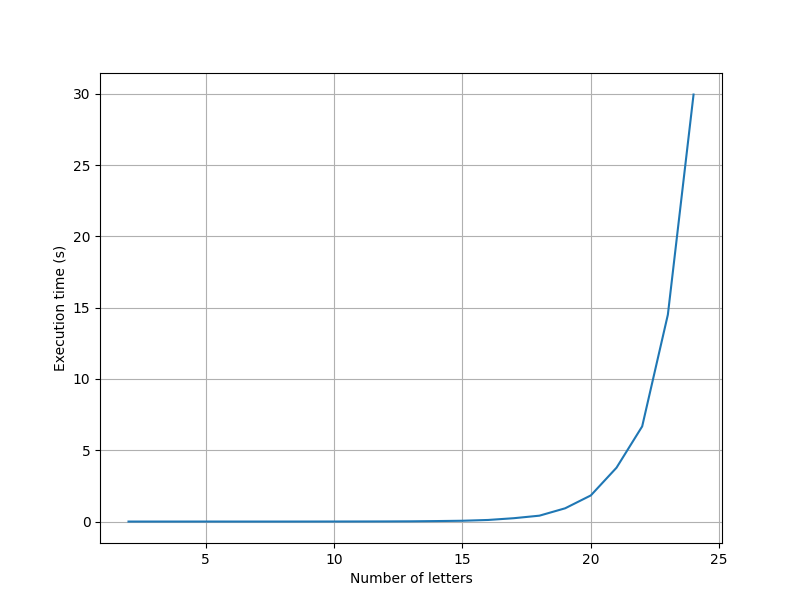
To evaluate this result, I've prepared the script complexity_experiment.py, which runs the jumble function with a list of words with an increasing number of letters. The following figure shows the execution time in seconds on Y-axis against the number of letters in the X-axis. We can see the exponential behavior on execution time, as we found in section Complexity analysis.

Unit tests

To test this software and allow a safe improvement of its performance without breaking the initial requirements, I used the Python built-in library unittest to implement tests. To run them, execute the following command from the project directory:

python3 -m unittest tests.tests.JumbleTests

lucascoelhof / jumble_solver_python