- Syntax: How do you write a language constructs?
- Semantics: what do programs mean? (Type checking, evaluation rules)
- Idioms: What are typical patterns for using language features to express your computation?
- Libraries: What facilites does the language (or a third-party project) provide as "standard"? (e.g., file access, data structures)
- Tools: What do language implementations provide to make your job easier? (e.g., top-level, debugger, GUI editor, ...)
- All are essential for good programmers to understand
- Breaking a new Programming Language down into these pieces makes it easier to learn.
We focus on semantics and idioms for OCaml
- Semantics is like a meta-tool: it will help you learn languages
- Idioms will make you a better programmer in those languages
Libraries and tools are secondary focus: throughout your career you'll learn new ones on the job every year
Syntax is almost always boring
- A fact to learn, like "Cornell was founded in 1865"
- People obsess over subjective preferences {yawn}
- Class rule: We don't complain about syntax
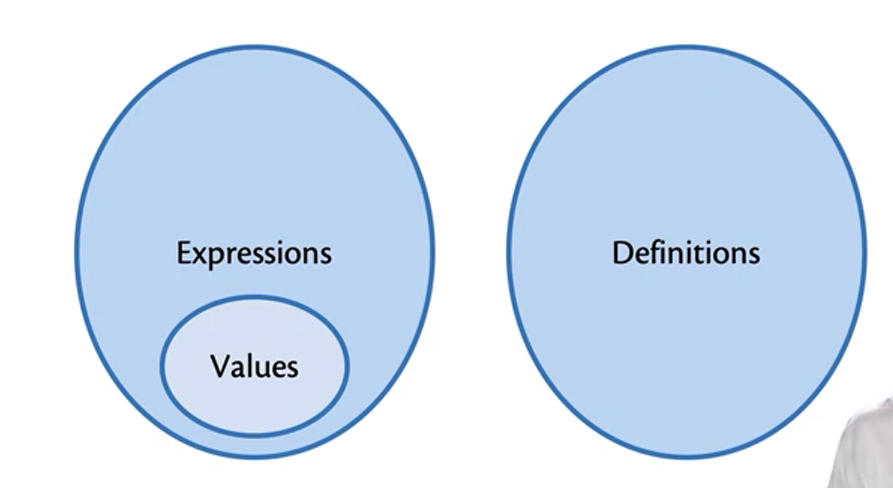
- Primary building block of OCaml programs
- Akin to statements or commands in imperative languages
Every kind of expression has: -> Syntax -> Semantics: -- Type-checking rules (static semantics): produce a type, or fail with an error message. -- Evaluation rules (dynamic semantics): produce a value, or exception or infinite loop
A value is an expression that does not need any further evaluation
-
OCaml compile infers types -- Compilation fails with type error if it can't -- Hard part of language design: guaranteeing compiler can infer types when program is correctly written
-
You can manually annotate type anywhere -- Replace e with (e: t) -- useful for diagnosing type errors
Syntax:
if e1 then e2 else e3
Evaluations:
1º: if e1 evaluates to TRUE, and if e2 evaluates to v (stands for a value "v"), then if e1 then e2 else e3 evaluates to v
2º: if e1 evaluates to FALSE, and if e3 evaluates to v, then if e1 then e2 else e3 evaluates to v.
Type checking: if e1 has type bool and e2 has type t and e3 has type t then if e1 then e2 else e3 has type t
if (e1 = bool) && (e2: T) && (e3: T) ==> T
if e1 : bool and e2 : t and e3 : t then if e1 then e2 else e3 : t
Evaluation:
1º case: if e1 ==> true and e2 ==> v, then (if e1 then e2 else e3) ==> v
2º case: if e1 ==> false and e3 ==> v, then (if e1 then e2 else e3) ==> v
type checking:
if e1 : bool and e2 : t and e3 : t
then (if e1 then e2 else e3) : t
input:
let x = 42;;
output:
val x : int = 42
what we are saying here reading right to left is:
let x = 42
val x : int = 42
results in a value 42
whose type was int
and was bound (vinculado) to the name x
A definition gives a name to a value
Definitions are not expressions, or vice-versa
But definitions syntactically contain expressions
Syntax:
let x = e where x is an indentifier
Evaluation:
- Evaluate e to a value v
- Bind (associate) v to x: henceforth, x will evaluate to v
under the hood: the is a memory location named x that contains v
the let definition is not an expression itself
example 1: let a = 0 in a;;
example 2: let b = 1 in 2 * b;;
example 3: let c = 3 in (let d = 4 in c + d)
example 4: let e = 5 in (let e = 6 in e);;
output:
- : int = 0
the "in" keyword that is making this a let expression as opposed to a let definition.
proving that isn't a definition because a isn't bound to anything.
let x = e
is implicitly, "in rest of what you type"
~~ in utop
e.g., you type:
let a = "big";;
let b = "red";;
let c = a^b;;
toplevel understands:
let a = "big" in
let b = "red" in
let c = a^b in
How to evaluate just
x
at toplevel?
Answer: substitution from that giant nested let expression
The Scope of a variable is where its name is meaningful
let x = 42 in
(* y is not meaningful here *)
x + (let y = "3110" in
(* y is meaningful here *)
int_of_string y)
let expressions give us the delimitation of scope inside an OCaml program
What does this mean?
let x = 5 in
((let x = 6 in x) + x)
It's darn confusing because of the overlapping scope:
we should avoid that in our own programs.
the name of a variable shouldn't intrinsically matter
e.g., in math, these are the same functions:
- f(x) = x + 1
- f(y) = y + 1
To ensure name irrelevance in programs, stop substituting when you reach a binding of the same name
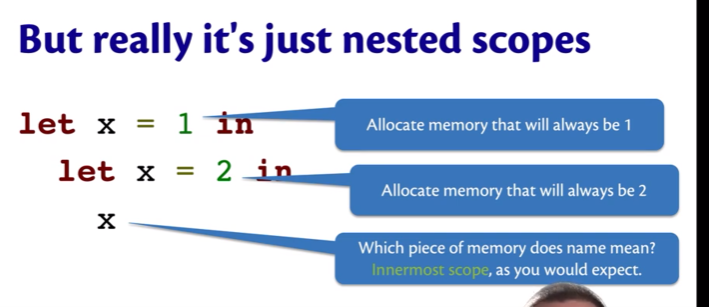
Seems like variable can mutate...
let x = 1;;
let x = 2;;
x;;
But really it's just nested scopes
let x = 1 in
let x = 2 in
x
(fun x -> x + 1);;
output:
- : int -> int = <fun>
another example:
(fun x -> x + 1) 3110;;
output:
- : int = 3111
It's anonymous function because isn't bounded to any name, and also this function receives an integer as argument and returns an integer.
the argument for this function was passed after parenthesis
Syntax:
fun x1 ... xn -> e
Evaluation:
- A function is a value: no further computation to do. just amazing.
- In particular body e is not evaluated until function is applied.
- Anonymous functions a.k.a lambda expressions.
- Math notation: λx . e
- The lambda means: "what follows in an anonymous function."
Can use them ANYWHERE we use value:
- Functions can take functions as arguments.
- Functions can return functions as results.
This is an incredible powerful language feature
Sytax:
e0 e1 ... en
No parentheses required. (unless you need to force particular order of evaluation)
Evaluation of
e0 e1 ... en
e0 ==> v0, ... en ==> vn
evaluating...
expression 0 ==> value 0
expression 1 ==> value 1
expression N ==> value N
fun x1 ... xn -> e
Evaluate it:
e' ==> v
Example 1:
(fun x -> x + 1) (2 + 3)
(fun x -> x + 1) 5 // here we already evaluated all the subexpressions
5 + 1 // here we substituted v1 for x1
6 // now this is our result
Eduardo once said: "It's about abtraction."
Another example:
(fun x y -> x - y) (3 * 1) (3 - 1) // here we evaluate all the subexpressions first
(fun x y -> x - y) ... (3 * 1) becomes 3 ... (3 - 1) becomes 2 // or just...
(fun x y -> x - y) 3 2 // now we have all the subexpressions evaluated to values.
3 - 2 // we must show the result...
1
i think i have exagerated on this example but it's for a good reason, i have to see in details and are we doing here.
let name = fun x -> x + 1;; // additional syntax with the 'fun' keyword
let name x = x + 1;; // it's the same but more beautiful.
the argument for the function goes right after it's name.
Syntactically different but SEMANTICALLY EQUIVALENT.
let inc = fun x -> x + 1
let inc x = x + 1
Note: both means the same thing.
Latter is SYNTATIC SUGAR.
- not necessary
- makes language "sweeter".
Another example:
(fun x -> x + 1) 2
let x = 2 in x + 1
Reassistir com atenção para tirar dúvidas: Named Functions | OCaml Programming | Chapter 2 Video 11
Must explicitly state that function is recursive:
let rec fact n =
if n = 0 then 1
else n * fact (n - 1)
Type t -> u is the type of a function that takes input of type t and return output of type u
Type t1 -> t2 -> u is the type of a function that takes input of type t1 and another input of type t2 and returns output of type u
etc.
Note dual purpose for -> syntax:
- Function types
- Function values
Type checking:
if
x1 : t1, ..., xn : tn
and
e : u
then
(fun x1 ... xn -> e) : (t1 -> ... -> tn -> u)
Poorly example:
(fun x1 -> e) : (t1 -> u)
Examples:
fun (x: int) -> x + 1
x + 1 : int
(fun x -> x + 1) : int -> int
--- Example 2 ---
fun x y -> x + y
x: int
y: int
(fun x y -> x + y)
: int -> int -> int
Type checking:
if e0 : t1 -> ... -> tn -> u
and e1 : t1 -> ... -> tn -> u
...,
en: tn
More syntatic sugar
Multi-argument functions do not exist
they just look like Multi-argument
but are really just syntatic sugar for single argument.
this:
fun x y -> e
if syntactic sugar for:
fun x -> (fun y -> e)
and also:
let add x y = x + y
is syntactic sugar for:
let add = fun x ->
fun y ->
x + y
again:
fun x y z -> e
is syntactic sugar for:
fun x -> (fun y -> (fun z -> e))
Can use them anywhere we use values:
- Functions can take functions as arguments
- Functions can return functions as results
This is an incredibly powerful language feature
Variable: name standing for unknown value Type variable: name standing for unknown type
Java example: List < T>
OCaml syntax: single quote followed by identifier.
e.g., 'foo, 'key, 'value
But most often simply just: 'a
Pronounced: "alpha"
- poly = many, morph = form
- Write function that works for many arguments regardless of their type
- closely related to Java generics
- also related to C++ template instantiation
- parametric polymorphism
Application:
let (@@) f x = f x
Reverse application
let (|>) x f = x f
a.k.a pipeline
Application operators can help you avoid having to write paretheses
[];;
output:
'a list = []
A list of elements of type alpha ('a)
[ [1; 2]; [3; 4]; [5; 6] ];;
output:
int list list = [[1; 2]; [3; 4]; [5; 6]]
- Immutable: can't change elements
- Singly-linked:
- Good for sequencial access of short-to-medium length lists (say, up to 10k elements)
- Data structures are tools: none is perfect.
Syntax: