Modeling the Distribution of Normal Data in Pre-Trained Deep Features for Anomaly Detection in PyTorch
PyTorch implementation of Modeling the Distribution of Normal Data in Pre-Trained Deep Features for Anomaly Detection.
This paper presents an anomaly detection approach that consists of fitting a multivariate Gaussian to normal data in the pre-trained deep feature representations, using Mahalanobis distance as anomaly score.
It is a simple yet effective approach and achieves SOTA on MVTec AD dataset.
- python 3.6+
- PyTorch 1.5+
- efficientnet_pytorch == 0.6.3
- sklearn, matplotlib
Install prerequisites with:
pip install -r requirements.txt
If you already download MVTec AD dataset, move a file to data/mvtec_anomaly_detection.tar.xz.
If you don't have a dataset file, it will be automatically downloaded during the code running.
To test this implementation code on MVTec AD dataset:
cd src
python main.py
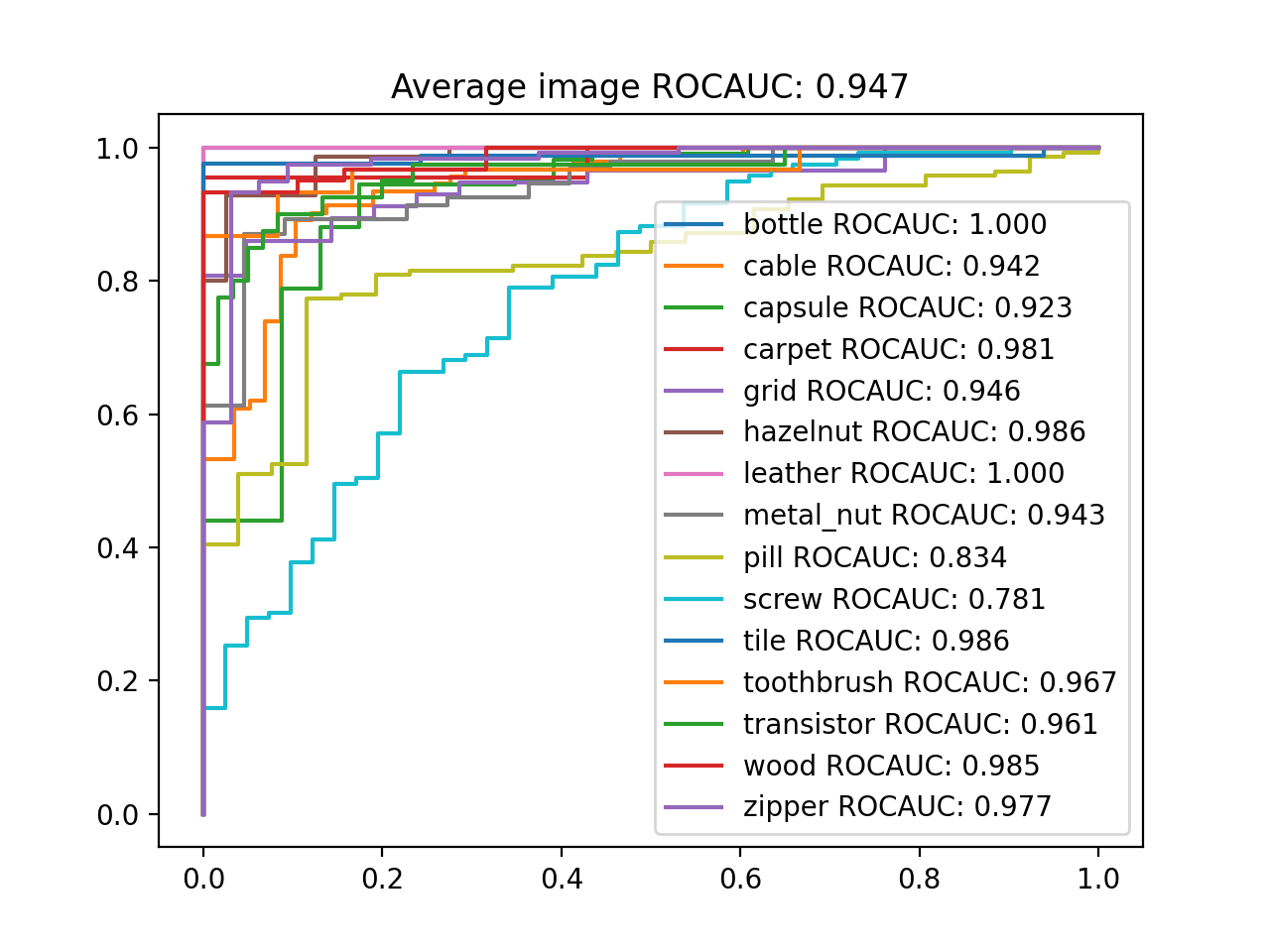
After running the code above, you can see the ROCAUC results in src/result/roc_curve_{model_name}.png
Below is the implementation result of the test set ROCAUC on the MVTec AD dataset.
| Paper | Implementation | |
|---|---|---|
| bottle | - | 100.0 |
| cable | - | 94.2 |
| capsule | - | 92.3 |
| carpet | - | 98.1 |
| grid | - | 94.6 |
| hazelnut | - | 98.6 |
| leather | - | 100.0 |
| metal_nut | - | 94.3 |
| pill | - | 83.4 |
| screw | - | 78.1 |
| tile | - | 98.6 |
| toothbrush | - | 96.7 |
| transistor | - | 96.1 |
| wood | - | 98.5 |
| zipper | - | 97.7 |
| Average | 94.8 | 94.7 |